Before Review
요즘 제가 Transformer 관련 논문을 많이 읽고 있습니다.
이번 논문도 Video Transformer를 위한 Self-Supervised Learning을 다룬 논문입니다.
리뷰 시작하도록 하겠습니다.
Introduction
Transformer 계열의 architecture들은 long-term dependency를 잘 capture 할 수 있다는 이유로 Video 진영에서 21년쯤부터 계속 활발하게 연구가 진행되고 있습니다. 3D Convolution은 제한된 Receptive Field 때문에 global information을 capture 하기에는 한계가 있습니다.
Transformer는 더군다나 입력의 길이에는 제한을 받지 않습니다. Transformer Encoder에는 몇 개의 token이든 다 입력으로 처리할 수 있으며, 사전학습 때 만든 positional encoding을 inference 단계에서는 interpolation을 하면 되기 때문입니다. 구조적으로 Transformer 자체는 확실히 long-term dependecny 만큼은 잘 해결할 수 있을 것 같습니다.
하지만 저자는 현재의 Video Transformer는 temporal dynamics에 집중을 하는 것이 아니라, spatial dynamics에 집중을 한다는 것을 주장합니다. 구조적으로는 temporal dynamics에 더욱 잘 집중할 수 있도록 설계가 되어있지만 정작 spatial dynamics 즉, local information에 집중한다는 의미입니다.
저자는 최근 Video Transformer 들이 때때로 입력 비디오의 temporal order가 shuffle 되어도 action recognition을 잘 수행한다는 observation을 얻습니다. 이는 temporal order는 상관없이 모델이 다른 곳에 집중을 하기 때문에 발생하는 것이겠죠.
따라서 저자는 기존의 Transformer 구조들이 temporal dynamics를 잘 capture 하지 못한다는 insight를 얻고 이를 보완할 수 있는 학습 방법을 고안합니다.
굉장히 간단한 두가지 task를 제안합니다. Temporal order와 Temporal flow를 기반으로 Self-Supervised Learning을 제안합니다. 자세한 얘기는 뒤에서 하고 제안되는 방법은 굉장히 간단해서 다른 SoTA 논문들에도 쉽게 적용할 수 있다고 합니다. 심지어 이미지 도메인에서도 적용할 수 있다고 합니다.
이미지 도메인에서는 foreground와 background 중 background를 debias 하는 방식으로 작동한다고 하네요.
Motivation : Bias toward Spatial Dynamics
Preliminaries
Video Transformers
$x=[x_{1},\ldots , x_{T}]\in \mathbb{R}^{T\times H\times W\times C}$를 비디오로 정의하면 $ T $ 번째 frame의 해상도는 $(H, W)$가 되며 채널은 $ C $가 되겠네요.
Video Transformer는 입력 $ x $을 $ hwt $ 개의 토큰의 sequence $\{ x^{(i)}\in \mathbb{R}^{\left( T/t\right) \times (H/h)\times \left( W/w\right) \times C}\}^{hwt}_{i=1} $로 다룹니다.
그리고 token 들은 linearly transformation 되며 $ D $ 차원의 positional embedding이 더해집니다.
- $ e^{(i)}=Ex^{(i)}+E^{(i)}_{pos}\in \mathbb{R}^{D}$
그리고 보통 Video Transformer는 $CLS$ 토큰을 사용하여 sequence token 전체를 대표합니다. 따라서 정리하면 입력 비디오 $ x $에 대해 전체 입력 sequence는 아래와 같습니다.
- $ e=[e^{[CLS]};e^{(1,1)};e^{(1,2)};\ldots ;e^{(s, t)}], where s=hw $
그리고 Video Transformer들은 이 입력 sequence $ e $에 대해서 동일한 차원을 가지는 output을 만들어내는데 이 과정에서는 spatial-temporal attention module이 사용이 됩니다.
Spatio-temporal attentions
Spatio-temporal attention은 self-attention의 연장선입니다. Attention 연산을 space와 time 축에 대해서 parallel 하게 진행하는 것이죠.
비디오 입력 $ e\in \mathbb{R}^{st\times D}$에 대해서 joint spatio-temporal attention은 아래와 같습니다.

그냥 self-attention과 동일합니다.
자 그럼 joint spatio-temporal attention의 연산 복잡도는 얼마나 될까요?
일단 token이 $ st $가 있습니다. 하나의 token에 대해서 attention weight를 계산하기 위해 space-time에 해당하는 token을 모두 봐야 하는 $ st $의 token과 연산을 진행해야 합니다.
전체 token이 $ st $ 개 있고 하나의 token당 $ st $ 번의 연산이 들어가기 때문에 모든 token을 처리하면 $ O(s^{2} t^{2})$의 복잡도를 가집니다. 이러한 문제점을 해결하기 위해 Timesformer는 divided attention을 제안합니다.
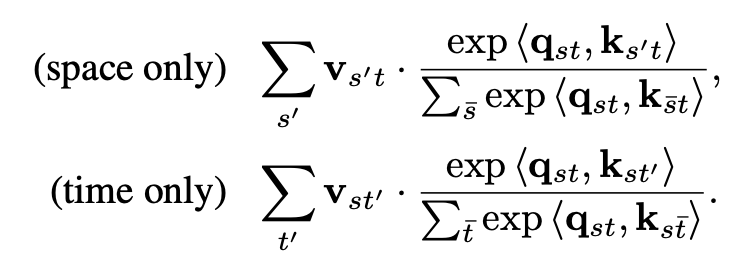
attention을 두 번 합니다. 한 번은 space 축에 대해서 그리고 한번은 time 축에 대해서 따로 진행하는 것이죠. 그럼 복잡도가 $ O(st^{2})+O(s^{2} t)$로 굉장히 낮아집니다. 약간 2D convolution을 1D + 1D로 진행하는 것과 비슷하다고 보시면 됩니다.
말이 조금 길어졌는데 정리해서 $ f_{\theta }$를 $\theta $에 의해 parameterized 된 전반적인 과정이라 정리하겠습니다.

$ f^{[CLS]}_{\theta }(x)$와 $f^{(i,j)}_{\theta }(x)$는 각각 $ CLS $ token과 $(i, j)$ 번째 token이라 정의하겠습니다.
그리고 $f^{[CLS]}_{\theta }(x)$이 보통 action recognition과 같은 down-stream task에 사용되는 representation이라 보시면 됩니다.
Observations
이제는 저자가 발견한 경험적인 observation에 대해서 다룹니다.
최근 Video Transformer 연구인 TimeSformer나 Motionformer와 같은 연구들이 SSv2라는 데이터셋에 대해서 action recognition을 할 때 temporal information을 exploit 할 때 굉장히 어려워하는 것을 발견했습니다.
Spurious correlation on spatial dynamics
첫 번째 oberservation은 temporal dynamics에 변화를 주어도 Video Transformer의 low confident에 영향을 주지 않는다는 것이죠. 일반적으로 모델이 temporal dynamics를 활용해 예측을 잘 수행하도록 학습이 되었다면 temporal order가 변화했을 때 예츠값이 많이 영향을 받아야 하는데 그렇지 않다는 것이죠.
이러한 경향성을 확인하기 위해 저자는 SSv2 test data에 대해서 Video Transformer 들에게 original video와 temporally shuffled video를 입력으로 넣어줍니다.
$ x $가 original video이고 $\tilde {x} $가 shuffled video입니다.

제가 보기에는 사실 좀 많이 떨어지는 것 같긴 한데... 저자는 TimeSformer-L을 기준으로 62.0->55.1이 되기 때문에 엄청 많은 drop은 아니다고 주장합니다. 무튼 이러한 결과는 모델이 temporal dynamics가 아닌 spatial dynamics에 집중한다는 것을 나타냅니다.
Vanishing temporal information
아래의 그래프를 보도록 하겠습니다.

x축은 block의 깊이입니다. 클수록 더 deep 한 layer라 보면 됩니다. y축은 Temporal Order Prediction Task에 대한 정확도입니다. 결과는 layer가 더 깊어질수록 모델은 temporal information을 잃고 있다고 볼 수 있겠네요.
이러한 발견을 토대로 temporal self-supervised task를 제안하게 됩니다.
TIME : Temporal Self-supervision for Video
위에서 얘기한 motivation을 토대로 저자는 Time Is MattEr(TIME)이라는 구조를 제안합니다. 전체적인 구조를 아래와 같습니다.

Debiasing spatial dynamics
그림을 보면 Original Video와 Shuffled Video를 동시에 입력으로 넣어주고 있습니다. Random shuffling 된 입력에 대해서는 높은 confidence를 가지고 싶지 않으니 아래와 같은 Loss를 설계합니다.
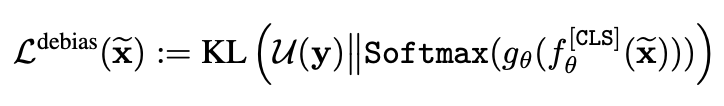
KL divergence의 형태입니다. 여기서 $ u(y)$는 uniform distribution입니다.
결국 shuffled video $\tilde {x} $에 대한 softmax 분포가 특정 곳에 bias 되는 것이 아니라 그냥 uniform 하게, 전반적으로 low confidence를 가지게 하기 위해 만들어진 loss입니다.
Learning temporal order of frames
아까 위에서 layer가 깊어질수록 temporal information을 잃는다고 했습니다. 따라서 가장 마지막 embedding을 가지고 temporal order prediction을 수행합니다.
여기서는 shuffled video를 사용하지 않고 original video를 가지고 prediction을 수행합니다.

$ y^{(j)}_{order}$는 간단합니다. 원래 $ t $ 번째 프레임이었다면 $ y^{(j)}_{order}=t $가 됩니다. 이렇게 cross-entropy loss를 가지고 temporal order classification을 수행할 수 있습니다.
Learning temporal flow direction of tokens
저자는 위의 loss만을 가지고는 temporal dynamic의 학습을 고도화할 수 없기에 temporal flow direction을 예측하는 task를 제안합니다. 논문에 적혀있는 내용 자체만 그대로 옮기자면 아래와 같습니다.
일단 인접한 두 프레임을 이용하여 optical flow를 만들어내고 이 flow의 direction을 예측하는 task가 진행됩니다.
- $\{ r^{(i, j)},\phi^{(i, j)} \} =Polar\left( Farneback\left( x_{j}, x_{j+1}\right) \right) $
일단 인접한 두 프레임을 가지고 Gunnar Farneback의 optical flow 알고리즘을 사용하여 flow를 만들고 이를 극좌표에 나타낸다고 합니다. 정확히 어떻게 수행되는 것인지는 잘 모르겠네요..
다음으로 $ y^{(i, j)}_{flow}$를 생성합니다.

optical flow의 magnitude가 일정 threshold를 넘은 flow에 대해서는 1~8까지의 정수값을 할당해 주는 방식입니다. 무슨 얘기냐면 $0\leq \phi^{(i, j)} <2\pi \rightarrow 1\leq \lfloor \phi^{(i, j)} \cdot \frac {4}{\pi } \rfloor +1\leq 8 $ 이렇게 되기 때문이죠.
그리고 인접한 프레임끼리의 임베딩을 아래와 같이 구해줍니다.

그리고 인접합 프레임끼리의 임베딩을 가지고 space 축에 대해서 attention module $ h $에 넣어 최종 임베딩을 얻어줍니다.

그리고 이 attention module을 통과하고 나온 임베딩을 가지고 flow loss를 계산합니다.
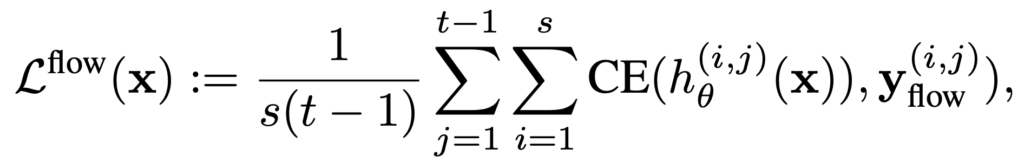
제가 Gunnar Farneback의 optical flow에 대한 이해도가 조금 부족하여 이 부분을 설명할 때 부족한 부분이 있을 것 같습니다...
핵심은 이러한 temporal flow의 direction을 예측하는 self-supervised task를 추가하여 더욱 temporal dynamcis에 집중하게 만들었다고 보시면 됩니다.
최종 Loss는 아래와 같습니다.
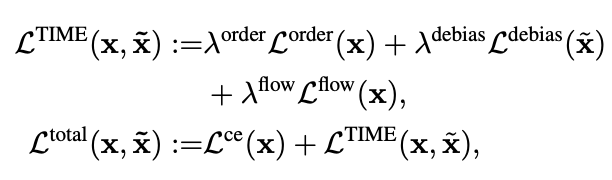
Experiments
Dataset
Dataset으로는 Something-to-Something version2(SSv2)를 사용했습니다. 저도 몰랐는데 SSv2 데이터셋에는 static class와 temporal class가 동시에 존재한다고 하네요.
보통 벤치마킹을 할 때 Kinetics를 사용하는데 Kinetics에는 temporal class가 별로 존재하지 않아 temporal modeling benchmark에 적합한 데이터셋은 아니라고 하여 저자는 SSv2만을 사용했다고 합니다.

Temporal Modeling on SSv2
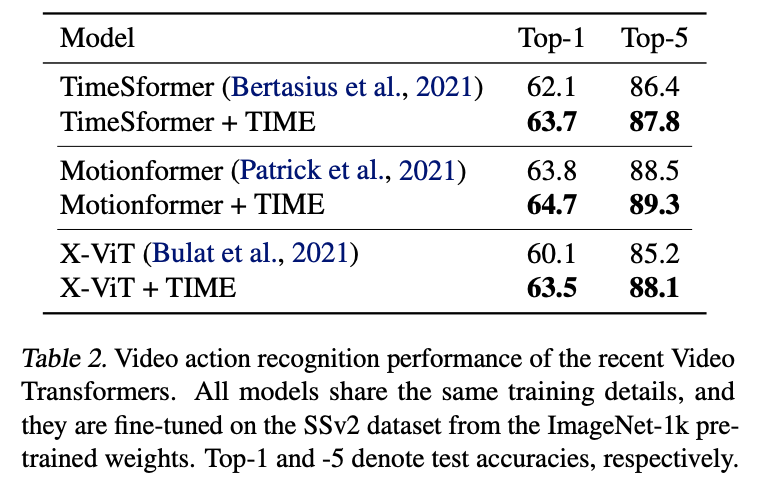
아래의 테이블을 보면 다른 Video Transformer Backbone에 TIME 학습 방식을 추가하면 모두 골고루 성능이 잘 오르는 것을 확인할 수 있습니다. 이 실험을 통해 TIME이 가지는 좋은 일반성과 확장성에 대해서 확인할 수 있을 것 같습니다.
Ablation Study
다음은 ablation study입니다.
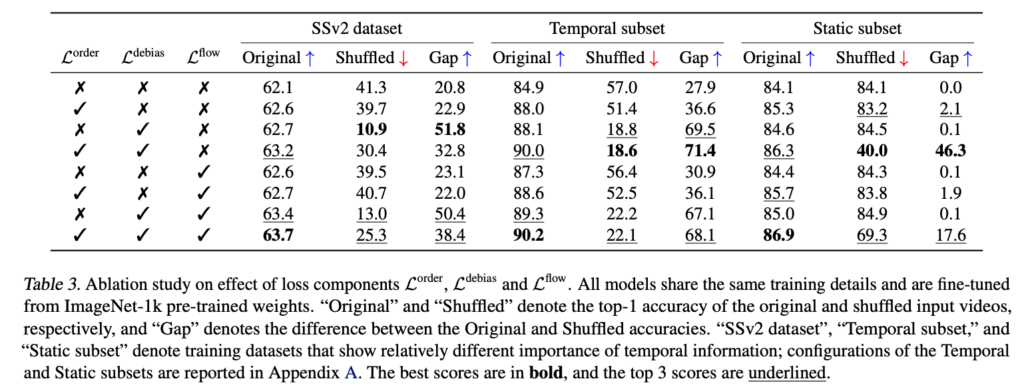
각각의 loss를 다시 한번 간단히 정리해 보도록 하겠습니다.
- $ L^{order}$ : temporal order을 예측하여 vanishing temporal dynamics를 방지하기 위함
- $ L^{debias}$ : spatial dynamics에만 집중하는 것을 방지하기 위함
- $ L^{flow}$ : temporal flow direction을 예측하여 temporal dynamics 학습을 더욱 강화하기 위함
우선 모든 loss를 다 사용하는 것이 가장 좋은 성능을 보여줌으로써 loss component들이 모두 상호보완적으로 작동함을 확인할 수 있습니다.
또한 제안되는 loss들은 특히 temporal subset 즉, temporal modeling을 요구로 하는 상황에서 더 작동하는 것을 볼 수 있습니다. static에 비해서 성능 향상폭이 더 크기 때문입니다.
Extension to image classification
저자가 제안하는 TIME의 아이디어를 image classification에서도 효과적인지에 대한 실험입니다.
- Image의 spatial order를 예측 ($ L_{I}^{order}$)
- Image의 background에 집중하는 spatial dynamics를 debiasing ($ L_{I}^{debias}$)
이렇게 하면 TIME의 아이디어를 그대로 이미지에 접목시켰다고 볼 수 있습니다.
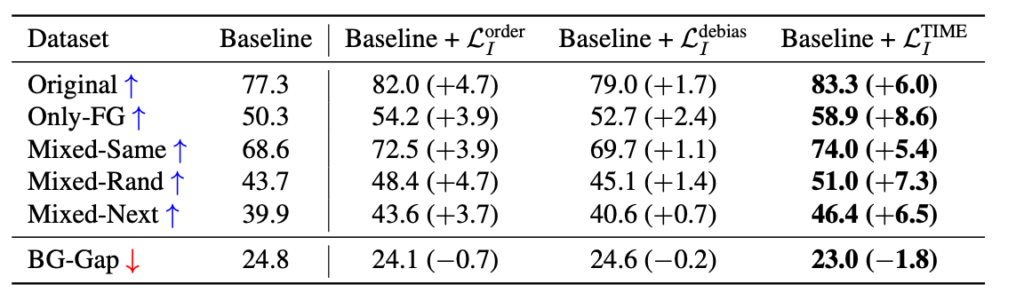
놀랍게도 이러한 방법이 이미지 도메인에서도 굉장히 잘 먹힌다는 것을 확인할 수 있습니다. 저도 자세히 아는 것은 아니지만 저기 Only-FG, Mixed-Same 등등이 다 하나의 Background Challenge Benchmark task라고 합니다.
모든 challenge에 대해서 굉장히 높은 성능 향상을 가져온 점을 보면 저자가 제안하는 방법의 우수함을 확인할 수 있을 것 같네요.
Conclusion
Transformer 구조가 long-term dependency를 잘 capture 할 수 있다고는 하지만 정작 Video Transformer는 temporal dynamics를 잘 사용하지 못한다는 아이러니한 점을 문제삼은 굉장히 좋은 연구인 것 같습니다.
결국 temporal information은 단순히 transformer를 쓴다고 해결되는 것이 아니라는 점을 깨닫게 해 준 논문인 것 같습니다.
이상으로 리뷰 마치도록 하겠습니다.



