Before Review
이번에도 BackBone 연구입니다. 흥미로웠던 것은 3D CNN의 장점과 Vision Transformer의 장점을 묶어 하나의 통합된(Unified) 구조를 제안하는 것이 인상 깊었습니다.
리뷰 시작하도록 하겠습니다.
Preliminaries
딥러닝에서 자주 활용되지만 따로 알아보지 않으면 낯선(?) 연산들에 대해서 알아보도록 하겠습니다.
Gaussian Error Linear Unit (GELU)
요즘 BERT나 GPT 그리고 ViT 기반의 최신 논문 혹은 MLP-Mixer와 같은 최신 연구에서 정말 자주 보이는 활성화 함수입니다. 저도 그냥 ReLU 보다 GELU가 더 좋더라 정도로만 알고 있었는데 GELU가 어떻게 formulation 되는지는 알아본 적이 없어 이번 기회에 정리하게 되었습니다. 논문을 읽기에는 Cost가 너무 커 잘 정리된 블로그 글을 참고하였습니다.
GELU 함수는 dropout이나 ReLU 함수의 특성을 골고루 섞어 정의되었습니다. 일단 ReLU 함수는 입력 값의 부호에 따라 deterministic 하게 1을 곱해주거나 0을 곱해주는 함수입니다. Dropout 같은 경우는 신경망 다발을 끊어주는 데 이는 stochastic 하게 1을 곱해주거나 0을 곱해준다고 볼 수 있겠네요.
이때 이러한 두 가지 성질을 조합하여 입력 값에 0 또는 1로 이루어진 값을 곱해주려고 하는데 이를 stochastic 하게 곱하면서도 stochasticity를 입력의 부호가 아닌 다른 값을 기준으로 정하고자 합니다. 구체적으로 입력값에 m∼Bernoulli(Φ(x))를 곱해줍니다.
그리고 이때 Φ(x)=P(X≤x),X∼N(0,1)의 형태로 가정을 합니다. 이는 표준화된 정규 분포의 누적 분포 함수의 형태죠. 표준 정규 분포를 가정하는 이유는 일반적으로 신경망에서 배치 정규화를 진행해 주니깐 표준 정규분포로 입력이 들어올 것을 가정하였다고 합니다. 누적 분포 함수 Φ(x)=P(X≤x)에서 x가 작아지면 P(X≤x)도 작아지니깐 x가 dropped 확률이 높아집니다.
입력 x 값이 작아질수록 drop 될 확률이 stochastic 하게 결정이 됩니다. 하지만 적어도 활성화 함수로 사용하기 위해서는 deterministic 하게 동작을 해야 하니 확률의 평균값으로 고정을 하면 되겠죠.
- Φ(x)×x+(1−Φ(x))×0=xΦ(x)
그리고 누적 분포 함수를 error 함수의 형태로 변경할 수 있다고 합니다.
- xΦ(x)=xP(X≤x)=x2[1+erf(x/√2)]
그리고 error 함수를 다시 아래의 형태로 근사할 수 있다고 합니다.
- 0.5x[1+tanh[√2/π(x+0.044715x3)]]

GELU는 위의 그림과 같은 형태로 생겼습니다. GELU의 누적 분포 함수를 정의할 때 정규 분포를 사용했는데 정규 분포의 분산을 0으로 보내면 ReLU가 되는 것을 보아 GELU는 ReLU의 smooth 함수 버전인 것 같습니다.
GELU 함수의 특징으로는 우선 모든 점에서 미분이 가능한 smooth 함수라는 점이며 단조 증가함수가 아니라는 점입니다. 단조 증가가 아니라는 것은 비선형성을 증가시키는 데에 더욱 도움이 될 수 있다고 볼 수 있죠.
또한 GELU는 입력 x가 다른 입력에 비해 얼마나 큰 지에 대한 상대적인 비율로 activation이 되기 때문에 확률적인 해석 역시 가능해진다고 합니다.
Depth-wise Convolution
Depth-wise Convolution이라고 해서 저도 주워듣다가 이번에 다시 알아보게 되었습니다. 아래 그림 먼저 보시면 일반적인 Convolution과 어떤 점이 다른지 바로 파악할 수 있습니다.

Standard Convolution은 Filter 별 Output을 따로 구분하지 않고 모두 더해주었지만 Depth-wise Convolution은 Filter 별로 나오는 Output을 그대로 Feature Map으로 사용합니다. Depth-wise Convolution은 주로 연산량을 줄여야 하는 상황에서 사용해주고 있습니다. 연산량이 얼마큼 줄어드는지 수치적으로 확인해보고 싶은 분은 잘 정리된 글이 있어 참고하시면 될 것 같습니다.
저는 일단 연산 자체가 어떻게 수행되는지 그리고 이렇게 연산을 하는 목적 정도로만 간략하게 설명하고 넘어가도록 하겠습니다.
3D Convolution
비디오 데이터는 프레임의 연속적인 변화를 바탕으로 스토리, 콘텐츠가 생성됩니다. 따라서 프레임과 프레임 사이의 연관 관계인 시간 정보, Temporal 한 Information도 중요하게 작용하게 됩니다. 시간 축에 대한 변화도 이해하기 위해 비디오 데이터는 시간 축으로도 Convolution filtering이 진행됩니다.
따라서 , 3D convolution filter는 축이 하나 늘어나게 됩니다. 바로 시간에 대한 축이고, frame과 frame 간의 정보를 받아오게 됩니다. 아래의 그림을 보면 조금 감이 오실 수 있는 데, 그림 (b)와 (c)의 차이를 주목해서 보시면 됩니다.

2D convolution
input data : (3, 16, 171, 128) = 3 채널이고(RGB), 16 frame으로 구성, resolution은 171 x 128
convolution filter dimension : (16, 3, 3) = 3 by 3의 kernel_size를 가지며 depth는 16
이때 2d convolution을 적용해 주면, 16 frame이 한꺼번에 연산이 진행되기 때문에 프레임간의 시간적인 feature를 효과적으로 추출할 수 없다고 합니다.
3D convolution
input data : (3, 16, 171, 128) = 3 채널이고(RGB), 16 frame으로 구성, resolution은 171 x 128
convolution filter dimension : (3, 3, 3) = 3 by 3의 kernel_size를 가지며 depth는 3
이때 3d convolution을 적용해 주면 , 16 frame을 세 개씩 살펴보면서(depth = 3) frame 방향으로도 stride 연산이 진행되며, 그림 (c)와 같은 방식으로 연산이 진행되게 됩니다.
2D conv는 multiple frame에 대해 적용해 주면 2차원 형식의 feature map이 생성되면서 temporal 한 information을 잃게 되지만, 3D conv는 multiple frame에 대해 적용해 주면 3차원 형식의 volume을 가지는 feature map이 생성되면서 temporal 한 정보를 유지할 수 있게 됩니다.
이와 같이 비디오에서는 spatio-temporal feature를 추출하기 위해 3D Convolution을 사용하기도 합니다.
Introduction
비디오 데이터는 high-dimensional 한 특징 때문에 풍부하고 다양한 spatio-temporal semantic information을 가지고 있습니다. 하지만 프레임간의 large local redundancy와 complex global dependency 때문에 위의 정보를 효과적으로 encoding 하기는 어렵습니다.
최근의 비디오 이해 연구들은 3D Convolution을 활용하거나 요즘 뜨고 있는 Vision Transformer를 많이 사용하곤 합니다. 이미지 도메인에서 Convolution과 Transformer가 많이 비교가 됩니다. 비디오 도메인에서도 두 연산의 차이로 인한 장단점이 발생합니다.
3D Convolution은 결국 3D locality를 가정하기 때문에 local context를 이해하는 데는 효과적일 수 있지만 제한된 receptive field로 인해 global dependency를 해결하기는 어려운 점이 있습니다.
Vision Transformer는 self-attention mechanism으로 인해 long-range dependency를 효과적으로 encoding 할 수 있습니다. 하지만 attention weight를 계산할 때 모든 token들이 관여되기 때문에 local redundancy를 해결하기에는 어려움이 있습니다.
아래의 그림은 21년도에 나온 TimeSformer의 attention을 시각화 한 그림입니다.

비교적 shallow layer인 Layer3의 Spatial Attention를 보면 비슷한 부분에서만 attention이 되는 것을 볼 수 있습니다. 인접한 프레임에서 비슷한 부분만 보면 메모리와 연산이 낭비된다고 볼 수가 있죠. Temporal Attention 역시 인접한 두 프레임에서만 크게 발생하고 나머지는 거의 무시된다고 볼 수 있습니다.
안 그래도 비디오 데이터 자체가 무거운 상황인데, 별로 필요 없는 연산도 많이 낭비가 되는 상황이라 저자는 이러한 computation-accuracy 관계를 효율적으로 해결하려고 합니다. 이를 위해 본 논문에서는 서로 상호 보완적으로 작용할 수 있는 Convolution과 Vision Transformer의 장점을 섞을 수 있는 구조를 제안합니다.
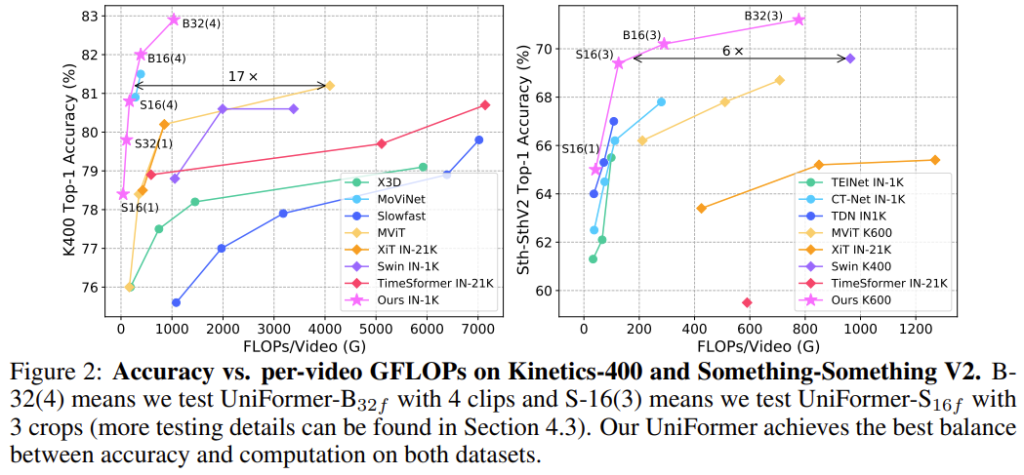
Video Classification 분야에서 Benchmarking에 사용되는 대표적인 두 데이터셋인 Kinetics와 Something-Something에서 기존 모델 대비 가장 좋은 accuracy-computation trade-off 관계를 보여줍니다. 뒤에 실험 섹션에서도 구체적인 FLOPs를 비교할 예정인데, 모델이 참 가벼우면서도 성능이 우수한 것이 대단한 것 같습니다.
Method
Overview of Uniformer Block
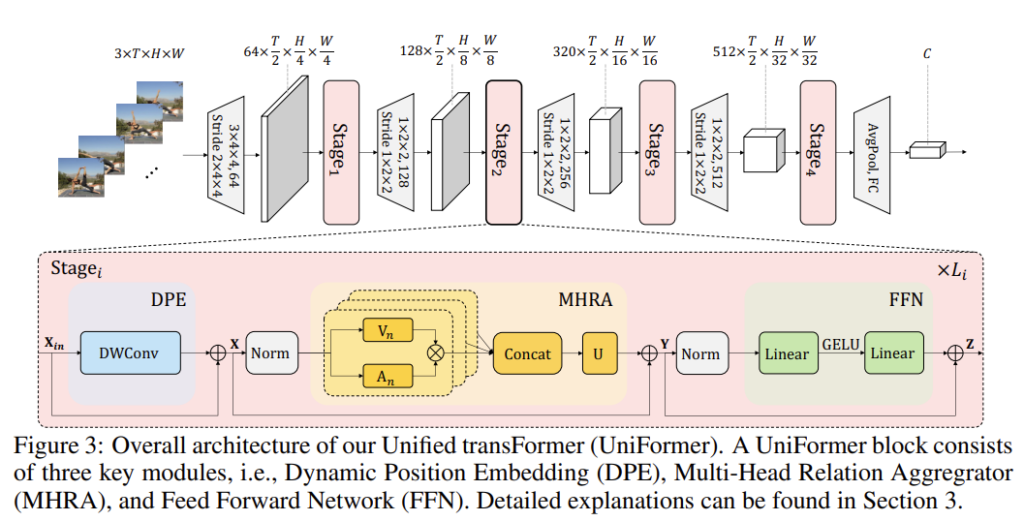
제안되는 Uniformer는 세 가지의 모듈로 구성되어 있습니다. 바로 Dynamic Position Embedding과 Multi-Head Relation Aggregator와 Feed-forward Network로 구성되어 있습니다.
Dynamic Position Embedding은 permutation-invariance 문제를 극복하여 좀 더 3D position 정보를 잘 통합할 수 있도록 고려되었다고 합니다.
Multi-Head Relation Aggregator는 기존의 Multi-Head Self Attention과는 다르게 모델의 shallow layer와 deep layer 간의 학습 방식의 차이를 두어 local video redundancy와 global video dependency를 효과적으로 처리할 수 있는 모듈입니다.
마지막으로 FFN은 각 token 끼리의 pointwise enhancement를 위한 두 개의 선형 레이어로 구성되어 있습니다.
여기서 Dynamic Position Embedding과 Feed-forward Network가 뭔가 거창한 것 같지만 사실 굉장히 간단하게 구성되어 있습니다. 논문의 가장 큰 contribution은 Multi-Head Relation Aggregator라 볼 수 있으니 이 부분에 집중하시면 될 것 같습니다.
Multi-Head Relation Aggregator
계속 위에서 강조했던 local redundancy와 global dependency 문제를 해결하기 위해서는 3D Convolution과 Vision Transformer를 동시에 활용해야 한다고 설명했습니다.
이를 위해 저자는 일단 Transformer의 format을 가지는 모델로 설계하되 shallow layer에서는 3D Convolution처럼 동작하고 deep layer에서는 Vision Transformer처럼 작동하는 구조를 제안합니다.
MHRA는 크게 아래와 같이 동작합니다.
- Rn(X)=AnVn(X)
- MHRA(X)=Concat(R1(X);R2(X);⋯;RN(X))U
일단 입력 비디오 텐서 X∈RC×T×H×W가 token sequence X∈RL×C로 처리가 됩니다. 이때 L=T×H×W이고, 이는 pixel 레벨에서 reshape만 해줬다고 보면 됩니다.
- Vn(⋅)은 Linear projection layer입니다. Original pixel token을 contextual token으로 변환해 주는 과정이며 Vn(X)∈RL×CN, channel 축이 CN으로 변환됩니다.
- An token affinity 즉, 토큰끼리의 유사도를 학습할 수 있는 Layer입니다. L개의 token 끼리의 유사도를 바탕으로 weight를 학습합니다. An∈RL×L 이 relation aggregator를 통해 token 끼리의 context를 요약하게 되고 이 부분이 RA를 통한 학습의 핵심이라 볼 수 있습니다.
- Rn(⋅)는 n 번째 head의 Relational Aggregator입니다. 그리고 U∈RC×C는 learnable matrix인데 N 개의 head를 integrate 해주는 역할을 합니다.
Local MHRA
저자는 shallow layer에서는 local spatiotemporal context를 통해 detailed video representation을 얻길 희망했습니다. 이를 위해 작은 3D block을 이용해 3D convolution처럼 작동될 수 있도록 Local MHRA를 제안합니다. Convolution이 shallow layer에서는 receptive field가 작아 detail 한 정보에 집중하는 것처럼 말이죠.
저자는 token affinity를 learnable parameter matrix로 제안합니다. 이때 연산은 모든 token이 아니라 local 3D neighborhood에서만 진행됩니다. 즉, shallow layer에서는 locality를 가정하는 것이죠.
하나의 anchor token Xi가 있다면 local MHRA는 small tube Ωt×h×w를 통해서 local spatiotemporal affinity를 학습합니다.
- Alocaln(Xi,Xj)=ai−jn,wherej∈Ωt×h×w
즉, 구조는 transformer 형식으로 가져가지만 attention 연산은 local 단위로 진행하겠다는 소리입니다. shallow layer에서는 천천히 변하는 비디오 프레임 사이의 미묘한 차이를 알아차리는데 도움이 되는 detail 한 정보에 집중을 할 수 있게 local operator를 설계했습니다.
Comparison to 3D Convolution Block
저자는 본인들이 설계한 local MHRA Block이 MobileNet Block의 spatiotemporal 한 확장 버전이라고 볼 수 있다 합니다.
일단 linear transformation V(⋅)은 point-wise convolution이라 볼 수 있습니다. point-wise convolution은 1×1 filter를 가지고 convolution을 하는 것입니다. point-wise convolution의 연산 과정을 잘 떠올려 보면 Linear Layer와 비슷합니다.
다음으로 relation aggregator Rn(X)=AlocalnVn(X)은 depth-wise convolution이라 볼 수 있습니다. 사실 이 부분이 이해가 잘 안 됐습니다. 그냥 convolution도 아닌 depth-wise convolution이랑 비슷하다고 한 걸 보면 뭔가 있는 거 같은데... 완전히 이해하려면 코드를 까봐야 할 것 같습니다.
뭔가 그래도 마지막으로 모든 head가 concat 된 다음에 linear matrix U로 합치는 과정은 point-wise convolution과 비슷합니다.
결과적으로 local MHRA는 PWConv - DWConv - PWConv의 형태로 정리할 수 있습니다. 그런데 PWConv-DWConv-PWConv의 형태는 Mobile Net에서 사용하는 형태로 연산량을 낮게 가져갈 수 있는 장점이 있습니다. 이러한 구조적 유사성 때문에 Uniformer 역시 연산량을 줄일 수 있었다고 하네요.
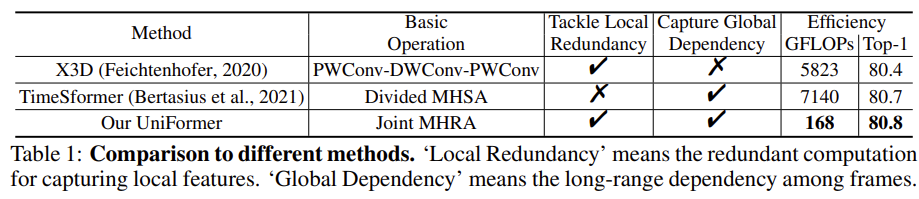
실제로 다른 Backbone 들이랑 GFLOPs를 비교하면 훨씬 낮은 것을 확인할 수 있습니다. 근데 여기서 궁금한 건 저기 보이는 X3D라는 녀석도 PWConv-DWConv-PWConv의 연산 구조를 가져가는데 GFLOPs는 또 왜 이렇게 차이가 나는지 궁금하네요. 디테일한 요소는 논문을 읽어보지 않으면 모르기 때문에 그냥 넘어가겠습니다.
Global MHRA
다음으로 저자는 deep layer에서는 long-term token dependency를 해결하고자 합니다. 사실 여기는 Transformer의 구조 그대로 가져가면 된다고 보시면 됩니다.
- Aglobaln(Xi,Xj)=eQn(Xi)TKn(Xj)∑k∈ΩT×H×WeQn(Xi)TKn(Xk)
위의 수식은 softmax 함수입니다. Xj는 global 3D tube에 있는 어떠한 token도 될 수 있습니다. Qn(⋅)과 Kn(⋅)은 각각 query, key를 생성하기 위한 다른 linear transformation입니다.
대부분의 video transformer 들은 self-attention 연산을 모든 stage에서 진행하기에 많은 computation을 가져간다고 합니다. Dot-product 연산을 줄이기 위해 이전의 work인 TimeSformer는 spatial temporal attention을 분리하는 시도를 했었지만 이는 토큰 간의 완전한 spatiotemporal relation을 학습할 수 없습니다.
제안하는 MHRA는 early layer에서 local relation aggregator를 통해 token comparison 연산을 낮추었습니다. 연산을 앞단에서 낮춘 덕분에 뒷단에서는 spatial temporal attention을 분리하지 않고 jointly 하게 attention을 진행했다고 합니다.
Dynamic Position Embedding
이전의 방법들은 absolute 혹은 relative position embedding을 이용했다고 합니다. 여러 가지 position embedding에 대해서는 따로 기회가 될 때 preliminaries에 정리하도록 하겠습니다. 무튼 이러한 position embedding 방식들을 그대로 비디오 데이터에 적용하면 문제가 된다고 합니다.
absolute 방식은 finetuning 과정에서 input size에 따라 embedding을 interpolate 시켜야 하며 relative version은 self-attention weight에 영향을 끼친다고 합니다. 이러한 문제를 해결하기 위해 저자는 dynamic position embedding을 제안합니다.
- DPE(Xin)=DWConv(Xin)
그냥 zero padding을 추가한 3D depthwise convolution입니다. convolution 연산의 shared parameter와 locality에 대한 성질 때문에 DPE는 permutation invariance를 해결할 수 있다고 합니다.
사실 논문 설명이 이게 다라 저는 아직 이해를 못 했습니다.. appendix에도 추가적인 내용은 없어 일단 리뷰에는 내용을 일단 그대로 적는 형태로 마무리하겠습니다.
Experiments
Comparison to state of the art
Kinetics 400 & 600
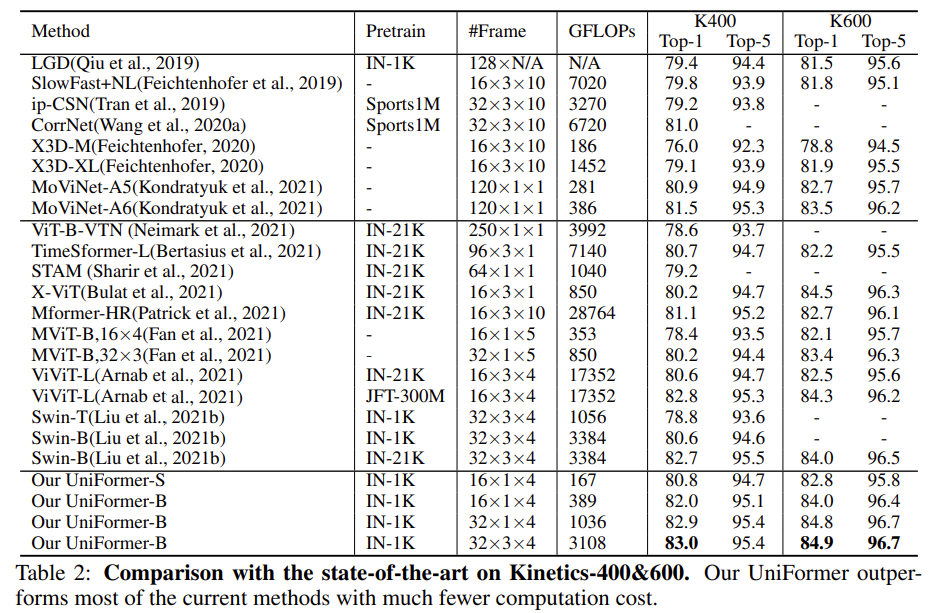
테이블이 위아래로 구분되어 있는데 위의 방법론들은 3D Convolution 계열이고 아래의 방법론들은 Transformer 계열입니다. 위쪽의 SlowFast와 비교하면 Uniformer-S 기준으로 42배 연산량이 적으면서도 1.0% 정확도가 높은 것을 볼 수 있습니다. MoViNet이라는 것과도 비교해 보면 더 적은 입력 프레임을 사용함에도 더 좋은 성능을 보여주고 있습니다.
Transformer 계열과 비교해도 Uniformer는 우수함을 보여줍니다. ImageNet-1K만을 사용해도 제일 좋은 성능들을 보여주고 있습니다. Video Vision Transformer라 불리는 ViViT-L pretain with JFT-300M 과는 성능이 비슷하지만 사전학습 데이터의 양과 GFLOPs 측면에서는 Uniformer가 훨씬 가볍다는 것이 또 다른 장점인 것 같습니다.
Something-Something V1 & V2
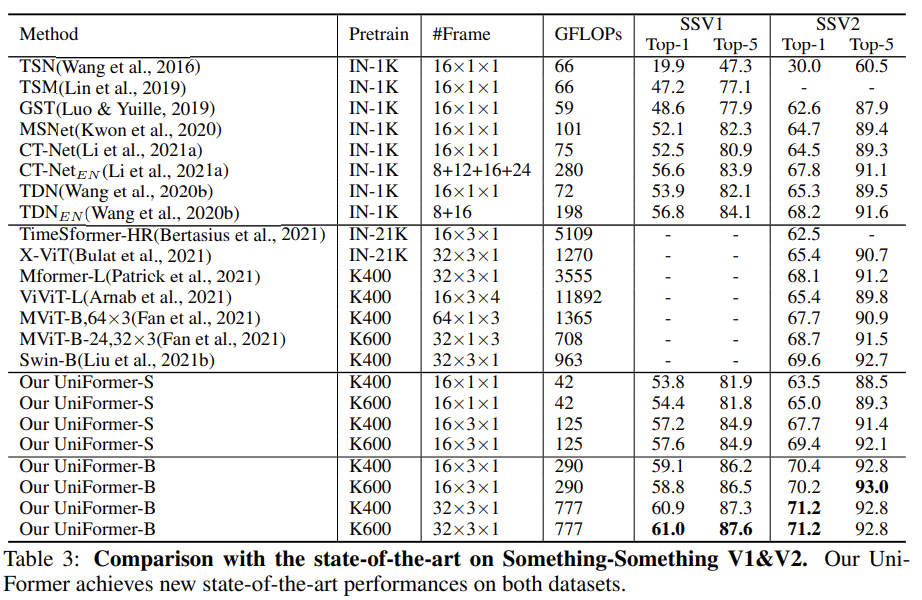
Something-Something 데이터는 temporal relation modeling이 중요한 데이터입니다. 따라서 long-term dependencies를 잘 modeling 하는 Transformer 계열의 방법론들이 더 우수한 성능을 보여줍니다.
Kinetics 데이터 셋과 비슷하게 Uniformer가 좋은 computation-accuracy trade-off를 보여주며 좋은 성능을 나타내고 있습니다. 보통 이 정도로 효율적인 모델이면 사전 학습 하는데 며칠 걸린다 알려주기도 하는데 그런 부분은 없는 게 조금 아쉽네요.
Ablation Studies
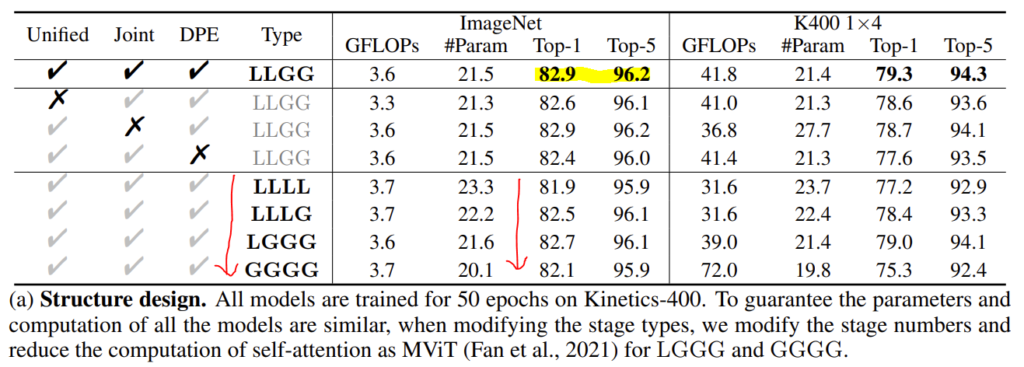
테이블이 4개 정도 나오는데
- Unified라는 의미는 저자가 제안한 local MHRA는 사용한 것이고 이에 대한 X는 MobileNet Block을 사용한 것입니다.
- Joint라는 의미는 spatio-temporal attention을 같이 진행한 것이고 이에 대한 X는 attention을 spatial, temporal 따로 진행한 것입니다.
- L은 Local MHRA를 의미하고 G는 Global MHRA를 의미합니다.
Uniformer vs Convolution : Does transformer style FFN help?
Uniformer의 shallow layer에서 활용되는 Local MHRA가 MobileNet의 PWConv-DWConv-PWConv의 구조를 닮았다고 하지만, transformer style의 MHRA가 더 효과적임을 증명하기 위한 ablation입니다.
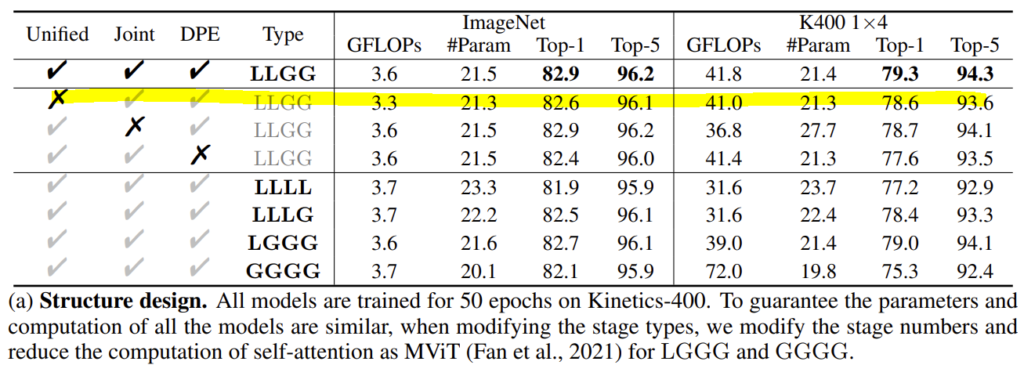
두 번째 행에 해당되는, Unified X에 대응되는 것과 비교하면 비슷하지만 조금 더 우수한 성능을 보여줍니다. 근데 이게 GFLOPs 관점에서는 둘이 거의 차이가 없는 거 같고 성능 면에서도 비슷한 거 같습니다. Backbone 논문을 많이 안 읽어봐서 이게 강조할만한 차이인지는 제가 잘 모르겠습니다.
Uniformer vs Transformer : Is Joint or divided spatiotemporal attention better?
Uniformer의 deep layer에서 활용되는 Global MHRA는 transformer의 self-attention과 동일합니다. 다만 기존의 연구와 다르게 jointly 하게 attention이 진행된다고 하였는데 정말 효과적인지에 대한 ablation입니다.
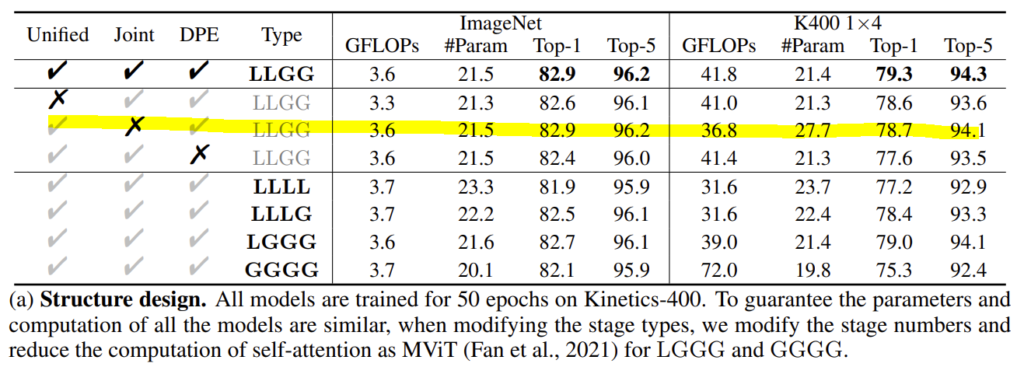
위의 테이블만을 가지고는 저는 사실 강조할만한 차이인지는 모르겠지만 아래의 transfer learning 실험에 대한 결과를 보면 jointly attention 방식이 transfer learning에 좀 더 잘 먹히는 것 같긴 합니다.
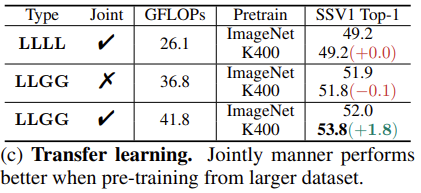
LLGG에서 Jointly 하게 했을 때와 하지 않았을 때를 비교하면 유의미한 성능 차이가 발생하고 있습니다.
Does dynamic position embedding matter to Uniformer?
DWConv으로 정의되어 비교적 간단(?)했던 Dynamic position embedding에 대한 ablation입니다.

사실 Depth-Wise Convolution으로 인해 좀 더 spatio-temporal position을 잘 인코딩할 수 있다는 논리적 설명이 부족한 거 같아 저는 아직도 이해가 잘 가질 않지만 그래도 성능적인 측면에서는 꽤 효과적인 것을 보면 나름의 효과가 있던 모양인 것 같습니다.
How much does local MHRA help?
여기서는 local MHRA와 global MHRA의 비율을 조절하면서 ablation을 진행합니다. Local MHRA만 사용한 LLLL의 경우 Kinetics에서 GFLOPS 측면에서는 이득이 있지만 성능이 꽤나 많이 떨어지는 것을 확인할 수 있습니다. 저자는 이러한 이유가 Long-term dependency를 해결하지 못하기 때문이라 합니다.
LLLL에서 Global을 점진적으로 추가할 경우 성능이 조금씩 좋아지다가 모두 Global MHRA로 대체(GGGG)로 가면 다시 성능이 떨어지고 있습니다. Local redundancy 역시 해결해야 하기에 Local MHRA 역시 중요하다는 의미겠죠. 최종적으로 LLGG가 가장 좋은 성능을 보여주며 local redundancy, global dependency를 효과적으로 해결한 것 같습니다.
Visualization
Attention이 어떻게 되고 있는 지를 보여주기 위해 Grad-CAM 시각화를 진행하였네요.

Global만 사용하는 GGGG의 경우 key object(skate board, foot ball)를 찾는데 어려워하는 모습이 보입니다.
Local만 사용하는 LLLL의 경우 특정 부분에만 활성화가 되어 있어 부정확하네요.
LLGG가 key object와 입력 전반적인 정보를 잘 흡수하는 것 같습니다. 어느 정도 video의 local redundancy 문제와 global dependency 문제를 해결할 수 있을 것 같네요.
Conclusion
video의 local redundancy 문제와 global dependency 문제를 해결하기 위해 3D Convolution의 성질과 Vision Transformer의 성질을 묶어버린 구조를 제안한 논문이었습니다.
논문을 통해 비디오를 이해하는 관점에서 3D Convolution과 Vision Transformer의 차이를 더욱 잘 이해하게 된 것 같습니다.
리뷰 읽어주셔서 감사합니다.



