Before Review
이번 논문은 Video Understanding을 위해 제안되는 temporally adaptive convolution을 다룬 논문입니다. 모든 프레임에 대해서 고정된 weight를 사용하는 기존 Convolution 대비, 입력 값에 따라 weight가 달라지는 dynamic transformation의 성격을 가지는 Convolution이라 볼 수 있습니다.
약간 Self-Attention + Convolution을 섞은 것 같은 느낌이라 볼 수 있을 것 같네요.
제안되는 방법은 Plug and Play 가 굉장히 간단하고 성능이 우수함을 보여주는 것 같아 나중에 제가 어떤 모델을 사용하든 고려할 수 있는 선택지가 될 수 있을 것 같습니다.
리뷰 시작하도록 하겠습니다.
Introduction
Convolution 연산은 현대의 deep vision model 하면 빠질 수 없는 핵심 연산으로 자리 잡아 왔습니다. 이미지 분야에서 많은 발전과 성공을 거둔 Convolution은 자연스럽게 비디오 분야에서 2D->3D의 형태로 발전되어 왔습니다.
3D convolution 형태 그대로 가져가는 연구도 진행되었지만, 효율성 측면에서 3D의 구조를 2D + 1D의 형태로 분할하는 연구도 많이 진행이 되었습니다.
3D를 그대로 가져가면 계산 복잡도가 $O(K^{3})$이 되겠지만 2D + 1D로 분할하면 $O(K^{2}) + O(K)$로 더 적게 가져갈 수 있기 때문이죠.
Spatial 축에 대해서 2D Convolution을 먼저 하고, Temporal 축에 대해서 1D Convolution을 진행하는 형태라 보시면 됩니다.
이렇게 연산을 분할하여 Large-Volume의 비디오 데이터를 처리하려는 연구가 많이 진행되었지만 1D Temporal Convolution은 여전히 무시할 수 없는 computation overhead를 제공한다고 합니다. 따라서 저자는 spatial convolution이 temporal modeling 능력까지 갖추도록 설계하여 1D temporal convolution을 제거하려고 합니다.
일단 Convolution의 하나 중요한 특성은 바로 translation invariance입니다. 이는 Convolution의 local connectivity와 kernel의 shared weight 때문에 발생하는 특성입니다. 하지만 최근 shared weight를 사용하는 것이 아닌 dynamic filtering들은 모든 local pixel에 대해서 shared weight를 사용하는 것은 sub-optimal 하다고 합니다.
저자 역시 temporal convolution을 수행할 때 고정된 shared weight를 사용하는 것보다는 adaptive 한 weight를 사용하는 것이 temporal modeling에 더욱 optimal 하다 주장합니다. 이전의 dynamic filtering 기반의 방법들을 가지고 adaptive 한 filtering을 수행할 수 있지만 두 가지 문제점이 존재한다고 주장합니다.
- Dynamic filtering을 하면 기존 pretrain 모델을 사용할 수 없습니다.
- 기존의 Dynamic filtering은 temporal context가 아닌 spatial context를 가지고 생성되기 때문에 temporal modeling에 적합하지 않습니다.
저자는 이제 프레임들끼리 공유하는 weight가 아닌 adaptive한 weight를 temporal 축에 대해서 진행할 수 있는 Temporally-Adaptive Convolution(TAdaConv)를 제안합니다. Adaptive 한 weight를 만들어내는 대표적인 연산이 Self-Attention입니다. 따라서 본 논문은 Convolution의 연산을 그대로 가져가지만 여기에 temporal 차원에 대한 Self-Attention이 진행되었다고 볼 수 있겠네요.
저자가 주장하는 TAdaConv의 핵심은 weight calibration 입니다. 구체적으로 $t$ 번째 프레임의 kernel weight를 $W_{t}$라고 하겠습니다. 그리고 이 $W_{t}$를 $W_{t}=a_{t} \cdot W_{b}$ 이렇게 분할시킵니다.
- $a_{t}$ : calibration weight로 frame 마다 서로 다른 weight 값을 가집니다. 이 calibration weight는 인접한 프레임들끼리의 relation 정보를 활용하여 생성되며 이를 토대로 temporal modeling을 진행하게 됩니다.
- $W_{b}$ : base weight로 사전 학습된 weight를 사용합니다.
$W_{t}$를 $W_{t}=a_{t} \cdot W_{b}$ 이렇게 modeling 하는 이유에 대해서는 뒤에서 좀 더 자세히 다루도록 하겠습니다.
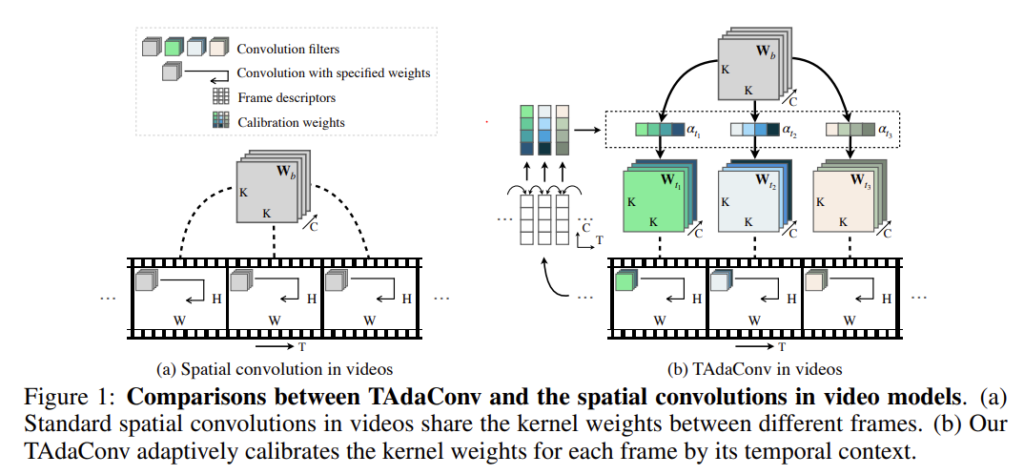
제안하는 TAdaConv와 spatial convolution 간의 차이는 위의 그림을 통해 확인할 수 있습니다. 본 논문에서 제안하는 TAdaConv는 아래와 같은 장점을 가집니다.
- TAdaConv는 기존 모델의 pre-trained weight를 여전히 사용하면서 쉽게 plug and play 방식으로 spatial convolution을 대체할 수 있습니다. 이를 통해 temporal modeling 능력을 강화시키는 것이죠.
- 학습된 2D feature map에 temporal 1D convolution을 하는 것보다 TAdaConv는 더욱 효율적으로 동작합니다.
연산 복잡도가 어떻게 차이 나는 지는 바로 뒤에서 다루도록 하고 이제 본격적으로 제안되는 연산이 어떻게 정의되는지 살펴보도록 하겠습니다.
TADAConv : Temporally-Adaptive Convolutions
Revisiting temporal convolutions
일단 temporal convolution을 다시 한번 revist 하여 calibration weight라는 insight가 어떻게 도출되었는지 살펴보도록 하겠습니다. Simplicity를 위해 depth-wise temporal convolution을 진행하였고, $ 3 \times 1 \times 1 $의 크기를 가지고 $\beta = [\beta_{1},\beta_{2},\beta_{3}]$과 같이 변수화 되는 filter를 고려하였습니다.
$W$라는 weight를 가지는 2D convolution을 통과한 output $\tilde{x}_{t}$ 은 아래와 같이 정의됩니다.

$\delta$는 ReLU activation입니다. Temporal weight에 따른 linear combination 형태입니다. 그리고 이를 다시 정리하면 아래와 같습니다.
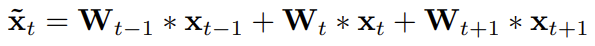
각각 입력이 어떻게 들어오는지에 따라 activation의 결과가 달라지기 때문에 frame 마다 다른 결과를 만들어냅니다. 즉, $W_{t-1}$, $W_{t}$ 그리고 $W_{t+1}$는 모두 다른 값을 가지게 됩니다. 이를 좀 더 일반적인 형태로 formulation 하면 아래와 같습니다.
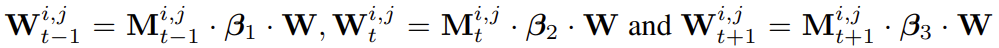
$M_{t} \in \textbf{R}^{C\times H\times W}$는 dynamic tensor입니다. Spatial convolution 결과에 따라 값이 변경되는 tensor라는 것입니다. 2D spatial convolution이 진행되고 1D temporal convolution의 과정입니다.
그런데 사실 $W$라는 base weight와 인접 프레임간의 연산을 통해 temporal modeling을 잘 수행할 수 있는 dynamic tensor를 얻을 수 있다면 1D temporal convolution은 수행할 필요가 없습니다.
Formulation of TAdaConv
앞서 temporal convolution을 revisit 하는 과정에서 결국 $t$ 번째 convolution은 결국 base weight와 calibration weight의 곱으로 표현할 수 있다고 했습니다. 아래와 같이 말이죠.
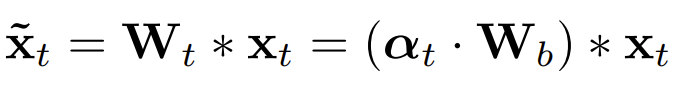
$W_{b}$는 사전 학습된 2D spatial convolution weight를 사용하면 되기 때문에 핵심은 calibration weight은 $a_{t}$를 잘 계산하는 것이죠. 논문의 목적답게 temporal modeling 능력을 갖추도록 말입니다.
Calibration weight generation
Temporal dynamics를 modeling 하기 위해서는 temporal context를 고려하는 calibration weight $a_{t}=$ 잘 만드는 것이 중요합니다. Weight generation의 전체적인 과정은 아래 그림과 같습니다.
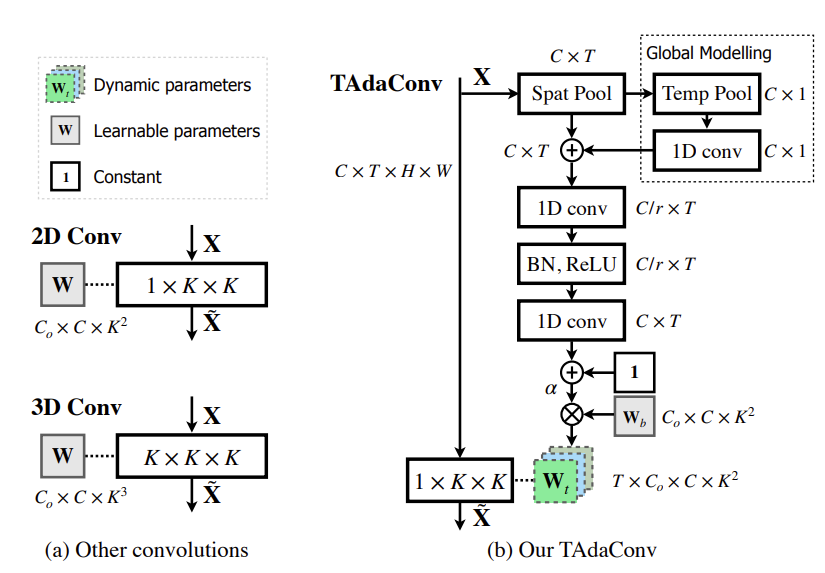
기존의 Convolution 연산은 (a) Other convolutions를 확인하면 알 수 있고 constant weight로 연산이 수행되고 있습니다.
TAdaConv는 1D temporal convolution으로 발생하는 computation overhead를 줄이는 것이 일차적인 목적이기 때문에 efficiency를 고려해야 합니다. 따라서 저자도 효율성을 위해 frame description vector를 생성하는 과정을 굉장히 간단하게 진행했습니다. 그냥 spatial 축에 따라서 average pooling을 때려버립니다.
즉, $x_{t} \in \mathbb{R}^{C\times H\times W\times T}$의 frame tensor의 $H\times W$ 축에 대해서 평균 연산을 취해 $v_{t} \in \mathbb{R}^{C\times T}$의 형태로 만들겠다는 의미입니다.
- $v_{t}=GAP_{s}(x_{t})$ : 간단하지만 여기서는 프레임하나를 설명하는 descriptor가 되는 것입니다.
그래서 이렇게 인접한 context 내에서 $v_{t}$를 모아 $v_{t}^{adj}=[v_{t-1}, v_{t}, v_{t+1}]$와 같은 local context를 만듭니다. 이렇게 local context 정보가 있어야 temporal modeling 이 가능한 weight를 생성할 수 있겠죠.
그리고 stacked two-layer 1D convolution을 통과시킵니다. 의아할 수 있는 것은 1D temporal convolution의 연산량을 없애려고 지금 새로운 연산을 구상 중인데 갑자기 1D convolution을 두 번이나 하겠다는 것이 이해가 안 될 수 있습니다.
저자는 이러한 의문을 없애기 위해 단순히 1D convolution을 하는 것이 아니라 채널축에 대해서 차원을 감소시켰다 다시 늘리는 방향으로 연산량을 줄였다고 합니다.
예를 들어 채널이 100->100으로 나오는 것이 나면 필요한 연산은 $100\times 100$ 입니다. 하지만 100->10, 10->100 이렇게 하면 필요한 연산은 $100\times 10 + 10\times 100 = 2000$ 이렇게 되겠죠?
그래서 $\gamma$라는 dimension reduction factor를 정의하여 연산량을 조절합니다.

여기서 BN은 batchnorm 이고$\delta$는 ReLU activation입니다.
저자는 여기에 global 정보를 추가하기 위해 global descriptor를 정의합니다. Global descriptor라고 해서 대단한 건 아니고 temporal 축에 대해서도 이제 평균 때리는 겁니다. Sptial-temporal 축에 대해서 모두 평균 내고 FC layer를 한번 태워준 것을 global descriptor라고 정의하고 있습니다.
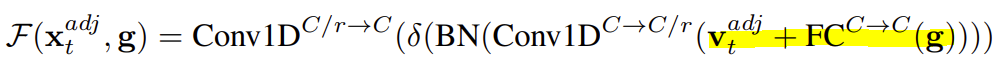
무튼 이렇게 정의된 연산은 결국 local context와 global context를 토대로 convolution 연산을 통해 무언가 output을 만들어냅니다. 이 output이 결국 calibration weight를 책임지는 dynamic tensor가 될 것이라 기대하는 것이죠.
Initialization
제안되는 TAdaConv는 기존 2D spatial convolution을 대체할 수 있습니다. 따라서 초기화 방법도 2D spatial convolution과 동일하게 가져갔다고 하네요. 마지막 convolution의 weight를 zero-initializing을 하고 1로 구성된 constant vector를 더하는 것으로 초기화를 한다고 합니다.
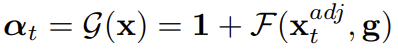
Initial state에서는 $W_{t}=1,W_{b}=W_{b}$로 세팅하고 $W_{b}$는 pretrain weight입니다.
Calibration dimension
위의 설명 흐름을 잘 따라오고 직접 한번 계산해 보면 calibration weight의 차원을 계산할 수 있습니다.
- $a_{t} \in \mathbb{R}^{1\times C_{in}\times 1}$ : 들어오는 채널의 크기만큼 adaptive 한 weight가 생성됩니다.
Base weight의 차원이 $W_{b} \in \mathbb{R}^{C_{out}\times C_{in}\times k^{2}}$입니다. 기존의 spatial convolution 역시 서로 다른 채널에 대해서 다른 weight를 가지고 있지만 temporal modeling 능력까지 갖추고 있지는 않았습니다.
TAdaConv에서는 calibration weight를 가지고 다시 weight를 부여하기 때문에 temporal modeling의 능력을 갖추기를 기대할 수 있겠죠.
Comparison with other dynamic filters
앞서 introduction 부분에 기존 dynamic filter들의 한계점에 대해서 얘기했습니다. 아래 테이블을 보시면 세 가지 항목에 대해서 기존의 work들을 정리하였네요.

Temporal modeling이나 Pretrained weights는 직관적인 것 같아 Location adaptive만 설명해 보자면 서로 다른 위치에 대해서 adaptive 한 weight가 생성되는지를 묻는 항목입니다.
저는 여기서 의문이 하나 들었습니다. 일단 Location adaptive나 Pretrained weights는 당연하게 고려되고 있습니다. 구조 자체가 그렇게 설계되었기 때문입니다.
하지만 Temporal modeling은 확실한 것이 아니라 기대하는 수준이지 않나?라는 의문이 들었습니다.
사실 local, global descriptor를 만드는 과정도 너무 간단해서 표현이 구별력을 가지는지에 대해서도 의문이 들고 temporal convolution 두 번 때리는 게 왜 temporal modeling이 강화되는지 그 논리의 흐름을 잘 이해하지 못했습니다.
그래도 실험 부분에서 무언가를 보여주길 기대하면서 일단 이 정도로 마치겠습니다.
Comparison with temporal convolutions
저자가 분명히 2D + 1D convolution의 형태가 무시할 수 없는 computation overhead를 초래하기 때문에 더 효율적인 연산구조를 제안하겠다고 했습니다. 따라서 FLOPs를 비교해 보도록 하겠습니다.

사실 FLOPs 부분에서 2D convolution에 해당되는 complexity는 동일합니다. 비교는 1D Convolution과 TAdaConv의 calibration weight를 만드는 부분이겠네요. 저는 일단 제가 직접 계산을 해보지 않았습니다. 궁금하시면 appendix에 있는 것 같으니 찾아보시고 결과만 놓고 비교해 보도록 하겠습니다.
빨간색이나 초록색으로 칠해진 숫자는 단순히 2D Convolution과 비교했을 때 발생하는 추가적인 FLOPs/Params입니다.
TAdaConv는 확실히 기존 2D + 1D convolution에 비해 연산량을 적게 가져가는 것 같습니다. 효율성 측면에서는 더 좋다는 것을 확인했으니 이제 정량적으로 video classification과 action localization에서도 좋은 성능을 보여주는지 확인해 보도록 하겠습니다.
TADA2 D : Temporally-Adaptive 2D Networks
저자는 TAda Convolution이 2D spatial convolution 대체할 수 있으니 기존 2D Convolution을 사용하는 대표적인 network의 일부 convolution 연산을 제안되는 TAda Convolution으로 대체하는 network를 제안합니다.
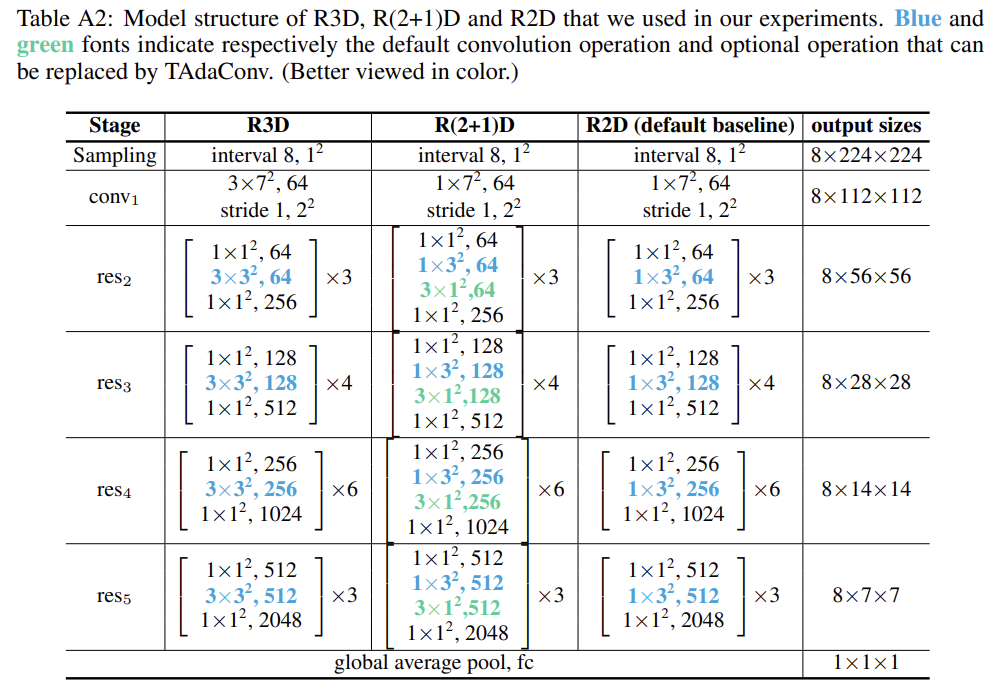
파란색 커널은 TAdaConv로 대체하는 부분이고 초록색 커널들은 옵션이라고 하네요.
다음으로 이 제안되는 새로운 2D network 같은 경우들은 TAdaConv를 한 다음 temporal feature aggregation을 진행한다고 합니다. 그 이유에 대해서는 자세히 나와있지 않지만 feature 가지는 temporal 차원에 대해서 average pooling을 하고 그 정보를 다시 더해주는 것을 보니 shortcut connection 느낌으로 하고 있네요.
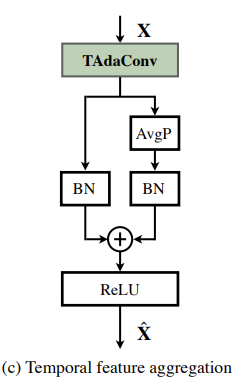
특이한 게 여기 나와있는 두 개의 BatchNorm의 weight 초기화를 다르게 한다고 합니다. 왼쪽의 BatchNorm은 pretrain weight이며 오른쪽의 BatchNorm은 zero로 초기화를 하네요.
Experiments on Video Classification
TAdaConv on Existing Video Backbones
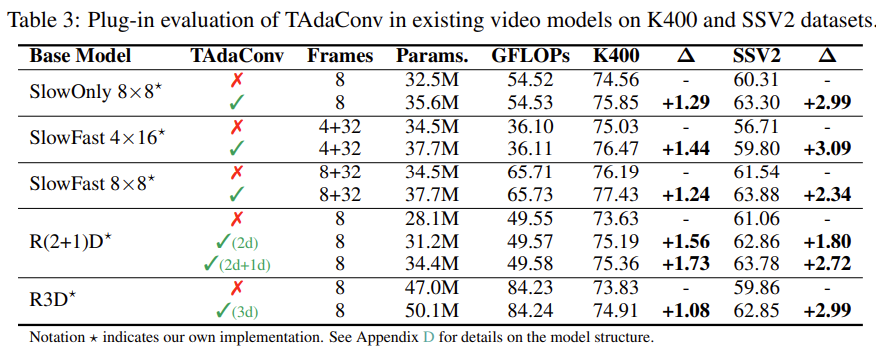
Video Classification에서의 성능 평가입니다. TAdaConv는 모델이 아니라 연산이기 때문에 다른 Backbone에 추가하고 plug-and-play 방식으로 성능을 평가하였습니다.
TAdaConv를 추가하면 Params의 증가는 조금 발생하지만 GFLOPs의 변화는 크지 않은 것을 확인할 수 있습니다. Kinetics 그리고 SSV2와 같은 대표적인 Classification Benchmark 데이터 셋에서 좋은 성능을 보여주는 것이 인상 깊습니다.
Ablation Studies
Dynamics vs learnable calibration
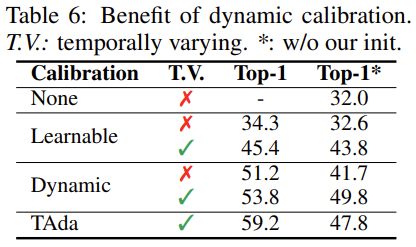
None은 이제 베이스라인이라 잡으면 됩니다.
Learnable은 calibration weight를 단순히 learnable 하게 만들어 놓은 것입니다.
Dynamic은 global descriptor에 의해서만 dynamic 하게 calibration weight를 만들어 놓은 것입니다.
Learnable의 경우 단순히 학습 가능한 Layer만 태운다고 해서 temporal modeling 능력이 생기는 것은 아니기 때문에 성능이 제한되는 것 같고, Dynamic의 경우는 local context까지는 고려하지 못했기 때문에 부족한 모습을 보이는 것 같습니다.
추가적으로 테이블을 보시면 *로 구분이 되어 있는데 이는 저자들이 제안하는 초기화 방법을 사용했을 때와 하지 않았을 때의 차이를 나타내고 있습니다. TAdaConv의 경우 초기화 방법에 따라 성능이 드라마틱하게 차이가 나네요.
여담이지만, 이런 결과를 놓고 봤을 때 어쩌면 우리가 실험을 할 때 아이디어와 설계 자체는 타당한데 실험이 이상하게 결과가 안 나오는 경우가 있었을 겁니다. 그랬을 때 이런 사소한 디테일이 중요하게 작용할 수 있다는 것을 깨닫게 해 주네요.
Calibration weight generation function

Calibration weight generation 과정에서 어떤 함수들을 사용하는지에 따른 ablation입니다.
Lin은 activation 없이 하나의 Linear Layer만을 사용하는 경우입니다.
Non-Lin은 Linear-batchnorm-activation-Linear 이렇게 사용하는 경우입니다.
K는 kernel size로 1에 가까울수록 local context가 고려되지 않는 것이고 커질수록 그 영역이 넓어진다고 보시면 됩니다.
최종적으로 generation function은 어느 정도 비선형성을 가지면서 kernel은 3 by 3 그리고 global descriptor까지 포함했을 때 성능이 가장 좋은 것을 보여주고 있습니다.
Calibration dimension
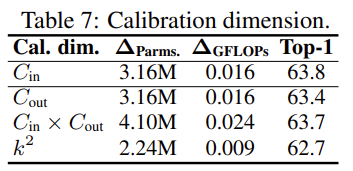
Calibration weight를 생성할 때 사실 그 차원은 여러 가지로 setting 할 수 있습니다. Convolution의 입력 출력 차원을 조정하면 가능하기 때문이죠.
결국 Calibration weight의 차원이 달라진다는 것은 Base Weight에서 어느 차원 축으로 attention이 제공되는지가 달라지는 것과 동일하죠. 결과적으로는 입력 채널수에 맞춰 dimension을 조정하는 게 가장 좋았는데 이는 결국 adaptive 한 weight가 입력에 따라 결정되기 때문에 입력 채널수에 맞추는 게 가장 좋지 않나 이렇게 주장하고 있습니다.
Visualizations

시각화 결과입니다. Main paper에는 이 정도만 보여주고 있습니다. 정성적 결과만 놓고 보면 타 방법론 대비 더욱 key point에 잘 집중하는 모습입니다. 다만 예시가 많지 않아 신빙성을 조금 떨어지는 느낌입니다.
Main Results
이제 Video Classification과 Action Localization에 대한 benchmark입니다. SSV2, Epic-Kitchens-100, Kinetics-400 그리고 HACS 데이터셋에 대해서 진행했네요. 맘에 드는 건 SSV2, Epic-Kitchens-100, HACS 등 꽤나 어려운 데이터셋을 가지고 benchmarking을 했다는 것입니다.
다른 논문들을 보면 비교적 쉽고 비디오의 길이가 짧은 UCF나 HMDB로 하는 경우도 많은데 SSV2나 HACS는 비디오 길이도 길고 꽤 복잡하기 때문에 본 방법론이 정말 실제 시나리오에도 적합한지 그 경향성을 확인하는데 더 도움이 될 것 같습니다.
아래 실험에서 TAda2D는 ResNet의 일부 Convolution Layer를 TAdaConv로 대체한 것이고 TAdaConvNext는 ConvNext를 동일하게 변형시킨 것입니다.
SSV2

ConvNext에 TAdaConv를 적용할 경우 가장 좋은 efficiency와 accuracy trade-off 관계를 보여주고 있습니다.
Epic-Kitchens-100
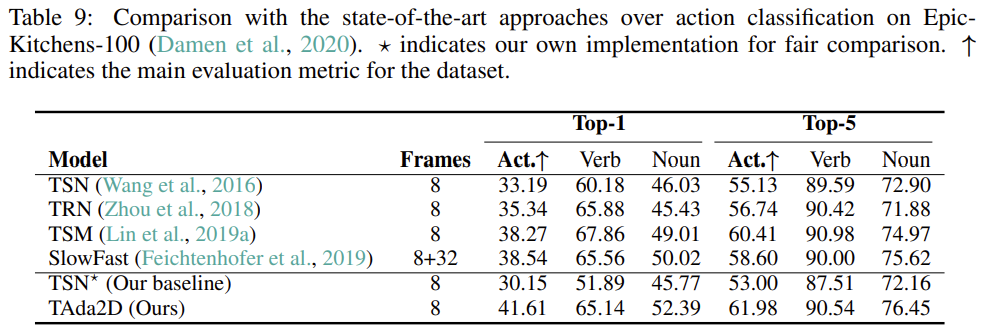
Epic-Kitchens에서는 SlowFast라고 해서 Kaiming He 선생님이 비디오 계의 굉장히 신선한 Backbone을 제안한 연구가 있는데 그것보다 입력 frame은 더 적게 가져가면서 더 좋은 성능을 보여주는 것이 인상 깊습니다.
Kinetics-400
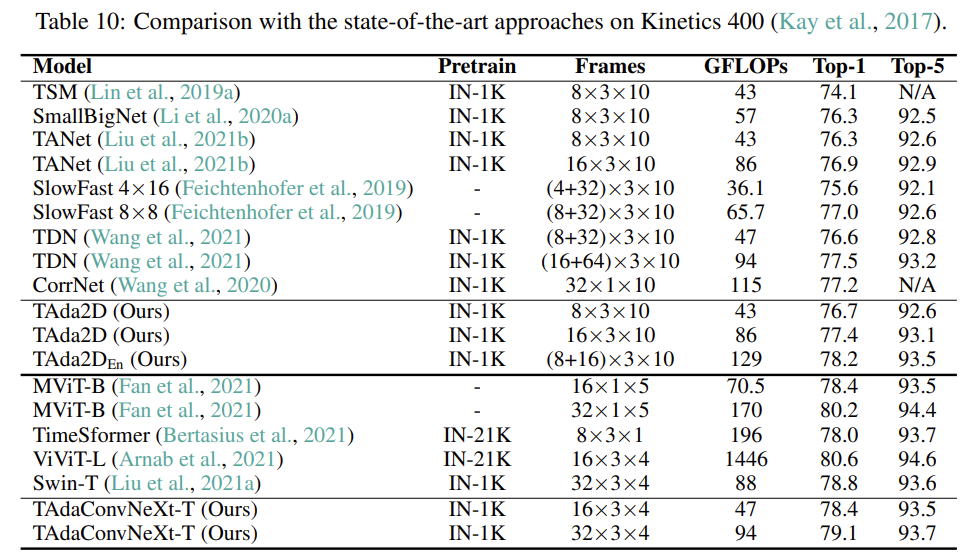
Kinetics에서는 성능이 무조건 SOTA는 아닌데 GFLOPs 대비 굉장히 좋은 성능을 보여주기 때문에 contribution은 충분한 것 같습니다.
Experiments on Temporal Action Localization
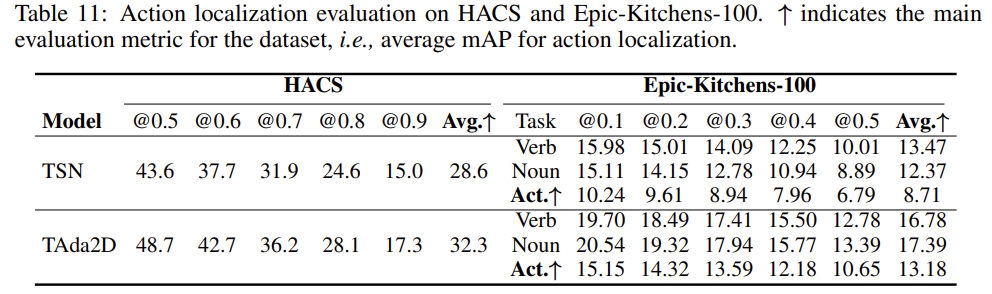
Action Localization에서도 TAdaConv가 좋은 모습을 보여주고 있습니다. Classification 뿐만 아니라 Localization에서도 좋은 성능을 보여주며 task에 국한되지 않고 좋은 generality를 가진다는 것을 보여주고 있습니다.
결국 Pretrained Weight를 사용할 수 있다는 장점 덕분에 잘만 사용하면 Localization SOTA method들의 성능을 더욱 높일 수 있을 것 같습니다.
제가 방법론을 설명하면서 TAdaConv가 왜 temporal modeling 능력을 가지게 되는지에 대해서는 조금 의문을 품었는데 실험 결과를 보면 temporal modeling 능력이 중요한 Localization task에서도 좋은 경향성을 보여주기 때문에 이러한 의문에 대해서는 어느 정도 해소가 된 것 같습니다.
Conclusion
제안되는 방법은 Plug and Play 가 굉장히 간단하고 성능이 우수함을 보여주는 것 같아 나중에 제가 어떤 모델을 사용하든 고려할 수 있는 선택지가 될 수 있을 것 같습니다.
잘 기억하고 있다가 필요할 때 적재적소에 사용하도록 하겠습니다.
리뷰 읽어주셔서 감사합니다.



