Intro
지난 글에서는 convex function의 정의와 몇 가지 예제들 그리고 그 예제들이 정말로 convex function인지 같이 증명을 해보았습니다.
Optimization Theory (Convex Functions Ⅰ)
Intro지난 포스팅에서는 convex set의 정의를 살펴봤습니다. 이번 포스팅에서도 비슷하게 convex function의 정의를 알아보고, 다양한 예시 그리고 함수의 convexity를 보존하는 연산들을 살펴볼 것입니다.
taek-guen.tistory.com
이번 글에서도 convex function과 관련된 내용을 알아 볼 것인데, convex function의 convexity를 보존하는 연산들을 살펴보고 quasiconvex function에 대해서 알아보고 마치도록 하겠습니다.
Convex Functions
5. Operations that preserve convexity
이전 포스팅에서 convex set의 convexity를 유지할 수 있는 연산들을 살펴봤습니다. 이번에는 convex function의 convexity를 유지하게 하는 연산들에 대해서 알아보겠습니다.
우리가 잘 알고 있는 convex function을 이용하여 새로운 convex function을 도출할 수 있습니다. 결국 최적화 문제에서 목적 함수를 변환하거나 이해하는 관점에서 이런 연산들을 잘 숙지하는 것이 중요하기 때문이죠.
어려운 내용은 아니기 때문에 같이 한번 알아보도록 하겠습니다.
Nonnegative weighted sums
우선, 임의의 convex function $f$ 가 있다고 가정해보겠습니다.
1. 양의 실수 $\alpha$에 대해서 $\alpha \cdot f$ 역시 convex function이라는 것을 알 수 있습니다.
양의 실수곱은 스케일의 변화만 가져오고 convex function의 정의에 해당하는 부등식을 그대로 유지시키기 때문입니다.
2. $f_{1}+f_{2}$역시 convex function이라는 것 역시 직관적으로 알 수 있습니다.
그래서 양의 실수배와 덧셈을 결합하면 convex function으로 만들어내는 새로운 convex function을 정의할 수 있습니다. 책에서는 convex cone이라고 표현을 하네요.
- $f=w_{1}f_{1}+\ldots +w_{n}f_{n}$
유사하게 concave function 끼리의 nonnegative weighted sum은 concave function입니다.
Composition with an affine mapping
다음으로는 affine mapping입니다. 우리가 convex set에 affine transform을 가해도 convexity가 보존된다는 것은 이전 글에서 살펴본 적이 있습니다. 따라서 정의역에 affine transform을 가해도 정의역은 여전히 convex set이기 때문에 convex function이라는 것이 보존이 됩니다.
- $g(x)=f(Ax+b)$
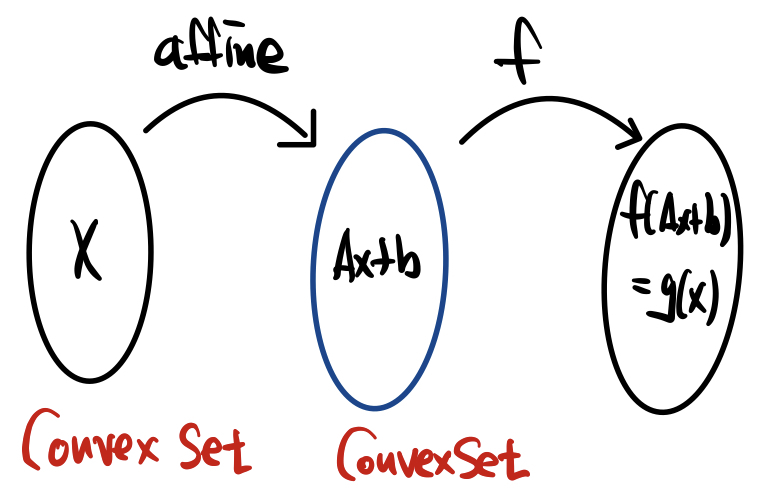
결국 $f$가 convex function이라면 $g(x)=f(Ax+b)$ 역시 convex function이라는 것입니다.
Pointwise maximum and supremum
Convex function 끼리의 pointwise-maximum 연산 역시 convexity를 보존합니다. 그림으로 먼저 본다면 직관적으로 이해할 수 있어 확인하겠습니다.
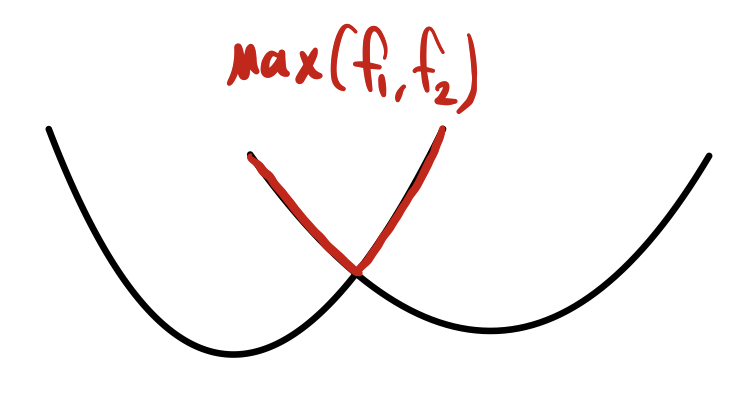
빨간색으로 칠해진 부분이 두 function 간 max value를 나타내는 것인데, convex 한 형태를 보여주고 있습니다.
- $f(x)=\max\left\{ f_{1}(x),f_{2}(x)\right\},\, \text{where} \,\text{dom}(f)= \text{dom}(f_{1}) \bigcap \text{dom}(f_{2})$
Max function 자체가 convex function이기 때문에 증명의 과정은 간단합니다. 이와 비슷하게 concave function의 pointwise minimum은 역시 concave function입니다.
Composition
합성 함수를 이용하여 convex function을 만들 수 있습니다. 모든 case에서 성립하는 것은 아니고, 몇 가지 조건이 충족될 때 convex 혹은 concave function을 새롭게 정의할 수 있습니다.
$g:\mathbb{R}^{n}\rightarrow \mathbb{R},h:\mathbb{R}\rightarrow \mathbb{R}$가 있다고 가정하겠습니다.
n=1에 해당하는 scalar composition 상황을 먼저 보도록 하겠습니다.
$f(x)=h(g(x))\rightarrow f^{\prime \prime }(x)=h^{\prime \prime }(g(x))g^{\prime }(x)^{2}+h^{\prime }(g(x))g^{\prime \prime }(x)$
- $f^{\prime \prime }(x) \geq 0$ 가 보장된다면 convex function일 것이고,
- $f^{\prime \prime }(x) \leq 0$ 가 보장된다면 concave function 일 것입니다.
하나 예를 들어보겠습니다.
만약 $h$가 convex function이고, nondecreasing 함과 동시에 $g$가 convex 하다면 $f$는 convex입니다.
$h$와 $g$ 가 convex 하다면 $g^{\prime \prime }(x),h^{\prime \prime }(x)$는 항상 양의 값을 가지게 됩니다.
이 상황에서 $h$가 감소하지 않은 함수이기 때문에 $h^{\prime }(x)$역시 항상 양의 값을 가지게 됩니다.
수식에 하나씩 대입하면 $f^{\prime \prime }(x)$가 양수라는 것이 보장되네요.
다음으로는 $n>1$에 해당하는 vector composition을 살펴보겠습니다.
$f^{\prime \prime }(x)=g^{\prime }(x)^{T}\nabla^{2} h(g(x))g^{\prime }(x)+\nabla h(g(x))^{T}g^{\prime \prime }(x)$
여기서 중요한 점은 만약 $h(x)$가 convex 하다면, hessian matrix는 positive semidefinite 이므로 $g^{\prime }(x)^{T}\nabla^{2} h(g(x))g^{\prime }(x)$은 항상 양의 값을 가지게 됩니다.
반대로 concave 하다면 음의 값을 가지게 되겠네요.
몇 가지 예시를 통해 살펴보겠습니다.
1. If g is convex, then $h(g(x))=e^{g(x)}$ is convex
여기서 $g(x)$는 convex 하고 $e^{x}$는 convex 하면서 non-decreasing function이기 때문에
$h(g(x))$ 역시 convex function입니다.
2. If g is concave and positive, then $1/g(x)$ is convex
$h(x)=\frac{1}{x} $는 convex 하면서 non-increasing function입니다.
따라서 $0\leq h^{\prime \prime }(x),h^{\prime }(x)\leq 0$이 성립합니다.
$g(x)$는 concave function이기 때문에 $g^{\prime \prime }(x)\leq 0$ 입니다.
그대로 저기 보이는 판별식에 넣어주면 convex function이라는 것이 보장이 됩니다.
Minimization
위에서 임의의 convex function의 집합의 maximum 혹은 supremum function 역시 convex 하다는 것을 우리는 알아봤습니다. 비슷하게 $f$가 $(x,y)$에서 convex 하다고 할 때, 아래의 함수 역시 convex 합니다.
$g(x)=\inf_{y\in C} f(x,y)$
근데 여기서 $g(x)$가 의미하는 것은 무엇일까요?
저도 이 부분을 해석하는 것이 조금 어려웠습니다.
$f(x,y)$가 있을 때 $y\in C$에 해당하는 특정한 $\hat{y} $이 있다고 가정하겠습니다.
y가 특정한 상수로 고정이 되었으니 $\inf_{y\in C} f(x,y)$는 $x$에 대한 함수입니다.
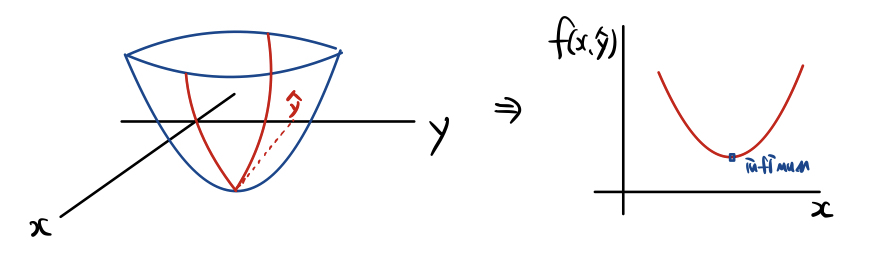
$\text{dom}(g)=\{ x|\left( x,y\right) \in \text{dom}(f),y\in C\} $
그래서 $g(x)$의 정의역은 $f(x,y)$의 정의역을 $x$축으로 투영시킨 것이라 보면 됩니다. 직관적으로는 받아들이기 조금 버거운 감이 있습니다. 고로 증명을 한번 해보도록 하겠습니다. 증명을 하기에 앞서 몇 가지 가정들을 하고 가겠습니다.
임의의 $y_{1},y_{2}\in C$에 대해 $f(x_{i},y_{i})\leq g(x_{i})+\epsilon,\; \text{for}\, i=1,2.$이 성립한다고 가정하겠습니다.
$g(x_{i})$는 하한이지만, 거기에 $\epsilon$을 더했다는 것은 $y_{1},y_{2}\in C$가 하한에 굉장히 근접한 point라는 것입니다. 하한에 굉장히 근접한 극한점이라고 생각하면 되겠습니다.
Convex function의 정의를 정리해보면 아래와 같고, 이를 적용하여 증명해 보겠습니다.
- $g(\theta x_{1}+(1-\theta )x_{2})\leq \theta g(x_{1})+(1-\theta )g(x_{2}), \; \theta \in [0,1] $
이 때, $g(x)=\inf_{y\in C} f(x,y)$ 가 convex function의 정의를 만족시킬 수 있어야 합니다.
- $g(\theta x_{1}+(1-\theta)x_{2})=\inf_{y\in C} f\left( \theta x_{1}+(1-\theta)x_{2},y\right)$
그리고 $\inf_{y\in C} f\left( \theta x_{1}+(1-\theta)x_{2},y\right)$는 최소값을 가지기 때문에 아래의 부등식이 성립합니다.
- $\inf_{y\in C} f\left( \theta x_{1}+(1-\theta )x_{2},y\right) \leq f(\theta x_{1}+(1-\theta )x_{2},\theta y_{1}+(1-\theta )y_{2})$
여기서 $f$는 convex 하다는 전제가 있기 때문에 convex function의 정의를 이용한 부등식을 유도할 수 있습니다.
- $f(\theta x_{1}+(1-\theta )x_{2},\theta y_{1}+(1-\theta )y_{2})\leq \theta f(x_{1},y_{1})+\left( 1-\theta \right) f(x_{2},y_{2})$
이때 하한에 굉장히 근접한 $y_{1},y_{2}\in C$ 두 포인트가 있기 때문에 아래의 부등식을 세울 수 있습니다.
- $\theta f(x_{1},y_{1})+\left( 1-\theta \right) f(x_{2},y_{2})\leq \theta g(x_{1})+(1-\theta )g(x_{2})+\epsilon $
이때 $\epsilon$ 은 굉장히 작은 값이고 $\epsilon > 0$에 대해서 항상 성립하기 때문에
- $g(\theta x_{1}+(1-\theta )x_{2})\leq \theta g(x_{1})+(1-\theta )g(x_{2})$
Convex function의 정의를 만족한다는 것을 알 수 있습니다.
Perspective of a function
마지막으로 투영 함수도 convexity를 보존시킵니다. $f(x,y)=x^{2}+y^{2}$ 를 $x$축에 투영시키면 $f(x)=x^{2}$가 되는 것을 생각해보면 됩니다. 우선 Persepctive function의 정의부터 알아보도록 하겠습니다.
- $g(x,t)=tf(x/t)$ , $\text{dom}(g)=\left\{ \left(x,t\right) \,|\, x/t \in \text{dom}(f), t>0\right\} $
입력의 마지막 차원을 1로 정규화시켜서 제거하는 식으로 projection이 진행됩니다. Convex set에서도 알아봤지만 perspective 연산은 convexity를 보존하게 됩니다. 여기서도 동일하게 적용이 됩니다.
- 함수 $f$가 convex function이라면, $f$의 perspective function 역시 convex 합니다.
- 함수 $f$가 concave function이라면, $f$의 perspective function 역시 concave 합니다.
보존이 된다는 것은 직관적으로 받아들일 수 있지만, 이번에는 증명을 한번 같이 해보도록 하겠습니다.
증명은 epigraph를 이용해서 쉽게 할 수 있습니다.
일단 epigraph가 무엇인지 까먹었을 수 있으니 다시 한번 정리하겠습니다. Epigraph는 함수의 위쪽입니다.
- $\text{epi}(f)=\left\{\left(x,t\right) \,|\,x \in \text{dom}(f), f(x) \leq t\right\}$
근데 epigraph는 아주 중요한 성질을 가지고 있습니다.
"어떤 임의의 함수 $f$의 epigraph가 convex function이라는 것은 임의의 함수 $f$가 convex function이기 위한 필요충분조건이다"라는 것입니다.
함수 $g(x,t)=tf(x/t)$의 epigraph가 convex 하다는 것을 밝히면, $g$ 역시 convex function이라는 것을 알 수 있습니다.
- $(x,t,s)\in \text{epi}(g) \Leftrightarrow tf(x/t)\leq s$
- $(x,t,s)\in \text{epi}(g) \Leftrightarrow f(x/t)\leq s/t$
$t$로 나눠주는 것은 투영을 시키는 것이라 보면 됩니다.
- $(x,t,s)\in \text{epi}(g) \Leftrightarrow \left(x/t,s/t\right) \in \text{epi}(f)$
즉, $\text{epi}(g)$는 $\text{epi}(f)$ perspective function에 대해서 inverse image입니다.
함수 $f$가 convex function이므로 $\text{epi}(f)$역시 convex 합니다.
이때 $\text{epi}(g)$는 $\text{epi}(f)$ perspective function에 대해서 inverse image 이므로 $\text{epi}(g)$ 역시 convex 합니다.
$\text{epi}(g)$가 convex 하기 위해서는 함수 $g(x,t)=tf(x/t)$ 역시 convex 하다는 의미입니다.
따라서 증명이 완료되었습니다.
6. Quasiconvex functions
Quasiconvex functions
다음으로는 준볼록 함수(Quasiconvex function)입니다.
이전까지 알아봤던 convex function 보다 더 general 한 function의 정의라고 생각하면 됩니다.
정의는 아래와 같습니다.
임의의 함수 $f:\mathbb{R}^{n}\rightarrow \mathbb{R}$가 있고 $f$의 domain과 sublevel-set이 모두 convex 하다면, 우리는 함수 $f$를 quasiconvex function이라고 정의합니다.
모든 convex function은 quasiconvex function입니다.
그럼 일단 quasiconvex function의 그래프를 한번 보도록 하겠습니다.
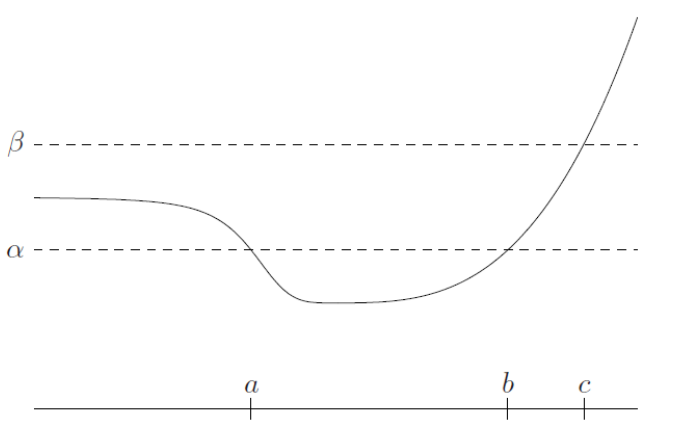
Threshold를 $\alpha$로 잡고 sublevel set을 구하면 $[a,b]$가 되겠네요. $[a,b]$는 convex set입니다.
마찬가지로 Threshold를 $\beta$로 잡고 sublevel set을 구하면 $(\infty ,c]$가 되겠네요.
$(\infty ,c]$는 당연히 convex set 입니다.
즉, quasiconvex function의 sublevel set은 구간이 된다고 생각해도 좋습니다.
함수 $f$가 quasiconvex 하면서 quasiconcave 하다면 함수 $f$를 quasilinear라고 부릅니다.
그다음으로는 Quasiconvex function이 기본적으로 가질 수 있는 성질들에 대해서 알아보도록 하겠습니다.
일단 quasiconvexity는 convexity의 조금 더 일반적인 버전이기 때문에 convexity가 가지는 성질들과 비슷한 성질들을 가지게 됩니다.
물론 둘이 동일하지는 않겠지만요.
- $f\left( \theta x+\left( 1-\theta \right) y\right) \leq \max\left\{ f(x),f(y)\right\}$
즉, line segment에 해당하는 함수 값이 end point의 최댓값을 넘을 수 없다는 것입니다.
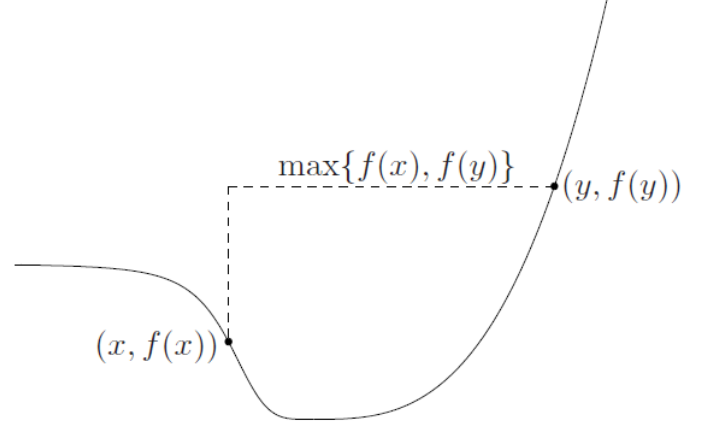
Convex function의 경우에는 $f\left(\theta x+\left(1-\theta \right)y\right) \leq \theta f(x)+(1-\theta )f(y), \; \theta \in [0,1] $
즉, end point들의 평균을 넘을 수 없었는데 이제는 그 조건이 end point의 최댓값으로 변경되었습니다.
이는 quasiconvex function의 정의를 잘 곱씹어보면 알 수 있습니다.
그렇기 때문에 quasiconvex function은 concave 할 수 있고, discontinous 할 수 있습니다.
그리고 임의의 함수 $f$가 정의역에서 연속함수이고, 일변수 함수($\mathbb{R}\rightarrow \mathbb{R}$)일 때, 아래의 성질을 하나라도 만족하면 quasiconvex function이라고 얘기할 수 있습니다.
- $f$ is non-decreasing
- $f$ is non-increasing
- there is a point $c \in \text{dom}(f)$ such that for $t \leq c$ (and $t \in \text{dom}f$), $f$ is nonincreasing, and for $c\leq t$ (and $t \in \text{dom}(f)$), $f$ is nondecreasing
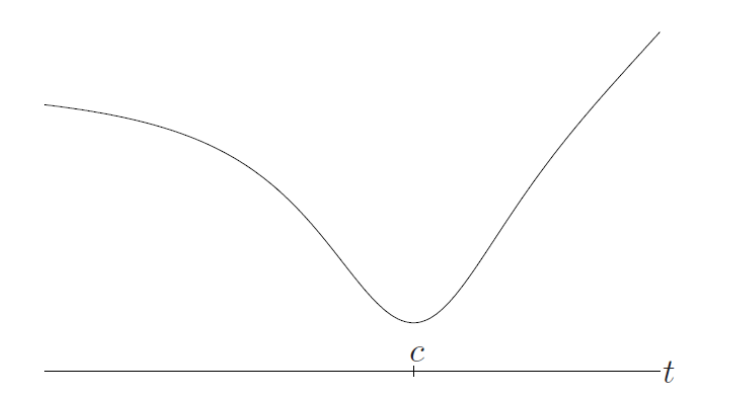
$c$를 기점으로 함수 $f$의 증감이 바뀌는 것을 볼 수 있습니다.
함수 $f$가 quasiconvex 라면 point $c$는 global minimizer이고, 이는 quasiconvex function에서만 성립합니다.
The first-order condition for quasiconvexity
Convex function에서의 first-order condition은 테일러 1차 근사가 global underestimator로 작용한다는 것입니다.
Quasiconvex function에서 이는 성립하지 않고 대신에 비슷하면서도 다른 condition을 가지게 됩니다.
임의의 함수 $f$가 일차 미분이 가능할 때, 함수 $f$가 quasiconvex function이 되기 위한 필요충분조건은 아래와 같습니다.
- $f(y)\leq f(x) \Longrightarrow \nabla f(x)^{\rm{T}}(y-x) \leq 0$
Convex function의 first-order condition은 $f(x)+\nabla f(x)^{T}(y-x)\leq f(y)$ 였습니다.
여기서 $\nabla f(x)=0$라면 Convex function에서는 global minimum이라는 것이 무조건 보장이 되었지만 quasiconvex function에서는 보장되지 않습니다.
이것이 가장 큰 차이점입니다. 그렇다면 Quasiconvexity의 first-order condtion을 같이 한번 증명해보도록 하겠습니다.
미분 가능한 함수 $f:\mathbb{R} \rightarrow \mathbb{R}$가 quasiconvex function이며 $\text{dom}(f)$ 역시 convex set이라 가정할 때
- $f(y)\leq f(x)\Longrightarrow f^{\prime }(x)(y-x) \leq 0$
이 정말 항상 성립하는지 알아보겠습니다.
일단 증명의 방향은 귀류법으로 진행됩니다. 반대의 상황을 가정하고 모순됨을 보이는 것이죠.
$x_{1}<x_{2}\Longrightarrow f(x_{2})\leq f(x_{1})$을 만족하는 $x_{1},x_{2}$이 있다고 가정하겠습니다.
그러고 나서 우리가 보이고 싶은 것은 다음과 같습니다.
$f(z)\leq f(x_{1}),z\in [x_{1},x_{2}]$ 왜냐하면 quasiconvex function이라면 $z\in [x_{1},x_{2}]$에 대해서 $f(z)$가 $[x_{1},x_{2}]$내의 최댓값인 $f(x_{1})$를 넘어설 수 없기 때문이죠.
이때 우리는 $f(x_{1})<f(z)$을 만족하는 $z$가 있다고 가정해보겠습니다.
Quasiconvexity에 위배되는 $z$라 보면 됩니다.
이때 함수 $f$가 미분 가능한 함수이기 때문에 $f^{\prime }(z)<0$를 만족하는 $z$를 찾을 수 있습니다.
하지만 $f(x_{1})<f(z)$에 대해 first-order condition에 대입을 한다면
- $f^{\prime }(z)(x_{1}-z)\leq 0$
이때 모순이 발생합니다. $(x_{1}-z)$가 항상 음의 값을 가지기 때문에 $0<f^{\prime }(z)$이 성립해야 하지만 이것은 우리가 선택한 $f^{\prime }(z)<0$에 모순되는 상황이기 때문입니다.
따라서 $f(x_{1})<f(z)$을 만족하는 $z$는 존재하지 않습니다.
따라서 quasiconvexity에 대한 first-order condition이 증명이 되었습니다.
The second-order condition for quasiconvexity
Quasiconvex function의 second order condition을 해석하는 것은 조금 어렵습니다.
우선 second-order condition부터 알아보겠습니다.
임의의 함수 $f:\mathbb{R}^{n}\rightarrow \mathbb{R}$가 quasiconvex function이며 두 번 미분이 가능하다면 아래의 부등식이 성립합니다.
- $y^{T}\nabla f(x)=0\Longrightarrow y^{\rm{T}}\nabla^{2} f(x)y \geq 0$
Convex function의 second-order condition은 함수 $f$의 hessian이 항상 positive semidefinite라는 점이었습니다.
Quasiconvex function의 second-order condition은 함수의 일차 미분이 0일 때 ($\nabla f(x)=0$), 이차 미분은 항상 양의 값을 가진다는 점입니다.
그렇다면 $\nabla f(x) \neq 0$인 곳에서는 어떠할까요?
책에 간단히 나와있지만 저는 이해하지 못하여 책에 나와있는 내용만을 그냥 그대로 적어보았습니다.
$n-1$차원에 대해서는 $\nabla^{2} f(x)$이 항상 positive semidefinite라고 합니다.
또한 이것이 의미하는 것은 $\nabla^{2} f(x)$ 적어도 하나 negative eigenvalue를 가진다는 것을 의미합니다.
Quasiconvexity에 대해서 역도 성립합니다.
$y^{T}\nabla f(x)=0\Longrightarrow y^{\rm{T}}\nabla^{2} f(x)y \geq 0$ 조건을 만족하면 함수 $f$는 Quasiconvex function이라는 것입니다.
Operations that preserve quasiconvexity
Quasiconvexity를 보존하는 연산들은 convexity를 보존하는 연산들과 비슷하지만 아예 동일하지는 않습니다.
간단하게만 살펴보고 마무리하도록 하겠습니다.
- Nonegative weighted maximum은 quasiconvexity를 보존합니다. 즉, $f=\max\left\{ w_{1}f_{1},\ldots ,w_{n}f_{n}\right\}$역시 quasiconvex function이라는 의미입니다. sum이 아닌 이유는 quasiconvex function끼리 더하는 연산이 quasiconvexity를 보존하기 못하기 때문입니다.
- 만약 $g:\mathbb{R}^{n}\rightarrow \mathbb{R}$가 quasiconvex function이고 $h:\mathbb{R}\rightarrow \mathbb{R}$가 단조 증가함수라면 $f=h\circ g$ 역시 quasiconvex function입니다.
- $f(Ax+b),f(\frac{Ax+b}{c^{\rm{T}}x+d} )$ : Affine function이나 linear-fractional transformation이 적용된 composition 역시 quasiconvexity를 보존합니다.
- $g(x)=\inf_{y\in C} f(x,y)$ 역시 quasiconvexity를 보존합니다.
Quasiconvexity를 보존하는 연산은 또한 convexity를 보존할 수 있습니다.
하지만 convexity를 보존하는 연산은 quasiconvexity를 보존할 수 없습니다.
Quasiconvex function이 좀 더 general 함수이기 때문입니다.
Conclusion
지금까지 2번의 포스팅을 통해 convex function의 정의, 성질, 관련 연산들에 대해서 알아보았습니다.
다음 글부터는 본격적으로 convex optimization에 대해서 알아보도로 하겠습니다.
감사합니다.
'Math > Convex Optimization' 카테고리의 다른 글
| Optimization Theory (Gradient Descent - Convergence Analysis) (2) | 2022.09.08 |
|---|---|
| Optimization Theory (Unconstrained Optimization) (0) | 2022.09.08 |
| Optimization Theory (Convex Optimization Problems) (0) | 2022.05.03 |
| Optimization Theory (Convex Functions Ⅰ) (1) | 2022.04.23 |
| Optimization Theory (Convex Sets) (0) | 2022.04.23 |



