Optimization Theory (Convex Functions Ⅰ)

Convex Function 역시 Convex Set과 비슷하게 정의를 먼저 살펴보고, 다양한 예시 그리고 Convexity를 보존하는 연산들을 살펴볼 것입니다.

 

추가로 Quasiconvex function과 log convex function에 대해서도 알아보도록 하겠습니다.

Lecture 3 : Convex Functions

Basic properties and examples

Convex functions

 

우선 Convex function의 정의부터 알아보도록 하겠습니다. 우선 함수가 정의되는 정의역이 convex set 이어야 합니다. 그러한 상태에서 다음의 부등식을 만족하는 함수를 우리는 convex function이라 정의합니다.

 

• $f(\theta x+(1-\theta )y)\leq \theta f(x)+(1-\theta )f(y),0\leq \theta \leq 1$

여기서 등호가 사라지면 우리는 strictly convex function이라 정의합니다.

 

• $f(\theta x+(1-\theta )y)<\theta f(x)+(1-\theta )f(y),0\leq \theta \leq 1$

$\theta x+(1-\theta )y$는 $x$와 $y$사이에 존재하는 정의역입니다. 거기에 대응되는 치역이 $f(\theta x+(1-\theta )y)$ 입니다.

 

$\theta f(x)+(1-\theta )f(y)$는 $f(x)$와 $f(y)$의 line segment입니다. 그래프로 보면 $f(x)$와 $f(x)$를 이어주는 선분으로 보면 됩니다.

 

이때, 저 부등식이 의미하는 것은 함수의 두 point로부터 만들어지는 line segment는 항상 함수의 값보다 크거나 작다라는 의미입니다. 아마 직관적으로 다들 이해할 수 있을 것 같습니다. 꼭 저렇게 접시모양처럼 둥글 필요는 없지만 양의 곡률을 가져야 합니다.

 

임의의 함수 $f$가 convex라면 -f는 concave(오목)라고 정의합니다. 그래서 모든 affine function은 convex 하면서 concave 합니다. 직선을 예시로 상상해보면 convex, concave 성질을 둘 다 만족하기 때문입니다. 그 역도 성립합니다. 임의의 함수가 convex 하면서 concave 하다면 그 함수는 affine function이라 볼 수 있습니다.

 

함수가 Convex 함을 알 수 있는 또 다른 접근이 있습니다. 함수가 정의되는 정의역에서 임의의 Point에 대해 특정 방향으로 Linear 한 직선을 그었다고 가정했을 때, 그 도메인에 대응되는 함수의 치역들이 만들어내는 단면이 생기게 됩니다. 이때 그 단면이 convex 하고 이것이 domain에 있는 모든 point에 대해 어떤 방향으로 움직이든 간에 성립이 된다면 그 함수는 convex function이라는 것입니다.

 

• $g(t)=f(x+tv),\{ t|x+tv\in domf\} $ : 이때 $g(t)$가 $t$에 대해서 convex 하다면 원래 함수 $f$ 역시 convex 한다는 의미입니다.

내용이 어려우니, 제가 그려본 간단한 예제를 같이 보도록 하겠습니다.

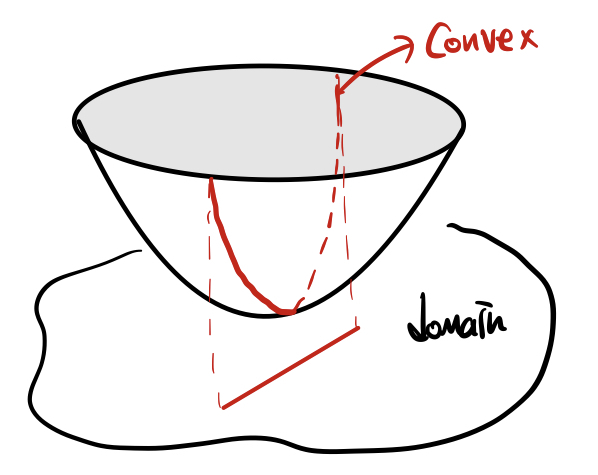
domain에서 어떻게 line을 그어도 거기에 해당되는 함수의 단면이 convex 하다면 그 함수는 convex 하다고 볼 수 있습니다.

 

일단 이렇게 해서 Convex Function의 정의에 대해서 알아봤습니다.

 

First-order conditions

 

임의의 함수 $f$가 Convex 하고 1차 미분이 가능하다면, 꽤나 좋은 성질을 가지게 됩니다. 함수의 하한을 무조건 찾을 수 있기 때문입니다. 때때로 어떤 함수의 lower bound를 찾는 것이 어려울 수 있습니다. 하지만 함수가 Convex 하고 일차 미분이 가능하다면 1차 테일러 근사를 통해서 global underestimator를 얻을 수 있는 것이지요.

 

• $f(x)+\nabla f(x)^{T}(y-x)\leq f(y)$

위의 부등식을 얻을 수 있는데 이는 함수의 lower bound를 보장해주는 부등식이라 볼 수 있습니다. (n=1)이라면 우리가 잘 알고 있는 일변수 형태의 $f(x)+f^{\prime }(x)(y-x)\leq f(y)$ 익숙한 부등식을 얻을 수 있습니다.

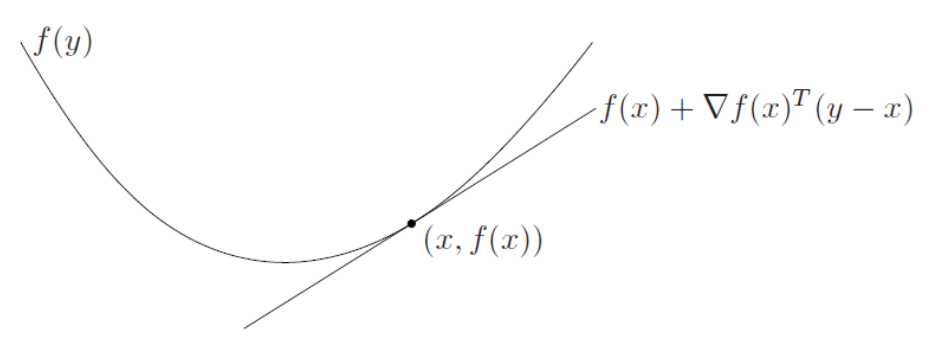
그림을 보면 알겠지만 $x$라는 포인트에서 일차 테일러 근사를 구했을 때, 그 근사치는 항상 원래 함수보다 작다는 것을 알 수가 있습니다. 아직 convex optimization에 대해서 자세히 공부를 한 것은 아니지만, 책에서는 이 일차 미분 성질이 convex function의 아주 중요한 성질이라고 강조를 하고 있습니다. 임의의 함수가 Convex function이라면 $\nabla f(x)=0$이 global minimum이기 때문이죠.

 

중요한 성질인 만큼 증명도 같이 한번 해보고 넘어가도록 하겠습니다. 우리가 증명하고 싶은 명제는 다음과 같습니다.

 

" 미분 가능한 Convex 한 함수는 $f(x)+\nabla f(x)^{T}(y-x)\leq f(y)$를 만족한다."

 

정말로 그러한지 보도록 하겠습니다. 간단하게만 진행하기 위해 (n=1)인 일변수 함수에 대해서만 해보도록 하겠습니다.

먼저 $f$가 convex 하므로 우리는 아래의 부등식을 얻을 수 있습니다.

 

• $f(tx+(1-t)y)\leq tf(x)+(1-t)f(y),0\leq t\leq 1$

여기서 양변을 $t$로 나눠주고 이항을 조금 해주면 아래처럼 만들 수 있습니다.

 

• $f(x)+\frac{f(x+t(y-x))-f(x)}{t} \leq f(y)$

여기서 $t\rightarrow 0$ 극한을 취해주면

 

• $f(x)+(y-x)\lim_{t\rightarrow 0} \frac{f(x+t(y-x))-f(x)}{t(y-x)} \leq f(y)\Longrightarrow f(x)+f^{\prime }(x)(y-x)\leq f(y)$

원래 일차 미분 부등식을 얻을 수 있습니다. f가 convex 하다면 이 부등식을 유도할 수 있으니, 이제는 반대로 이 부등식을 가지고 f가 정말 convex 한지 알아보도록 하겠습니다. $x!=y,0\leq \theta \leq 1,z=\theta x+(1-\theta )y$를 가정했을 때 두 가지 부등식을 얻을 수 있습니다.

 

• $f(z)+(x-z)f^{\prime }(z)\leq f(x)$ ... (1)
• $f(z)+(y-z)f^{\prime }(z)\leq f(y)$ ... (2)

여기서 첫 번째 부등식에는 $\theta$를 두 번째 부등식에는 $1-\theta $를 곱해주고 각자 더해주면 아래의 결과를 얻을 수 있습니다.

 

• $\theta f(z)+\theta (x-z)f^{\prime }(z)+(1-\theta )f(z)+(1-\theta )(y-z)f^{\prime }(z)\leq \theta f(x)+(1-\theta )f(y)$

• $f(z)(\theta +1-\theta )+f^{\prime }(z)(\theta x-\theta z+y-z-\theta y+\theta z)\leq \theta f(x)+(1-\theta )f(y)$

• $f(z)=f\left( \theta x+(1-\theta )y\right)  \leq \theta f(x)+(1-\theta )f(y)$

부등식을 다 정리해보면 우리가 알고 있는 Convex Function의 정의를 띠고 있습니다. 고로 증명이 완료되었습니다.

 

Second-order conditions

 

임의의 함수 $f$가 Convex 하고 2차 미분이 가능하다면(Hessian Matrix가 존재) 함수의 2차 미분이 모든 정의역에 대해 항상 양의 값을 가진다면 임의의 함수는 Convex Function이라 할 수 있다입니다. 그 역도 성립합니다.

 

조금 더 간단하게 생각해보겠습니다. 우리가 고등학교 때 수학 시간 때 미적분을 잘 배웠다면 함수가 아래로 볼록하기 위해서는

 

• $0\leq f^{\prime \prime }(x)$

라는 조건이 필요했습니다. 이계도함수가 항상 양수라는 것은 함수의 도함수는 단조 증가한다는 의미입니다. 도함수가 단조 증가하기 위해서는 아래의 그림과 같은 그래프의 모양이어야 합니다.

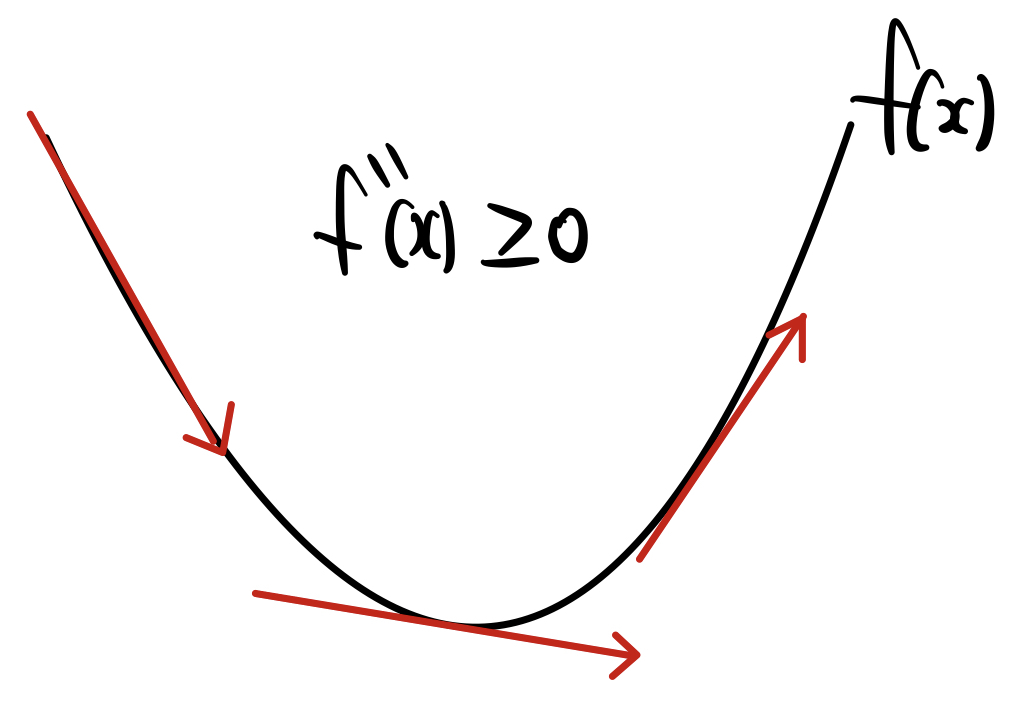
같은 맥락입니다. n=1이 아닌 경우의 함수의 이차 미분은 Hessian Matrix를 통해 얻을 수 있을 것입니다.

 

• $0\preceq \nabla^{2} f(x)$

즉, 임의의 함수 $f:R^{n}\rightarrow R$의 Hessian Matrix가 Positive semi definite라면 함수 $f$는 Convex 합니다. 역도 성립하기 때문에 이 성질을 이용하여 우리는 처음 보는 함수의 Convexity를 증명하는 데 사용할 수 있습니다.

 

사실 Hessian Matrix를 구하는 것은 단순 미분이기 때문에 어렵지는 않지만 그 Hessian이 Positive semi definite라는 것을 보이는 것은 쉽지 않기 때문에 상황에 따라 사용하면 됩니다.

 

참고로 Hessian Matrix가 Positive definite라면 함수 $f$는 strictly convex입니다. 하지만 이 경우에는 역은 성립하지 않습니다.

 

증명은 따로 책에 나와있지 않고 연습문제에 있다고 하여, 이번 글에서는 다루지 않겠습니다.

 

Examples of convex functions

 

이번에는 다양한 convex function들의 convexity를 증명해보도록 하겠습니다.

다양한 예제들을 바로 증명하기 이전에 Convex Function들의 Convexity는 어떻게 증명하는지 알아보겠습니다.

 

• $f\left( \theta x+(1-\theta )y\right)  \leq \theta f(x)+(1-\theta )f(y)$ : Convex function의 정의를 이용

• $0\preceq \nabla^{2} f(x)$ : second-order condition을 이용하는 것입니다. 역이 성립하기 때문에 Hessian이 Positive semidefinite라면 f는 convex입니다.

• $g(t)=f(x+tv),\{ t|x+tv\in domf\} $ : 함수가 정의되는 정의역에서 임의의 Point에 대해 특정 방향으로 Linear 한 직선을 그었을 때 대응되는 치역들이 convex 함을 보이는 것입니다. 자주 사용되지는 않는다고 합니다.

Convexity를 증명하는 데 있어서는 왕도가 없다고 합니다. 문제마다 다르고 하나씩 다 해봐야 하는 부분이라고 합니다. 아무튼 하나씩 풀어보도록 하겠습니다.

비교적 간단한 예시입니다. Convex function의 정의와 삼각 부등식을 이용하여 증명해보도록 하겠습니다.

 

• $f(\theta x+(1-\theta )y)\leq f\left( \theta x\right)  +f((1-\theta )y)$

Norm은 삼각 부등식을 만족하기 때문에 위의 부등식이 성립합니다. ($\sqrt{x^{2}+y^{2}} \leq \sqrt{x^{2}} +\sqrt{y^{2}} $)

 

• $f\left( \theta x\right)  +f((1-\theta )y)=\theta f(x)+(1-\theta )f(y)$

Norm은 homogeniety 성질을 만족하기 때문에 결국 $f\left( \theta x+(1-\theta \right)  y)\leq \theta f(x)+(1-\theta )f(y)$가 성립됩니다.

 

고로 모든 norm 함수는 convex function입니다.

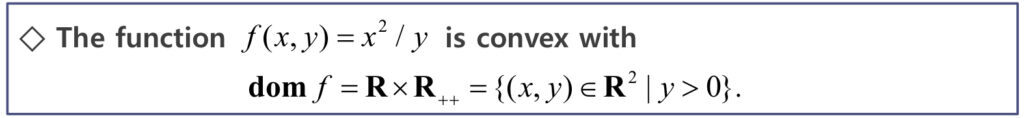
$x$와 $y$를 독립변수로 가지는 다변수 함수 $f(x,y)=\frac{x^{2}}{y} $ 입니다. 정의를 이용해서 증명해 보이기엔 어려워 보입니다. 다변수 함수이기에 Hessian Matrix를 통한 second-order condition으로 접근해보도록 하겠습니다.

 

• $\nabla^{2} f(x,y)=\left[ \begin{matrix}\frac{\partial^{2} f}{\partial x^{2}} &\frac{\partial^{2} f}{\partial x\partial y} \\ \frac{\partial^{2} f}{\partial y\partial x} &\frac{\partial^{2} f}{\partial y^{2}} \end{matrix} \right]  $

열심히 미분을 수행해서 계산을 해주면 구할 수 있습니다.

 

• $\nabla^{2} f(x,y)=\frac{2}{y^{3}} \left[ \begin{matrix}y^{2}&-xy\\ -xy&x^{2}\end{matrix} \right]$

여기서 $y$는 항상 양의 값을 가지기 때문에 $\frac{2}{y^{3}}$는 신경 쓸 필요가 없습니다. Hessian을 구하는 것은 어렵지 않지만 이 행렬이 Positive Semidefinite라는 것을 증명하기 위해서는 몇 가지 테크닉이 필요하죠.

 

• $\nabla^{2} f(x,y)=\frac{2}{y^{3}} \left[ \begin{matrix}y^{2}&-xy\\ -xy&x^{2}\end{matrix} \right]  =\frac{2}{y^{3}} \left[ \begin{matrix}y\\ -x\end{matrix} \right]  \left[ \begin{matrix}y\\ -x\end{matrix} \right]^{T}  $

우선 행렬을 열벡터와 행벡터의 곱으로 분해할 수 있습니다.

 

그래서 우리의 Hessian을 $H=hh^{T}$ 이렇게 표현할 수 있습니다. 이때, 임의의 벡터 $x$에 대해 $0\preceq x^{T}(hh^{T})x$가 성립하면 $H$는 positive semidefinite입니다.

 

• $x^{T}(hh^{T})x=x^{T} hh^{T} x=(x^{T} h)^{2}$

결국 저렇게 제곱의 항으로 묶을 수 있으니 항상 양수라는 것이 보장됩니다. 고로 Hessian이 Positive Semidefinite이며 함수 $f(x,y)$는 Convex function 입니다.

다음으로는 log-determinant입니다. $S^{n}_{++}$라는 말은 symmetric positive definite라는 의미입니다. 여기서 $f(x)$의 convexity를 증명하기 위해 우리는 $g(t)=f(Z+tV),0\prec Z+tV$를 정의해보도록 하겠습니다. 여기서 $Z+tV$는 line은 아니겠지만 선형적인 어떤 공간을 가진다고 생각하면 되겠습니다.

 

• $g(t)=log\left( det\left( Z+tV\right)  \right)  $

이때, $g(t)$가 $t$에 대해 concave 하다면 $f(x)$는 $X$에 대해서 concave 하다고 볼 수 있습니다. 고로 $g(t)$가 $t$에 대해 concave 함을 보이면 증명이 완료될 것 같습니다.

 

• $g(t)=log\left( det\left( Z+tV\right)  \right)  =log(det\left( Z^{1/2}(I+tZ^{-1/2}VZ^{-1/2})Z^{1/2}\right)$

갑자기 뭔가 수식이 복잡해졌습니다. 행렬 연산을 통해서 항등식을 만들어준 것입니다. 행렬 연산을 진행할 때 $A(B+C)A=ABA+ACA$가 성립합니다. 이러한 관점이면 수식이 둘 다 동일하다는 것을 알 수 있습니다. determinant는 곱하기에 대해서 이동할 수 있으니 그 성질을 이용하기 위해 행렬들의 곱으로 분해했다고 생각하면 됩니다.

 

• $log(det\left( Z^{1/2}(I+tZ^{-1/2}VZ^{-1/2})Z^{1/2}\right)  =log(det\left( (I+tZ^{-1/2}VZ^{-1/2})Z\right)  $

그리고 determinant의 성질을 이용해 분리를 하겠습니다.

 

• $log(det\left((I+tZ^{-1/2}VZ^{-1/2})Z\right))=log(det\left( I+tZ^{-1/2}VZ^{-1/2}\right)det\left( Z\right))$

log에서의 곱셈은 덧셈으로 분리할 수 있는 성질이 있습니다. 그것을 이용해서 수식을 전개하겠습니다.

 

• $log(det\left(I+tZ^{-1/2}VZ^{-1/2}\right)det\left( Z\right))=log\left(det\left( I+tZ^{-1/2}VZ^{-1/2}\right)\right)+log(det(Z))$

여기서 $Z^{-1/2}VZ^{-1/2}=Y$라고 치환하도록 하겠습니다.

 

• $g(t)=log(det(I+tY))+log(det(Z))$

이때 Y에 고유값 분해를 해보도록 하겠습니다. $Y=U\Lambda U^{-1}$

 

• $log(det(I+tU\Lambda U^{-1}))=log(det(U(I+t\Lambda )U^{-1}))$

동일하게 행렬 연산을 통해서 곱으로 묶어주었습니다. 이제 determinant 성질을 이용하여 수식을 정리하면

 

• $log(det(U(I+t\Lambda )U^{-1}))=log\left(det\left( I+t\Lambda \right)\right)$

고유값 분해를 했을 때는 $UU^{-1}=I$이 성립하기 때문입니다.

 

• $g(t)=log(det\left(I+t\Lambda )\right)  +log(det(Z))$

여기서 $I$와 $t\Lambda$는 대각 행렬입니다. 그 행렬의 덧셈인 $I+t\Lambda$도 대각 행렬이겠죠. 대각 행렬의 determinant는 대각 성분의 곱셈으로 이루어집니다. 그리고 log내부의 곱셈은 log끼리의 덧셈으로 변환이 됩니다. 이 성질들을 이용해보겠습니다.

 

• $log(det\left( I+t\Lambda )\right)  =log\left( \prod^{n}_{i=1} \left( 1+t\lambda_{i} \right)  \right)  =\sum^{n}_{i=1} log\left( 1+t\lambda_{i} \right)$

이제 $g(t)$를 정리해보도록 하겠습니다.

 

• $g(t)=\sum^{n}_{i=1} log\left( 1+t\lambda_{i} \right)  +log\left(det\left( Z\right)\right)$

그리고 난 다음에 $g(t)$를 $t$에 대해서 미분을 하면

 

• $g^{\prime }(t)=\sum^{n}_{i=1} \frac{\lambda_{i} }{\left( 1+t\lambda_{i} \right)  } ,g^{\prime \prime }(t)=-\sum^{n}_{i=1} \frac{\lambda^{2}_{i} }{\left( 1+t\lambda_{i} \right)^{2}  } $

최종적으로 $g^{\prime \prime }(t)\leq 0$가 항상 성립하기 때문에 $g(t)$는 $t$에 대해서 concave function이고 이로 인해 $f$ 역시 concave function이라는 것이 증명되었습니다.

 

예제를 풀어보는 것은 이 정도로 마무리하도록 하겠습니다.

 

Sublevel sets, superlevel sets and epigraph

 

Sublevel set의 정의는 다음과 같습니다. $C_{\alpha }=\{ x\in domf|f(x)\leq \alpha \} $ 입니다. 일정 threshold보다 작은 정의역들의 집합이라 보면 됩니다. 이것을 Sublevel set이라 정의합니다. 이때, Convex function의 Sublevel set은 Convex set이라는 사실을 알 수 있습니다.

 

$x,y\in C_{\alpha }$를 가정해보겠습니다. 이때, $f(x)\leq \alpha ,f(y)\leq \alpha $ 성립하기 때문에 당연히 $f(\theta x+(1-\theta )y)\leq \alpha $가 성립합니다. 그렇기 때문에 $\theta x+(1-\theta )y\in C_{\alpha }$ 성립하며 $C_{\alpha}$는 Convex Set입니다.

 

하지만 역은 성립하지 않습니다. $f(x)=-e^{x}$의 sublevel set은 항상 convex set이지만, $f(x)=-e^{x}$는 convex function이 아닙니다.

 

Sublevel set의 특성은 때때로 특정 집합의 convexity를 증명하는 데 있어 좋은 성질이 될 수 있습니다.

Superlevel set은 그 반대라 생각하면 됩니다. $C_{\alpha }=\{ x\in domf|\alpha \leq f(x)\} $로 일정 threshold보다 큰 정의역들의 집합이라 보면 됩니다.

 

이것을 Superlevel set이라 정의합니다. 비슷하게 Concave function의 superlevel set은 convex set입니다. 동일하게 역은 성립하지 않습니다.

 

epigraph와 hypograph에 대해서도 알아보겠습니다.

 

epigraph는 그래프의 위쪽을 의미합니다. 정의는 다음과 같습니다.

 

• $epif=\left\{ \left( x,t\right)  |x\in domf,f(x)\leq t\right\}  $

이 epigraph를 통한 convex function의 성질이 있습니다. "어떤 임의의 함수의 epigraph가 convex function이라는 것은 임의의 함수 f가 convex function이기 위한 필요충분조건이다" 입니다.

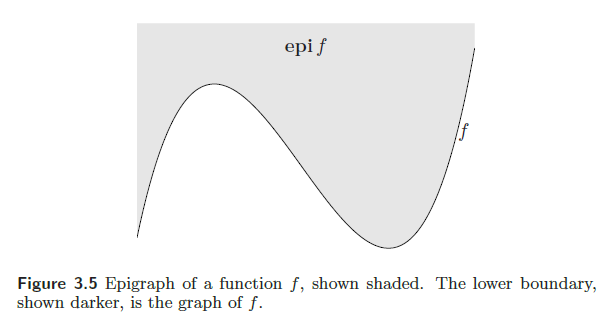
hypograph는 그래프의 아래쪽을 의미합니다. 정의는 다음과 같습니다.

 

• $epif=\left\{ \left( x,t\right)  |x\in domf,t\leq f(x)\right\}$

비슷하게 hypograph를 통한 concave function의 성질이 있습니다. "어떤 임의의 함수의 hypograph가 convex function이라는 것은 임의의 함수 f가 concave function이기 위한 필요충분조건이다"입니다.

 

Jensen's inequality

 

마지막으로 알아볼 것은 Jensen's inequality입니다. 우선 Convex function의 정의를 다시 한번 떠올려 보겠습니다. $f\left( \theta x+\left( 1-\theta \right)  y\right)  \leq \theta f(x)+(1-\theta )f(y)$로 두 점에 대해서만 고려를 하였습니다. 하지만 두 점 이상의 convex combination으로 확장한다면 Jensen's inequality를 얻을 수 있습니다.

 

임의의 함수 $f$가 convex function 일 때, $x_{1},\ldots ,x_{k}\in domf$ 그리고 $0\leq \theta_{1} ,\ldots ,\theta_{k}$  일 때 $\theta_{1} +\ldots +\theta_{k} =1$를 만족한다면 아래의 부등식이 성립합니다.

 

• $f(\theta_{1} x_{1}+\ldots \theta_{k} x_{k})\leq \theta_{1} f(x_{1})+\ldots \theta_{k} f(x_{k})$

기댓값의 볼록 함수와 볼록 함수의 기댓값 사이에 성립하는 부등식으로 통계학에서는 정말 많이 사용되는 부등식이라고 합니다. multiple point를 무한개로 늘린다면 적분으로 부등식을 변환할 수 있습니다.

 

• $f(\int_{S} p(x) x\cdot dx)\leq \int_{S} f(x)p(x)\cdot dx$

적분 형태로 표현할 수 있지만 기댓값의 형태로도 표현할 수 있죠.

 

• $f(E(x))\leq E(f(x))$

아직 통계이론과 최적화 이론은 잘 모르기 때문에 Jensen inequality의 중요성에 대해서는 잘 모르지만 많이들 사용되며 증명과정에 있어 유용하다고 합니다.

 

이상으로 Convex Function에 대해서 알아보았습니다. 다음 글에서는 Convex Function의 convexity를 보존하는 연산들 그리고 Quasiconvex function에 대해서 알아보도록 하겠습니다.

 

감사합니다.