Intro
이제 본격적으로 convex optimization에 대해서 알아보도록 하겠습니다.
이전까지는 convex set이 무엇인지 그리고 convex function이 무엇인지 알아보는 과정을 거쳤습니다.
그러한 지식을 바탕으로 이제 최적화가 무엇이고 그중 convex optimization이 무엇인지 알아보도록 하겠습니다.
일단 이번 포스팅에서는 문제가 어떻게 정의되는지 정도로만 얘기할 것입니다.
Convex Optimization Problems
1. Optimization problems
그렇다면 일단 최적화 문제가 무엇인지 알아보는 것부터 시작하겠습니다. 여기서 general 한 optimization의 형태는 아래와 같습니다.
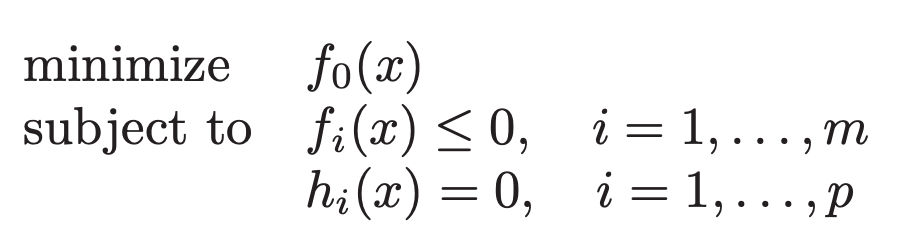
일단 우리의 목적함수(objective function) 혹은 비용 함수(cost function) $ f_{o}(x)$가 존재합니다.
그래서 보통 최적화는 이 목적함수를 최소화하는 $ x $를 찾는 것이 목표인데, 이 $ x $는 constraints를 만족해야 합니다.
즉, constraints는 optimization 변수 $ x $가 만족해야 하는 조건이라 보면 됩니다.
- $ f_{i}(x)\leq 0, i=1,\ldots , m $는 inequality constraints라고 정의합니다.
- $ h_{i}(x)=0, i=1,\ldots , p $는 equality constraints라고 정의됩니다.
그래서 optimization problem에 모든 constraints를 만족하는 집합을 feasible set이라고 정의합니다.
$ \mathcal{D}=\bigcap^{m}_{i=1} \text{dom}(f_{i}) \cap \bigcap^{p}_{i=1} \text{dom}(h_{i})$이 feasible set이 되겠네요.
그리고 이 feasibile set이 optimization problem의 정의역이 되는 것입니다.
그리고 우리의 목적은 optimization problem에 해당하는 최적의 솔루션(optimal value)을 찾는 것입니다.
- $ p^{\ast }=\inf\left\{f_{o}\left(x\right) | f_{i}\left(x\right)\leq 0, i=1,\ldots, m, h_{i}\left(x\right)=0, i=1,\ldots , p\right\}$
그리고 이 최적의 솔루션은 여러 개일 수 있습니다.
다음으로는 극소점(locally optimal)에 대해서 알아보도록 하겠습니다.
극소점은 그 지역에서만 optimal 한 값으로 작은 반경 $R$ 에 대해서는 가장 작은 값을 가지는 point라 보시면 됩니다.
- $ f_{o}\left( x\right)=\inf \left\{f_{o}\left(z\right) \,|\,f_{i}\left(z\right)\leq 0, i=1,\ldots , m, h_{i}\left(x\right)=0 , i=1,\ldots , p,\| z-x\|_{2}\leq R\right\}$

그래서 지금까지 일반적인 최적화 문제는 어떻게 정의가 되는지 알아봤습니다.
일반적인 최적화 문제는 그 문제가 feasible 한지 아닌지 알아봐야 하는데요.
무슨 소리냐면 Constraints를 만족하는 $ x $가 있는지 없는지 확인해야 한다는 의미 입니다.
일반적인 최적화 문제에서는 feasible set이 공집합일 수 있다고 합니다. 즉 해가 없다는 문제라는 소리겠죠.
그래서 constraints를 만족하는 $ x $가 하나라도 존재한다면 그 문제는 solvable problem이 되는 것이고 아니면 insolvable problem이 되는 것입니다.
당연히 앞으로의 내용은 feasible set이 존재하는 문제에 대해서 다룰 예정입니다.
2. Equivalent problems
이제 최적화 문제 중 equivalent problem에 대해서 알아보도록 하겠습니다.
Equivalent problem이란 서로 다른 두 최적화 문제가 서로 같은 해를 가진다는 문제입니다.
그래서 어떻게 활용될 수 있나면 우리가 잘 알고 있고 풀기 쉬운 문제로 해를 먼저 찾고 이 쉬운 문제와 equivalent 한 관계에 있는 문제에 대입해서 바로 해를 찾을 수 있다는 소리입니다.
쉬운 문제로 정답을 찾고 다른 문제에 접근하는 방식인데 여기서 중요한 것은 두 문제가 equivalent라는 것이 증명이 되어야 한다는 것입니다.
그래서 equivalent problem을 만들어내는 몇 가지 transformation이 존재하는 데 그것들에 대해서 같이 알아보겠습니다.
Change varialbes
변수 변환입니다. 일대일 대응 관계로 변수 변환 함수가 존재한다면 Optimization Problem의 해를 찾고 그 Optimal point를 일대일 대응 함수에 넣어서 새로운 해를 찾을 수 있겠죠. 최적화 변수를 새롭게 mapping 해주는 함수 $\phi (z)=x,\phi^{-1} (x)=z $만 찾을 수 있다면 가능한 방법입니다.

Transformation of objective and constraint functions
다음으로는 objective function과 constraint function을 조금 변형시키는 경우입니다. 이 목적함수를 변형시킬 때는 무조건 단조 증가(monotone increasing) 함수로 변형을 해야 합니다.
무슨 소리 나면 우리의 새로운 목적함수 $\tilde {f_{o}}(x)=\psi_{0}(f_{o}(x))$가 단조 증가함수라면 이 함수의 최소 지점은 정의역이 최소가 되는 부분입니다. 그리고 이 정의역이 최소가 된다는 것은 우리의 원래 목적함수를 최소화하는 것과 같은 맥락이죠.

Slack variables
Inequality constraints를 equality constraints로 만들어주는 것입니다. 원래 $ f_{i}(x)\leq 0 $는 $0\leq s_{i}$에 대해서 $ f_{i}(x)+s_{i}=0 $ 이렇게 equality constraints로 변경할 수 있습니다. 여유 변수를 새롭게 도입해서 inequality constraints를 equality constraints로 변경한 방식입니다.

Eliminating equality constraints
변수 변환과 더불어 equality constraints를 동시에 없애주는 방식입니다. 즉, 변수 변환 + $ h_{i}(x)=0 $을 동시에 만족시키는 매개 함수 $ x=\phi (x)$를 찾아주는 것이 핵심입니다. 그런데 이 $ x=\phi (x)$를 찾아주는 것이 쉽지는 않겠죠. 이렇게 해서 새롭게 equivalent 한 problem에는 inequality constraints만 존재하게 됩니다.

Eliminating linear equality constraints
자 여기서는 동일하게 equality constraints를 제거해주는 것이 목적인데, equality constraints가 Affine function 일 때의 경우입니다. 원래 original problem의 equality constraints를 $ Ax=b $라 하겠습니다.
그리고 임의의 행렬 $ F\in \mathbb{R}^{n\times k} , Range(F)=Null(A)$이 있다고 가정해보겠습니다. F의 Column space가 A의 Null Space에 해당하는 것이죠. 따라서 $ AFz=0 $이 성립합니다.
그러고 나서 원래 original problem의 equality constraints $ Ax=b $를 만족하는 $ x $를 $ x_{0}$라 가정하겠습니다. 이때 우리의 최적화 변수 $ x$를 $x=Fz+x_{0}$라고 두면 $A(Fz+x_{0})=0+b=b$가 항상 성립하기 때문에 equality constraints를 지워도 됩니다. 단 $F$ 를 잘 찾는 것이 중요하겠죠.

Optimizing over some variables
예를 들어 우리의 목적함수에 변수가 $x , y $만 존재한다고 가정하겠습니다. 이때 목적함수를 $ x, y $에 대해서 최적화시키는 것은 먼저 $ x $를 상수로 고정해놓고 $ y $에 대해서 최적화를 진행한 다음 $ x $로 최적화하는 것과 같은 이치입니다.
아래의 그림으로 먼저 감을 잡을 수 있는데요.
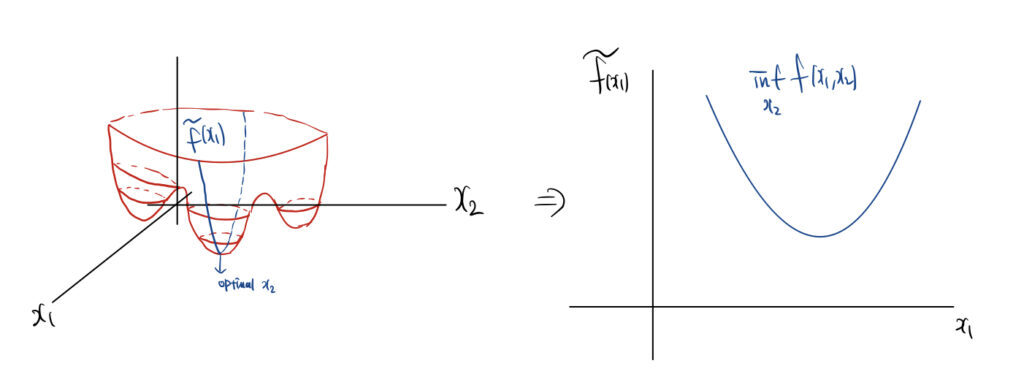
$ f(x_{1}, x_{2})$가 있을 때 우선 $ x_{1}$를 상수로 고정하고 최적의 $ x_{2}$를 찾은 다음 그 최적의 $ x_{2}$로 픽스를 시킨 $\tilde {f} (x_{1})$에 대해서 $ x_{1}$ 가지고 최적화를 진행하는 것입니다.

이와 비슷하게 작동하는 alternating optimization 기법이 있는데요. 그 방법은 global minima를 보장할 수 없다고 합니다. 이와 반대로 지금 설명한 방식은 global minima를 이론적으로 보장할 수 있다고 하네요.
Epigraph problem form
마지막으로 epigraph 형태로 문제를 변경할 수 있습니다.

자 문제가 $ f_{o}(x)\leq t $ 이렇게 있을 때 $ t $를 최소화하는 것은 $ f_{o}(x)$를 최소화하는 것과 같습니다.
3. Convex Optimization
위에서는 일반적인 최적화 상황에 대해서 다루었고 이제는 convex optimization에 대해서 얘기해보도록 하겠습니다. 이번 글에서는 간단히 소개 정도로만 할 것이고 다음 글에서 차차 구체적인 예시와 어떤 알고리즘들이 있는지 알아보도록 하겠습니다.
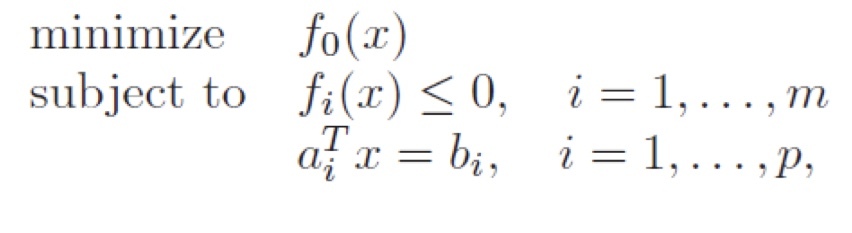
- 우선 목적함수 $ f_{o}(x)$가 convex function이어야 합니다.
- inequality constraints $ f_{i}(x)$ 역시 convex function이어야 합니다.
- equality constraints $ a^{\rm{T}}_{i} x-b_{i}=0 $는 affine function이어야 합니다.
- 마지막으로 feasible set이 convex set 이어야 합니다.
Concave maximization problem 역시 convex Optimization이라 볼 수 있습니다.
Global optimal = Locally optimal
Convex optimization이라는 것이 증명이 된다면 가장 중요한 성질이 있었죠.
Global Optimal을 무조건 구할 수 있다는 성질이 있었습니다.
Proof)
그렇다면 "Global optimal = locally optimal" 이 정말로 성립하는지 증명을 통해 알아보도록 하겠습니다.
우선 feasible point $ x $ 에 대해서 $ x $ 가 locally optimal point라 가정하겠습니다.
- $ f_{o}(x)=\inf \left\{ f_{o}\left( z\right)\,|\, \text{z is feasible},\,\| z-x\|_{2} < R\right\},\, \text{for some}\, R>0 $
그런데 여기서 $ x $는 locally optimal이지, global optimal이 아니라고 가정해보겠습니다. 그리고 우리는 이 가정이 모순이라는 것을 밝혀서 결국 "Global optimal = locally optimal"라는 것을 밝히도록 하겠습니다.
새로운 $ y $ 를 등장시키도록 하겠습니다. 이 $ y $ 를 우리는 global optimal이라 정의하겠습니다.
그러므로 아래의 부등식이 성립합니다.
- $ f_{o}(y)<f_{o}(x)$
그런데 이때 $ x $와 $ y $의 거리는 $ R $ 보다 커야 합니다. 만약에 $ R $ 보다 작다면 $ x $ 가 극소점이라는 가정에 위배되기 때문입니다.
- $\|y-x\|_{2} > R $
그리고 이 상황에서 $ x $ 와 $ y $ 사이에 있는 $ z=\left( 1-\theta \right) x+\theta y,\, \theta \in [0,1]$ 를 고려하면서 정확히 $ x $ 와 $ y $ 절반에 위치하도록 $\theta =\frac {R}{2\| y-x\|_{2} } $ 를 이렇게 정의해주겠습니다.
- $\| z-x\|_{2} <R $
즉, $ z $는 $ x $와 x의 반경 내부에 들어와 있기 때문에 $ f_{o}\left(x\right) \leq f_{o}(z)$가 성립해야 합니다. 하지만 convex optimization 같은 경우는 목적함수가 convex function이기 때문에
- $ z=\left( 1-\theta \right) x+\theta y,\, \theta \in [0,1]$
- $ f_{o}(z)\leq \left( 1-\theta \right) f_{o}(x)+\theta f_{o} (y)\leq f_{o}(x),\, \theta \in [0,1]$
하지만 이는 $ f_{o}\left(x\right) \leq f_{o}(z)$ 에 위배되는 상황 입니다.
따라서 우리가 가정했던 $ x $를 제외한 다른 global optimal이 있다 라는 가정은 참이 아닌 것으로 증명이 됩니다.
고로 convex optimization에서 $ x $가 locally optimal이라면 그와 동시에 global optimal이라는 것이 증명되었습니다.
Optimality criterion
다음으로는 목적함수 $ f_{o}$가 미분 가능한 함수일 때 optimal point를 결정짓는 optimally criterion 하나를 소개하도록 하겠습니다.
우선 $ f_{o}$가 convex function이기 때문에 first order condition을 만족하게 됩니다.
- $ f_{o}(x)+\nabla f_{o}(x)^{\rm{T}}\left(y-x\right)\leq f_{o}\left(y\right)$
여기서 만약에 $ x $가 optimal solution이라 가정한다면 $ f_{o}(x)\leq f_{o}\left(y\right) $이 항상 성립합니다.
그런데 이게 항상 성립되기 위해서는 $\nabla f_{o}(x)^{\rm{T}}(y-x) \geq 0$이 만족해야 합니다.
- $\nabla f_{o}(x)^{\rm{T}}(y-x) \geq 0$
따라서 해당 조건이 성립한다면 $ x $는 optimal point입니다.
기하학적으로 간단하게 설명하면 $(y-x)$ 벡터와 $x$ 의 그래디언트의 코사인이 항상 양의 값을 가진다는 의미로 사이각이 예각이라는 뜻입니다.
여기서 다루는 Optimality Criterion 말고도 뒤에서 몇 가지 중요한 Optimality Condition들을 다룰 예정인데 그건 그때 가서 또 자세히 얘기해보도록 하겠습니다.
Proof)
우선 여기서 다룬 이 optimality criterion이 성립하는지 증명을 한번 같이 해보도록 하겠습니다.
우리가 증명하고 싶은 것은 $ x $가 optimal point일 때 $ f_{o}(x)\leq f_{o}\left(y\right) $이 성립하는지를 알고 싶은 것이고
반대로 $ f_{o}(x)\leq f_{o}\left(y\right) $이 성립할 때 $ x $가 optimal point 인지 알아보는 것입니다.
$ x $가 optimal point일 때 $ f_{o}(x)\leq f_{o}\left(y\right) $이 성립하는 것은 위에서 살펴봤고,
이제 $f_{o}(x)\leq f_{o}\left(y\right) $이 성립할 때 $ x $가 optimal point 인지 알아보겠습니다.
우선 $ x $가 optimal point 일 때 $\nabla f_{o}(x)^{\rm{T}}(y-x) < 0$이 성립한다고 가정해보도록 하겠습니다.
이번에도 반대의 상황을 가정하고 이것이 모순됨을 보이는 것이 증명의 방향입니다.
- $\nabla f_{o}(x)^{\rm{T}}(y-x) < 0$
그러고 나서 $ z(t)=ty+\left(1-t\right) x $, line segment를 정의합니다.
다음으로 $ f(z(t))=f(ty+\left( 1-t\right) x)$ 에서 $ t=0 $ 일 때의 미분을 구해보겠습니다. $ g(0)=x $이기 때문에 $ x $ 근방에서의 증감을 확인하기 위함입니다.
- $\frac {d}{dt} f_{o}(z(t))|_{t=0}=\nabla f_{o}(x)^{\rm{T}}(y-x)<0 $
자 $ f_{o}$는 $ x $ 근방에서 감소 함수라는 뜻입니다.
하지만 $ x $ 근방의 아주 작은 양의 값 $ t $에 대해서도 $ x $가 optimal point이기 때문에
- $ f_{o}(x)<f_{o}(z(t))$
이 성립해야 하지만 이는 $ x $ 근방에서 감소 함수라는 것에 대해서는 모순이죠.
즉, 처음에 했던 가정 $\nabla f_{o}(x)^{\rm{T}}(y-x) < 0$이 모순이고
원래 $\nabla f_{o}(x)^{\rm{T}}(y-x) \geq 0$이 만족한다는 것을 우리는 알 수 있습니다.
여기까지 증명한 것은 convex optimization이 inequality constraints와 equality constraints가 존재할 때 optimality criterion이었습니다.
만약에 convex optimization이 unconstrained problem이라면 굉장히 쉽게 풀 수 있습니다.
$\nabla f_{o}(x)=0 $ 지점이 global optimal입니다. 증명은 간단하니 직접 해보시길 바랍니다.
Conclusion
이상으로 convex optimization이 무엇인지 간단하게 소개하였습니다.
앞으로 다룰 내용들은 convex optimization의 예시와 이를 풀 수 있는 몇가지 알고리즘들에 대해서 알아볼 예정입니다.
감사합니다.
'Math > Convex Optimization' 카테고리의 다른 글
| Optimization Theory (Gradient Descent - Convergence Analysis) (2) | 2022.09.08 |
|---|---|
| Optimization Theory (Unconstrained Optimization) (0) | 2022.09.08 |
| Optimization Theory (Convex Functions Ⅱ) (2) | 2022.04.23 |
| Optimization Theory (Convex Functions Ⅰ) (1) | 2022.04.23 |
| Optimization Theory (Convex Sets) (0) | 2022.04.23 |



