Intro
1. Unconstrained Optimization
$\min f(x)$
$f:\mathbb{R}^{n}\rightarrow \mathbb{R}$가 convex function이고 두 번 연속 미분 가능할 때 optimal point $x^{\star }$에 대한 필요충분조건은 다음과 같습니다.
$\nabla f(x^{\star })=0$
주의해야 할 것은 constraint가 없는 상황일 때, 필요충분조건이라는 것입니다.
직관적으로 생각해보면 볼록 함수는 global minimum이 전체 domain에 대해서 유일하게 존재하기 때문에
$\nabla f(x^{\star })=0$인 지점은 local minimum이자 global minimum이 되는 것이지요.
그래서 사실 unconstrained 상황에서의 convex optimization은 쉬운 축에 속합니다.
Gradient를 계산하고 0이 되는 지점만 찾아주면 되기 때문이죠.
결국 목적함수의 도함수를 구하고 도함수의 근(root)를 찾는 것이 목적이라 보면 되겠습니다.
어떤 함수의 근을 찾는 방법은 크게 두 가지로 분류할 수 있습니다.
Analytical solution과 Numerical solution이라 볼 수 있죠.
Analytical solution은 쉽게 말하면 정확한 해를 찾는 것입니다. 한치의 오차도 없는 그러한 solution이라 생각할 수 있겠네요.
Numerical solution은 정확하지는 않지만 상당히 유사한 해를 찾는 것입니다.
우선 analytic 하게 해를 찾았을 때의 예시를 하나 보도록 하겠습니다.
간단하게 Least-Square 예시를 들어보도록 하겠습니다.
- $\min \parallel Ax-b\parallel^{2}_{2} $
- $\parallel Ax-b\parallel^{2}_{2} =(Ax-b)^{\rm{T}}(Ax-b)$
- $(Ax-b)^{\rm{T}}(Ax-b)=x^{\rm{T}}(A^{\rm{T}}A)x-2(A^{\rm{T}}b)^{\rm{T}}x+b^{\rm{T}}b$
- $f_{o}(x)=x^{\rm{T}}(A^{\rm{T}}A)x-2(A^{\rm{T}}b)^{\rm{T}}x+b^{\rm{T}}b$
- $\nabla_{x} f_{o}(x)=(A^{\rm{T}}A+AA^{\rm{T}})x-2(A^{\rm{T}}b)^{\rm{T}}=0$
- $A^{\rm{T}}Ax=A^{\rm{T}}b \rightarrow x=\left( A^{\rm{T}}A\right)^{-1} A^{\rm{T}}b$
중요한 것은 $ \left( A^{\rm{T}}A\right)^{-1} $이 존재해야 하는 것이고, 모든 column이 선형 독립이라면 가능합니다. 역행렬이 존재하지 않는다면 특이값 분해를 통해 유사역행렬을 계산해야 합니다.
이처럼 해석적인 접근은 오차가 없기 때문에 모든 해를 analytic 하게 구하는 것이 좋겠지만 쉽지 않을 때가 있죠.
예를 들면 4차 다항식을 넘어가는 고차 다항식은 analytic 하게 해를 구하기가 쉽지 않습니다.
또한 목적함수가 다항함수가 아닌 초월함수로 섞여 있는 경우는 더욱 힘들겠죠.
그래서 수치적으로 $\nabla f(x^{\star })=0$ 에 해당하는 근(root)을 찾는 방법이 필요합니다.
오늘 포스팅에서는 3가지 방법에 대해서 알아볼 예정입니다.
2. Numerical Approach
Bisection Method
가장 먼저 이분법(bisection method)이라 불리는 방법론입니다.
Convex optimization에서는 $\nabla f(x^{\star })=0$에 해당하는 근(root)을 찾아야 하는데 여기에 bisection method를 활용할 수 있습니다.
정확히 이분 탐색(Binary Search)과 동일합니다. 초기에 두 포인트를 지정하고 탐색 범위를 절반씩 줄여나가는 방법이라 볼 수 있습니다.
두 개의 initial point를 $x_{l}$ , $x_{u}$라고 했을 때 일단 다음을 만족해야 합니다.
- $f(x_{l})f(x_{u})<0$
두 포인트에 대응되는 치역의 부호가 반대여야 한다는 것입니다. 중간값 정리를 활용했다고 볼 수 있습니다.
함수가 연속함수이고 $f(x_{l})f(x_{u})<0$를 만족한다면 $x_{l}$과 $x_{u}$ 사이에 $f(x)=0$을 만족하는 $x$가 반드시 있다는 것이죠.
자 이제 중간값 정리를 통해 $x_{l}$과 $x_{u}$ 사이에 근(root)가 있다는 것은 보장을 하였으니 그 위치를 찾아야겠습니다.
가장 쉬운 방법은 탐색 범위인 $x_{u}-x_{l}$를 절반씩 줄여나가는 방법입니다.

알고리즘은 간단합니다. $x_{l}$과 $x_{u}$ 사이에 존재하는 중앙점($x_{r}=\frac{x_{l}+x_{r}}{2}$)을 계산합니다.
그리고 영역을 조사합니다. 만약 $f(x_{l})f(x_{r})<0$ 라면 우리의 탐색 범위는 $x_{l}$ 부터 $x_{r}$까지가 됩니다.
반대로 $f(x_{r})f(x_{u})<0$ 라면 우리의 탐색 범위는 $x_{r}$ 부터 $x_{u}$까지가 됩니다.
그런데 종료 조건을 보면 $f(x_{l})f(x_{u})=0$ 이렇게 되어있습니다.
하지만 실제로 완전히 0이 되는 지점을 찾을 수 없는 경우도 있기 때문에 $|x_{l}-x_{u}|<\epsilon $ 이렇게 두 구간이 매우 작은 임의의 값보다 작을 때 종료시키는 조건을 만들어서 알고리즘을 종료시키기도 합니다.
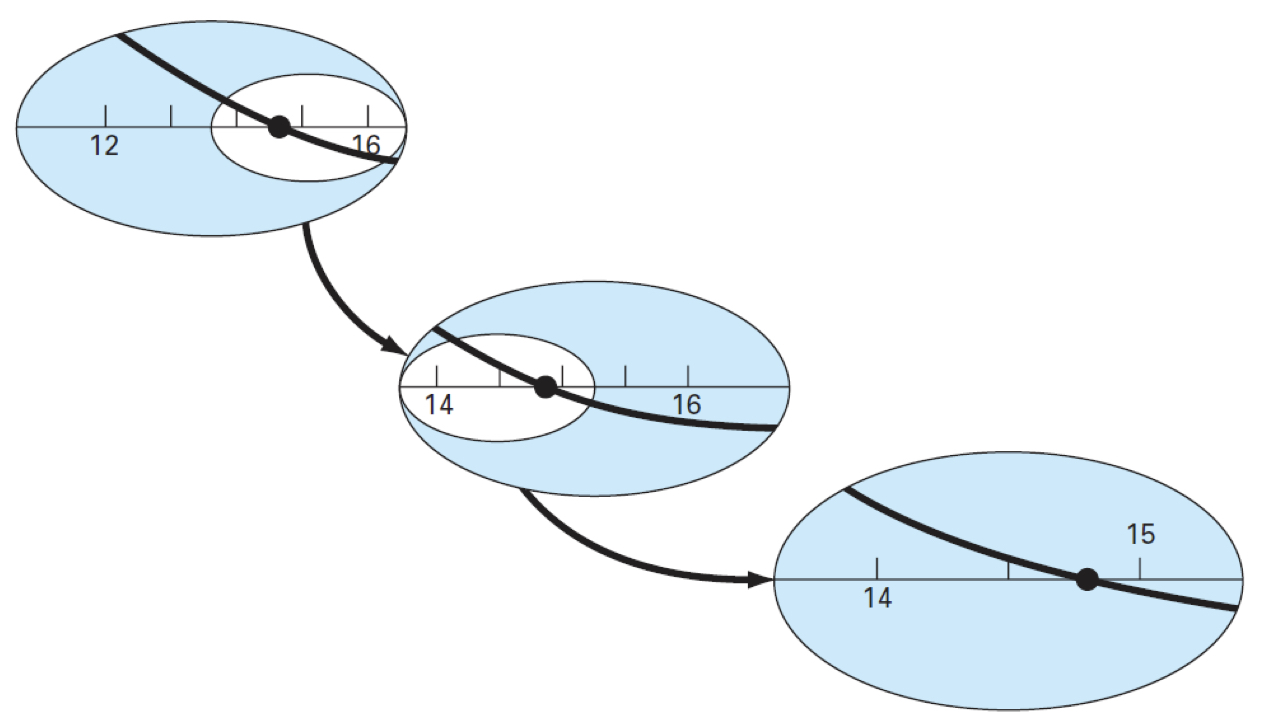
탐색 구간이 점점 절반씩 되는 모습을 그림을 통해 확인할 수 있습니다.
이분법은 간편하기도 하고 무조건 수렴 포인트를 찾을 수 있어 근(root)을 찾을 때 많이 사용되는 수치해석적 접근입니다.
매트랩을 활용해보셨다면 알겠지만 매트랩의 roots라는 함수 역시 bisection method에 그 뿌리를 두고 있습니다.
Newton's Method
유명하신 뉴턴 선생님의 방법론입니다.
핵심은 어느 한 포인트에서 일차 테일러 근사를 통해 탐색 범위를 줄여나가는 방법입니다.
아래의 그림을 보면 이해하기 쉬울 것 같습니다.
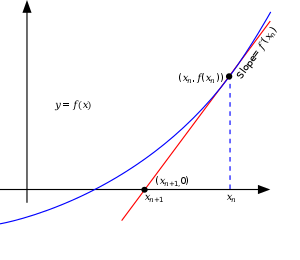
$x_{n}$이라는 포인트에서 시작을 한다고 했을 때 $x_{n}$ 포인트에 해당하는 일차 테일러 근사(접선)를 계산합니다.
직선의 기울기 공식을 이용하면 다음의 관계식을 얻을 수 있습니다.
- $\frac{f(x_{n})}{x_{n}-x_{n+1}} =f^{\prime }(x_{n})$
그리고 이 관계식을 정리하면
- $x_{n+1}=x_{n}-\frac{f(x_{n})}{f^{\prime }(x_{n})}$
이렇게 정리가 되는데 결국 새롭게 업데이트되는 $x_{n+1}$를 따라가다 보면 우리가 찾고자 하는 근(root)에 도달할 수 있는 방법론입니다.
그리고 종료 조건은 $x_{n+1}=x_{n}$이 되거나 아니면 $|x_{n+1}-x_{n}|<\epsilon $ 이렇게 설정하기도 합니다.
훌륭한 수치해석적 방법이지만 그렇다고 해서 무조건 해를 찾을 수 있다는 보장은 또 없습니다.
해가 존재하는데도 Newton-Raphson 방법은 발산할 수 있습니다. 또한 함수가 미분 가능해야 한다는 제약식이 붙기도 하고요.
또한 한 가지 문제점은 우리가 찾는 것은 도함수의 근을 찾는 것이기 때문에 뉴턴 방법을 사용하려면 2차 미분인 hessian을 계산해야 합니다.
이 hessian을 계산하는 Cost가 크기 때문에 일반적으로는 많이 사용되지 않는 방법론입니다.
Gradient Descent
경사 하강법이라고 불리는 이 알고리즘은 특히나 요즘 딥러닝/머신러닝이 유명해지면서 같이 많이 알려진 알고리즘입니다.
Unconstrained convex optimization에서 optimal point는 $\nabla f(x^{\star })=0$ 를 만족한다고 했습니다.
함수를 minimize 하는 입장에서는 함수가 줄어드는 방향으로 가다 보면 언젠가는 어떠한 minima에 수렴할 수 있고 그 부근에서 gradient가 0으로 수렴하는 지점을 찾을 수 있습니다.
그렇다면 함수가 줄어드는 방향은 어떻게 찾을까요?
여기서는 경사 하강법(Gradient Descent)이라는 방법이 등장하게 됩니다.
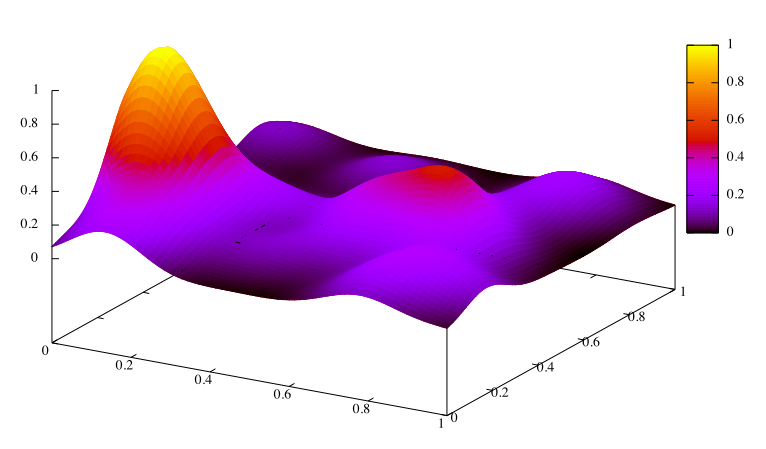
다변수 함수 입장에서는 어느 한 Point에서의 미분(방향 도함수)은 여러 개의 방향으로 정의가 됩니다.
즉 무한개의 방향벡터가 정의되는 데 우리는 그중에서 함수가 줄어드는 방향을 찾고 싶습니다.
기왕이면 가장 빠르게 줄어드는 방향이 좋겠죠?
그래서 그래디언트(Gradient)라는 것이 등장합니다.
그래디언트는 다변수 함수의 최대 증가 방향을 나타내는 벡터로 가장 가파르게 증가하는 방향이라 이해하면 됩니다.
가장 가파르게 증가하는 방향의 반대 방향은 어떻게 해석할 수 있을까요?
가장 가파르게 감소하는 방향이겠죠?
즉 가장 빠르게 줄어드는 방향으로 우리의 최적화 방향이라 볼 수 있습니다.
- Gradient : $\nabla L(w_{1},w_{2},\ldots ,w_{n})=\left( \frac{\partial L}{\partial w_{1}} ,\frac{\partial L}{\partial w_{2}} ,\ldots ,\frac{\partial L}{\partial w_{n}} \right) $
Gradient는 각 함수의 성분을 구성하는 독립변수에 대해 그 각각의 방향의 편미분으로 구성된 벡터로 정의가 됩니다.
- $\overrightarrow{w} =\overrightarrow{w} -\eta \times \nabla L(\overrightarrow{w} )$
즉 우리의 parameter인 $\overrightarrow{w}$를 gradient의 반대 방향으로 어떠한 step size 만큼 업데이트해주는 방식이 Gradient Descent 기반의 최적화 방식입니다.
결국 어떠한 최소 지점을 찾고 싶은데 우선 가장 가파르게 감소하는 방향으로만 step을 밟아나가다 보면 어떠한 지점에 수렴할 수 있지 않을까?라는 게 경사 하강법(Gradient Descent)의 아이디어입니다.
Vanilla gradient descent는 convex optimization 같은 경우에는 무조건 수렴할 수 있습니다.
다음 포스팅에서 간단한 증명도 할 예정입니다.
하지만 non convex optimization 상황에서는 당연히 수렴을 보장할 수 없습니다.
Convex optimization을 이제 막 공부하는 입장에서 non convex의 상황까지 다루기는 아직 이른 것 같으니 저의 실력이 충분히 올라왔을 때 조금 더 general 한 상황에서의 optimization도 언젠가 포스팅하도록 하겠습니다.
정리하자면 unconstrained 상황에서의 convex optimization은 $\nabla f(x^{\star })=0$ 지점만 찾으면 된다고 설명했습니다. 도함수가 0이 되는 근을 찾는 것이 핵심이죠.
Conclusion
다음 포스팅에서는 Convex Optimization이고 목적함수가 미분 가능하며 립시츠 연속성을 가지고 있을 때 Gradient Descent 방식이 무조건 수렴할 수 있음을 증명해보도록 하겠습니다.
감사합니다.
'Math > Convex Optimization' 카테고리의 다른 글
| Optimization Theory (Duality) (3) | 2024.11.12 |
|---|---|
| Optimization Theory (Gradient Descent - Convergence Analysis) (2) | 2022.09.08 |
| Optimization Theory (Convex Optimization Problems) (0) | 2022.05.03 |
| Optimization Theory (Convex Functions Ⅱ) (2) | 2022.04.23 |
| Optimization Theory (Convex Functions Ⅰ) (1) | 2022.04.23 |



