Intro
이번 포스팅에서는 최적화 이론에서 굉장히 중요하게 다뤄지는 쌍대성(duality)에 대해서 알아보도록 하겠습니다. 최적화 문제에서 쌍대성(duality)은 주어진 원 문제(primal problem)와 이 문제에 대응하는 쌍대 문제(dual problem) 사이의 관계를 의미합니다
쌍대 문제를 푸는 것은 복잡한 원 문제를 더 쉽게 풀기 위해 사용되며, 특히 비선형 최적화나 제약 조건이 포함된 문제에서 유용하게 쓰입니다.
사실 대부분의 최적화 문제는 non convex problem 일 것이고 정확한 솔루션을 찾는 것이 어려운 경우가 굉장히 많습니다. 그럴 때 이 쌍대 문제 (dual problem)이 우리가 찾고자 하는 global solution의 bound를 제공하기도 하고, 특정한 조건에서는 global solution 임을 보장할 수도 있습니다. 즉, 자주 사용되는 테크닉이라는 의미입니다.
1. Duality
Duality
우선, 다시 한번 최적화 문제의 정의를 살펴보는 것으로 시작하겠습니다.
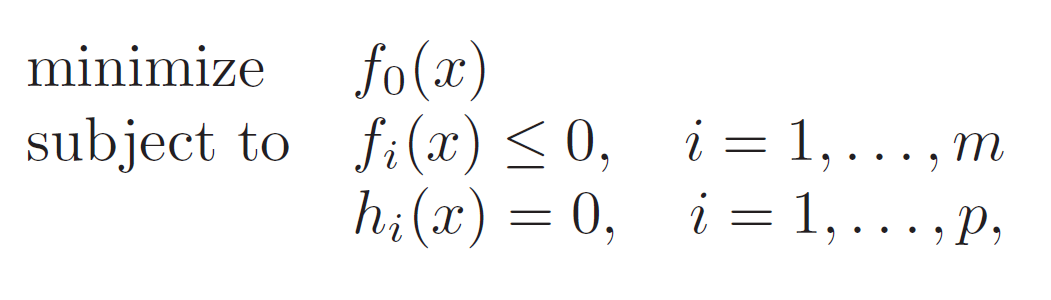
목적 변수 $x \in \mathbb{R}^{n}$가 있을 때, 일단 최적화 문제가 convex optimization이 아니라 가정해 보겠습니다.
목적함수를 최소화하는 $ x^{\star} $를 찾는 것이 목표인데, 이 $ x $는 constraints를 만족해야 한다고 했습니다.
- $ f_{i}(x)\leq 0, i=1,\ldots , m $는 inequality constraints라고 정의합니다.
- $ h_{i}(x)=0, i=1,\ldots , p $는 equality constraints라고 정의됩니다.
$ \mathcal{D}=\bigcap^{m}_{i=1} \text{dom}(f_{i}) \cap \bigcap^{p}_{i=1} \text{dom}(h_{i})$이 feasible set이 되겠네요.
그리고 이 feasibile set이 optimization problem의 정의역이 되는 것입니다. 여기서는 feasible set이 nonempty set이라는 가정을 하나 두겠습니다.
그리고 우리의 목적은 optimization problem에 해당하는 최적의 솔루션(optimal value)을 찾는 것입니다.
- $ p^{\ast }=\inf\left\{f_{o}\left(x\right) | f_{i}\left(x\right)\leq 0, i=1,\ldots, m, h_{i}\left(x\right)=0, i=1,\ldots , p\right\}$
그런데 사실 제약 조건이 있고, convex optimization이 아닌 문제들을 바로 해결하는 것은 난이도가 높습니다. 해결할 수 없는 문제도 많고요.
그래서 duality라는 것이 등장합니다.
짤막하게 역사를 소개하면, 처음에는 물리학의 입자 운동 원리를 설명하기 위해 등장했다가 미적분이 발전하고 변분법, 최적화 이론이 발전하는 과정에서 자연스럽게 등장한 이론으로 제약 조건이 있는 문제를 효율적으로 분석하고 푸는 방법을 제공하기 위해 발전해 왔습니다.
최적화 이론에서의 쌍대성(duality)은 임의의 최적화 문제를 바라볼 때, 원초문제(primal problem)와 쌍대문제(the dual problem) 사이의 관계를 의미합니다.
여기서 원초문제(primal problem)는 원래의 최적화 문제 그대로를 의미합니다.
쌍대 문제는 뒤에서 바로 소개하겠지만 원초문제의 Bound를 제공해주는 문제 입니다.
최적화 관점에서 쌍대문제의 상한은 원초문제의 하한이 됩니다.
왜 이런 관계를 가지는 지는 조금 뒤에서 다시 설명하는 것으로 하겠습니다. 쌍대 문제를 그럼 어떻게 정의할까요?
이를 설명하게 위해 이제 가장 보편적으로 사용되는 라그랑주 승수법에 대해서 설명해 보도록 하겠습니다.
The Lagrangian

위의 정의는 Lagrangian ($ L : \mathbb{R}^{n} \times \mathbb{R}^{m} \times \mathbb{R}^{p} \rightarrow \mathbb{R}$) 이라 합니다.
$ L(x,\lambda,\nu)$ 는 결국 목적 함수와 제약식들의 선형 결합의 형태로 정의되고 있고 여기서 $ \lambda,\nu $를 우리는 라그랑주 승수 (Lagrange multiplier) 라고 정의합니다. 정확히는 라그랑주 승수 벡터이죠. 듀얼 벡터라고도 정의합니다. 결국 라그랑주 함수는 이제 $ x,\lambda,\nu$의 함수라고 보시면 됩니다.
직관적으로 목적 함수 $f_{o}(x)$를 최적화할 때,
- 제약 조건을 모두 따져가면서 최적화를 하는 것
- 제약 조건을 목적 함수에 선형 결합 형태로 합치는 것
둘 중 어느 시나리오가 더 풀기 쉬울까요? 제약 조건을 그냥 목적 함수에 더해버리는 방식이 최적화 난이도는 낮아지겠죠?
하지만 제약조건을 직접적으로 만족시키는 것은 아니기 때문에 원초 문제 (primal problem)의 직접적인 해는 아닐 것입니다. 그럼에도 어느 정도 bound를 제공한다는 관점에서는 꽤나 의미 있는 접근입니다. 이렇게 라그랑주 승수를 이용하여 문제를 푸는 것은 라그랑주 쌍대 문제 (Lagrangian dual problem)라고 정의합니다.
쌍대 문제를 푸는 가장 큰 이유는 원래의 원초 문제를 더 쉽게 해결하거나 분석 (효율적 계산, 해석적 통찰, 분산 최적화) 할 수 있도록 하기 위한 대안이라 생각하시면 될 거 같습니다.
쌍대 문제를 정의하기 위해서 라그랑주 승수 말고도 다양한 방법이 있긴 합니다.
따라서 쌍대 문제 = 라그랑주 승수법 이렇게 이해하시면 곤란합니다.
저도 자세히는 공부해보지 않아 위키피디아 링크만 정리해 둡니다. 관심 있으시면 한번 찾아보시는 것도 좋을 거 같습니다. 우선 이번 포스팅에서는 라그랑주 승수법에 기반한 쌍대 문제에 대해서만 다루도록 하겠습니다.
2. The Lagrange dual problem
The Lagrange dual function
우선 정의부터 시작하도록 하겠습니다. 라그랑주 듀얼 함수 (Lagrange dual function) 은 아래와 같이 정의합니다.
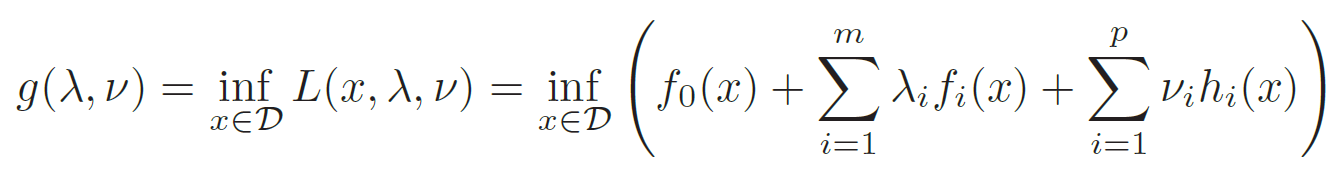
$\lambda,\nu$를 고정된 상수로 취급하고 $L(x,\lambda,\nu)$를 $x$ 에 대해서만 최적화 시켰다고 보시면 됩니다. 그렇게 optimal 한 $x^{\star}$ 를 찾으면 $x$에 대해서 고정할 수 있겠네요.
다시 정리해서 라그랑주 쌍대 함수 $g(\lambda, \nu )$ 은 라그랑주 승수인 $\lambda,\nu$ 에 대한 목적함수라고 보시면 되겠습니다.
이때 $\lambda \succeq 0 $는 만족해야 합니다. (부등식 제약조건의 부등호 방향을 유지하기 위해)
이렇게 정의된 쌍대 함수는 원초 문제에 대해서 lower bound를 제공합니다. 원초문제에서 optimal value를 $p^{\star}$ 라 정의할 때,
$g(\lambda, \nu ) \leq p^{\star}$
를 항상 만족합니다.
왜 항상 lower bound를 제공할까요? 이를 이해하는 것은 매우 중요합니다. 따라서 간단하게 증명 같이 해보도록 하겠습니다.
우선, $\tilde{x}$를 원초문제에 대한 임의의 feasible point라 가정하겠습니다. 이 feasible point를 contraint 들에 대입하면
$\sum_{i=1}^{m}\lambda_{i}f_{i}(\tilde{x})+\sum_{i=1}^{p}\nu_{i}h_{i}(\tilde{x})\leq 0$
를 만족합니다. 이는 단순히 equality, inequality 조건에 대입한 결과 입니다.
여기서 양변에 $f_{o}(\tilde{x})$를 더해보겠습니다.
$ L(\tilde{x} ,\lambda,\nu) = f_{o}(\tilde{x}) + \sum_{i=1}^{m}\lambda_{i}f_{i}(\tilde{x})+\sum_{i=1}^{p}\nu_{i}h_{i}(\tilde{x})\leq f_{o}(\tilde{x}) $
그리고 당연하게도 dual function은 $x$에 대해서는 infimum 이기 때문에 다음이 성립합니다.
$g(\lambda,\nu)=\inf_{x \in \mathcal{D}} L(x,\lambda,\nu) \leq L(\tilde{x} ,\lambda,\nu) \leq f_{o}(\tilde{x}) $
정리하고 보니 $g(\lambda,\nu) \leq f_{o}(\tilde{x}) $이 성립합니다.
즉, $g(\lambda,\nu)$는 어떠한 feasible point 에 대해서도 lower bound를 제공하기 때문에 $g(\lambda, \nu ) \leq p^{\star}$도 참이 됩니다.
자 그렇다면 다시 한번 dual function에 대해서 정리해 보겠습니다.
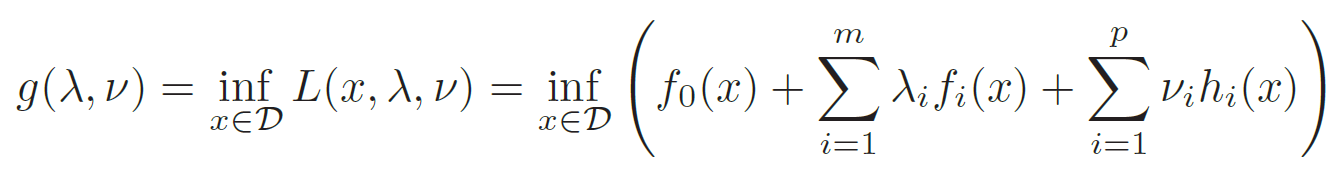
$g(\lambda, \nu )$ 은 라그랑주 승수인 $\lambda,\nu$ 에 대한 목적함수입니다. 그런데 동시에 concave function입니다.
이는 $g(\lambda, \nu )$가 ($\lambda,\nu$)에 대해서 affine 함수의 pointwise infimum 이기 때문입니다.
제가 convexity를 보존하는 연산에 대해서는 지난 포스팅에서 다룬 적이 있습니다.
간단하게 말하면 affine 함수의 pointwise maximum이라면 convex, infimum이라면 concave가 되는 것이죠.
즉, dual function은 concave function입니다.
$g(\lambda,\nu) \leq g^{\star}(\lambda,\nu) \leq f_{o}(\tilde{x}) $
그렇다면 우리는 가능한 dual function 중에서 가장 큰 값 $ g^{\star}(\lambda,\nu) $ 을 찾아야 가장 근접한 lower bound를 제공할 수 있습니다.
예를 들어 남자의 평균키는 175cm라 가정했을 때 dual problem이 제공하는 bound가 "한국 남자의 평균키는 50cm 이상입니다."라고 해버리면 의미가 없기 때문이죠.
Dual function은 concave function이고 concave function의 최댓값을 찾는 문제 역시 convex optimization problem입니다.
이것이 Lagrange duality가 제공하는 강력함입니다. 원초문제가 convex problem이 아니어도, 쌍대문제는 convex problem으로 상회해서 풀 수 있습니다.
그렇다면 이제 쌍대문제를 정의해 보겠습니다.
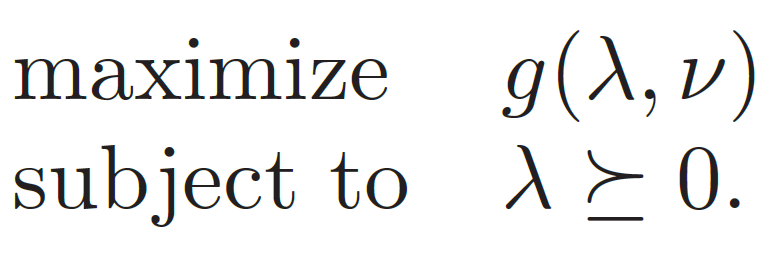
쌍대문제는 concave 함수의 최대화 문제입니다. 즉, Convex optimization 이므로 무조건 해를 찾을 수 있죠. 쌍대문제에서의 optimal value를 $d^{\star}$라 하고 원초문제에서의 optimal value를 $p^{\star}$라 정의하겠습니다.
$ d^{\star} \leq p^{\star} $
쌍대문제를 convex optimization을 통해 해결했다고 하더라도 일반적으로는 gap이 존재합니다.
Weak duality
이렇게 $d^{\star} \leq p^{\star}$, gap이 있는 상황을 weak duality라 정의합니다. 그리고 대다수의 문제들이 weak duality 상황이라 보시면 됩니다. 그래서 굉장히 작은 gap을 두고 $ \left\|p^{\star} - d^{\star} \right\| < \epsilon $ 라는 것을 증명할 수 있으면 $ d^{\star} $를 sub optimal 이라고도 정의합니다.
Strong duality
하지만 특정한 조건을 만족한다면 $d^{\star} = p^{\star}$, gap 없는 상황도 존재합니다.
1. 원초문제가 convex optimization 이면서
2. Constraints qualifications (Regularity condition)를 만족해야 합니다.
우선 constaints qualification 들은 다양하게 있지만 convex optimization의 경우 slater condition이 자주 등장하는 것 같습니다. 이번 포스팅에서 다루지는 않고 다음 optimality condition을 다룰 때 더 자세히 설명드리도록 하겠습니다.
Conclusion
이번 포스팅에서는 쌍대성 (Duality)에 대해서 알아보았습니다.
최적화 이론에서 굉장히 자주 사용되는 테크닉인데 개념적으로 먼저 정리해 보았습니다.
다음 포스팅에서는 duality를 활용하여 몇 가지 최적화 문제를 풀어보도록 하겠습니다.
감사합니다.
'Math > Convex Optimization' 카테고리의 다른 글
| Optimization Theory (Gradient Descent - Convergence Analysis) (2) | 2022.09.08 |
|---|---|
| Optimization Theory (Unconstrained Optimization) (0) | 2022.09.08 |
| Optimization Theory (Convex Optimization Problems) (0) | 2022.05.03 |
| Optimization Theory (Convex Functions Ⅱ) (2) | 2022.04.23 |
| Optimization Theory (Convex Functions Ⅰ) (1) | 2022.04.23 |



