Intro
Optimization theory 포스팅에서는 Stephen Boyd 교수님의 Convex Optimization 을 정리합니다. 사실 저는 ML 보다는 좀 더 응용에 가까운 딥러닝 연구에 관심이 있지만, 학부때 수업을 듣기도 했고, 정리 해두면 언젠가 도움이 될 거 같아 블로그에 정리합니다.
수학 전공은 아니라, 포스팅 내용에 오타나 오류가 있을 수 있습니다. 댓글로 코멘트 주시면 감사드리겠습니다.
Optimization Problem
일단 최적화 이론 자체는 응용분야가 상당히 많습니다. 신호처리나 제어공학, 통신 시스템 등 다양한 분야에서 사용이 될 수 있지만, 제가 관심을 가지는 머신러닝/딥러닝에서도 최적화는 많이 활용이 됩니다.
애초에 neural network의 학습 자체가 최적화 문제이기 때문이죠. 우리가 target으로 하는 down stream task 목적 함수의 최대, 최소 지점을 잘 찾아야 하는 최적화 문제 입니다. 저는 경사 하강법이라는 알고리즘이 처음에는 신경망 학습을 위해 고안된 줄 알았는데, 나중에 알고보니 수치적 최적화 방법중 하나인 것을 알게 되었네요.
우선 이 포스팅에서 집중적으로 다루는 문제는 Convex Optimization입니다.

우리가 일반적으로 머신러닝/딥러닝에서 마주하게 되는 최적화 문제는 non convex 문제에 해당합니다. 신경망 내부에는 비 선형적인 연산들이 필연적으로 존재하고 그로 인해 만들어지는 loss landscape는 convexity의 성질을 잃게 됩니다.
그럼에도 불구하고 convex optimization을 배워야 하는 이유는 (1) 사실 가장 기본이 되는 구조이기도 하며, (2) 어떤 상황에서는 non convex problem을 convex problem으로 근사할 수 있기 때문입니다. (Relaxation)
Convexity가 보장되면 최적화 관점에서 무엇이 좋을까요?
Local minima = global minima라는 것을 무조건 보장할 수 있기 때문입니다. 이것에 대한 증명은 이번 글이 아니라 추후에 작성되는 글에서 다뤄질 것 같습니다. 아무튼 최적화 입장에서 convexity가 보장되면 문제를 쉽게 풀 수 있기 때문에 convex optimization이 최적화 이론에서 중요하게 다뤄지는 것 같습니다.
그럼 이제 본격적으로 시작해 보도록 하겠습니다. 이번 글에서 다룰 내용은 convex set에 대한 이야기로 최적화에 대한 내용은 아닙니다. 본격적인 최적화 이론을 공부하기 위한 준비 운동이라 보면 될 것 같네요.
Convex Sets
1. Affine and Convex Sets
Line과 Line Segment의 차이를 알아보면서 시작하겠습니다. Line은 두 Point를 지나면서 무한하게 펼쳐지는 직선입니다. Line Segment는 두 Point를 이어주는 선분이죠
- Line : $y=\theta x_{1}+(1-\theta )x_{2}, \; \theta \in \mathbb{R}$
- Line Segment : $y=\theta x_{1}+(1-\theta )x_{2},\;\theta \in [0,1]$
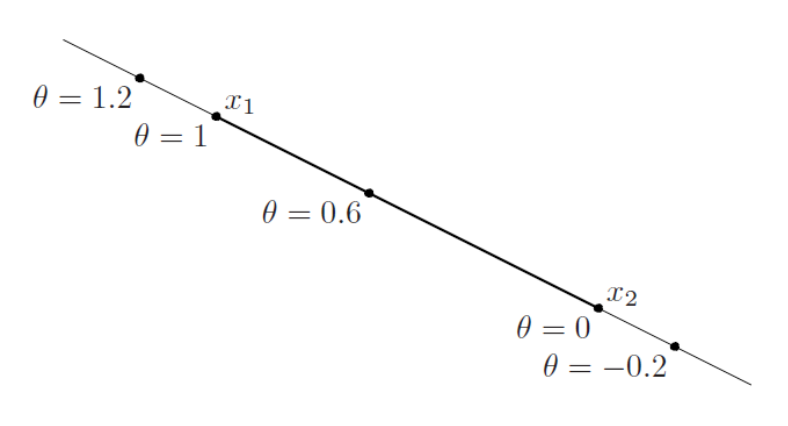
여기서 차이는 계수비 ($\theta$) 를 조정하면서 정의를 한다는 점이죠. 그리고 여기서부터 Affine Set과 Convex Set의 정의가 출발하게 됩니다.
Affine Sets
- 임의의 집합 $\mathbf{C}$가 있다고 가정할 때, 임의의 두 point 간 line 역시 집합 $\mathbf{C}$에 포함된다면 우리는 affine set이라 정의합니다.
- $\mathbf{C}=\left\{\theta_{1}x_{1}+\theta_{2}x_{2} \in \mathbf{C}\,|\, x_{1},x_{2} \in \mathbf{C}, \theta \in \mathbb{R} \right\}$
직선이나 평면 전체는 affine set이라 볼 수 있습니다. 하지만 원이나 타원, 삼각형 등은 affine 하다고 볼 수 없습니다. 직선이 affine 한 이유는 직선상 두 점을 어떻게 선택해도 만들어지는 line은 그 직선 자체가 되기 때문에 집합에 포함된다고 볼 수 있습니다. 또한 평면이 affine 한 이유는 평면 상 어느 두 점을 선택해도 만들어지는 그 line은 평면 내에 존재하기 때문입니다.
Affine set은 직선이나 평면처럼 두 점을 연결할 수 있고, 그 연결을 무한히 연장해도 여전히 그 집합 내에 머무르는 구조를 가진 집합입니다.
Affine combination
- $p = \theta_{1} x_{1}+\cdots +\theta_{k} x_{k}, \; \text{where} \sum^{k}_{i=1} \theta_{k} =1$를 affine combination이라 부릅니다.
Affine combination은 계수들의 합이 1이어야 하지만, 음수일 수도 있어 점들이 원래 점들의 선형 조합으로 확장된 공간을 포함할 수 있습니다. 즉, affine combination은 점들이 있는 평면이나 직선 등의 전체를 포함할 수 있습니다.
Affine hull
- $\text{aff}(C)=\{ \theta_{1} x_{1}+\ldots +\theta_{k} x_{k}\,|\,x_{1},\ldots x_{k}\in \mathbf{C},\theta_{1} +\ldots +\theta_{k} =1\}$
예를 들어 affine set이 아닌 그냥 임의의 집합 $\mathbf{C}$ 있다고 가정해 보겠습니다. 그 Set 안에 있는 모든 affine combination들의 합집합을 우리는 affine hull이라 부르고 set $\mathbf{C}$를 포함하는 가장 최소의 affine set입니다.
바로 뒤에서 convex hull이 무엇인지 알아볼 것인데, 그때 그림을 통해서 본다면 더욱 이해가 쉽기 때문에 여기서는 이 정도로 서술하고 다음으로 넘어가겠습니다.
Convex Sets
- 어떤 집합 $\mathbf{C}$가 있다고 가정할 때 임의의 두 point 간 line segment 역시 집합 $\mathbf{C}$에 포함된다면 convex set이라 정의합니다.
- $\mathbf{C}=\left\{\theta_{1}x_{1}+\theta_{2}x_{2} \in \mathbf{C}\,|\, x_{1},x_{2} \in \mathbf{C}, \theta \in [0,1] \right\}$
모든 affine Set은 convex set에 해당합니다. Affine set에서 두 point 간 line segment는 무조건 포함되기 때문입니다. 하지만 역은 성립하지 않습니다. 모든 convex set이 affine 한 것은 아니죠.
몇 가지 convex set과 non convex set을 그림으로 보도록 하겠습니다.
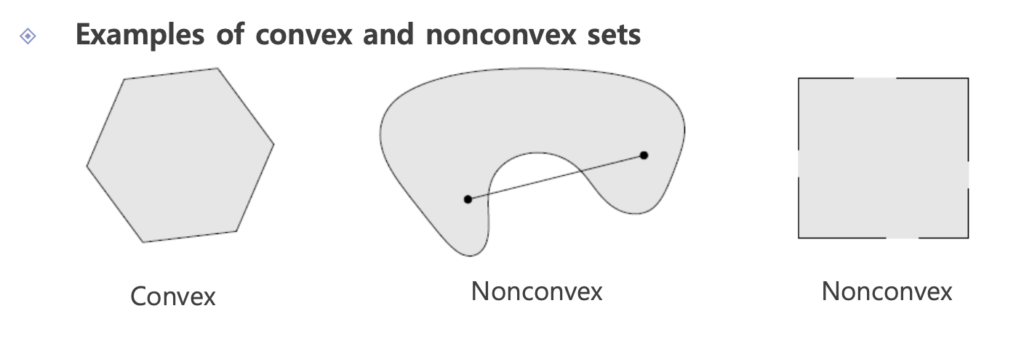
집합 안에 두 점을 임의로 잡아보고 두 점을 이어주는 선분을 그려봤을 때, 선분 전체가 집합 안에 포함된다면, convex set 아니면 non convex set입니다. 마지막 그림은 closed set이 아니기 때문에 line segment가 포함이 안 되는 부분이 있습니다. 따라서 non convex set 입니다.
Convex Combination
- $p = \theta_{1} x_{1}+\cdots +\theta_{k} x_{k}, \; \text{where} \sum^{k}_{i=1} \theta_{k} =1 , \theta_{i}\geq 0 $를 convex combination이라 부릅니다.
Affine combination과 조금 다른 점은 모든 계수들이 0 이상이 되어야 한다는 constraint가 추가로 붙는다는 점입니다.동일하게 convex set은 그 set 안에 있는 모든 point들 간의 convex combination을 포함하게 됩니다. Convex combination은 점들이 이루는 볼록 영역(예: 선분, 삼각형, 다면체 등) 내의 모든 점을 포함하게 만듭니다
Convex hull
- $\text{conv}(C)=\{ \theta_{1} x_{1}+\ldots +\theta_{k} x_{k}\,|\,x_{i}\in \mathbf{C},\theta_{i}\geq 0,i=1,\cdots,k, \theta_{1}+\ldots +\theta_{k} =1\}$
예를 들어 convex set이 아닌 그냥 임의의 집합 $\mathbf{C}$ 있다고 가정해 보겠습니다. 그 set 안에 있는 모든 convex combination들의 합집합을 우리는 convex hull이라 부르고 set $\mathbf{C}$를 포함하는 가장 최소의 convex set입니다.
Convex hull이 무엇인지 간단하게 그림을 통해서 알아보도록 하겠습니다.

왼쪽 그림을 먼저 보겠습니다. 집합 $\mathbf{C}$가 점들로 구성된 집합이라 가정했을 때, 집합 $\mathbf{C}$ 를 포함하는 가장 작은 convex Set은 왼쪽 오각형과 같습니다.
다음으로 오른쪽 그림을 보겠습니다. 집합 $\mathbf{C}$는 움푹 파인 형태를 가진 집합이라 했을 때, C를 포함하는 가장 작은 convex set은 오른쪽 도형과 같습니다.
Affine hull과 Convex hull은 집합을 확장하는 방법으로, 최적화 및 기하학에서 중요한 역할을 합니다. 각각의 개념은 집합의 구조를 이해하고, 그 집합이 포함할 수 있는 점들의 범위를 정의하는 데 사용됩니다.
Convex Cones
- 어떤 집합 $\mathbf{C}$가 있다고 가정할 때, 임의의 point를 가지고 양의 스칼라 실수 배를 취해도 여전히 그 집합에 포함된다면 cone이라 정의합니다. (Convex cone은 덧셈에도 닫혀있는 집합)
- $\mathbf{C}=\left\{\sum_{i=1}^{k}\theta_{i}x_{i}\,|\, \theta_{i}\geq 0 \,\text{, for all} \;i \right\}$
Convex set과 비교했을 때, 모든 계수들의 합이 1이어야 한다는 constraint가 사라졌다고 보면 됩니다. 따라서 이 집합은 무한한 영역을 가지게 됩니다. 원점으로 뻗어나가는 직선들이 만들어내는 영역이라 보면 됩니다. 그래서 항상 원점을 포함해야 합니다. 그림을 통해 알아보도록 하겠습니다.
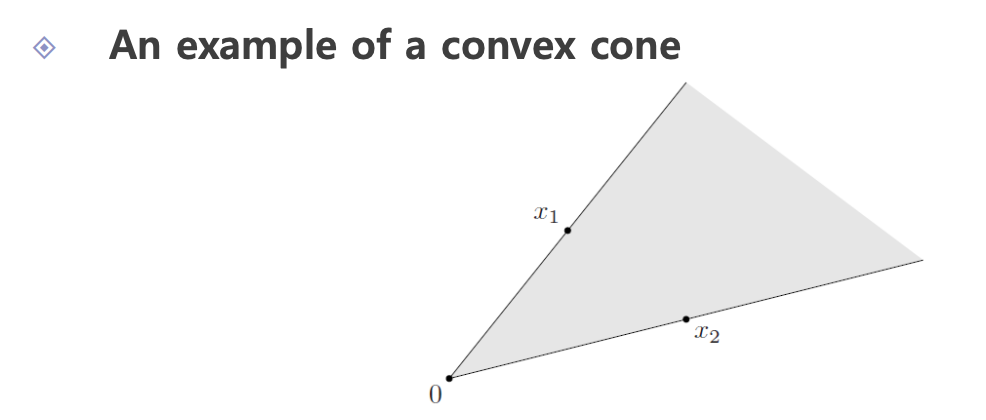
Convex cone은 원점에서 출발해 특정 벡터 방향으로 무한히 확장되는 볼록한 구조를 형성합니다. Convex cone은 더 높은 차원 공간에서도 특정 방향으로 뻗어 나가는 모든 점을 포함하며, 볼록성(즉, 두 점을 연결하는 선분이 항상 그 집합에 속하는 성질)을 유지합니다.
Convex cone은 원점에서 출발해 주어진 벡터들의 양의 선형 결합으로 무한히 확장되는 볼록한 집합을 의미합니다. 이 구조는 최적화 및 기하학 문제에서 핵심적인 역할을 합니다.
Conic Combination
- $p = \theta_{1} x_{1}+\cdots +\theta_{k} x_{k}, \text{where} \; \theta_{1},\cdots,\theta_{k} \geq 0$를 conic combination이라 부릅니다.
Convex combination과 다른 점은 모든 계수들의 합이 1이어야 한다는 constraint가 사라졌다는 점입니다. 동일하게 convex cone set은 그 set 안에 있는 모든 point들 간의 conic combination을 포함하게 됩니다. 그 set 안에서 어떤 point를 잡고 conic combination을 해도 그 set안에 포함될 수밖에 없다는 구조라 보면 됩니다.
Conic hull
- $\text{con}(\mathbf{C})=\{ \theta_{1} x_{1}+\ldots +\theta_{k} x_{k}\,|\,x_{i}\in \mathbf{C},\theta_{i}\geq 0,i=1,\cdots,k, \}$
예를 들어 conic set이 아닌 그냥 특정한 집합 $\mathbf{C}$ 있다고 가정해 보겠습니다. 그 set 안에 있는 모든 conic combination들의 합집합을 우리는 conic hull이라 부르고 set $\mathbf{C}$를 포함하는 가장 최소의 convex cone set입니다.
마지막으로 conic hull이 무엇인지 간단하게 그림을 통해서 알아보도록 하겠습니다.

Convex cone set을 잘 이해했다면 conic hull이 왜 저런 모양을 가지게 되는지는 바로 이해하실 수 있으리라 생각이 듭니다.
자 그렇다면 convex optimization의 기본이 되는 집합 구조에 대해서 알아보았고 조금 더 응용된 예시를 한번 살펴보도록 하겠습니다.
2. Convex Set Examples
Examples of convex sets
- empty set, any single point, whole space ($\mathbb{R}^{n}$) 등은 모두 affine set입니다. 따라서 convex set입니다. 직관적으로 받아들일 수 있을 것 같네요.
- 임의의 line은 모두 affine set입니다. 특히 원점을 지나는 직선은 vector space라 볼 수 있고 따라서 convex cone입니다.
- 임의의 line segment는 convex set이지만, affine set이 될 수는 없습니다.
- 임의의 subspace는 affine 하면서 동시에 convex cone입니다. subspace의 정의 자체가 linear combination에 갇혀 있는 집합이기 때문에 subspace의 정의만 잘 알고 있다면 이해할 수 있을 것 같습니다.
Hyperplane and Halfspaces
Hyperplane은 초평면으로 우리가 상상할 수 없는 초공간 내에서 정의되는 linear space라 보면 됩니다. 2차원 평면에서 정의가 된다면 직선, 3차원 공간에서 정의가 된다면 평면... 이런 식으로 말이죠. 정의 자체는 간단합니다.
- $\{ x\,|\,a^{\rm{T}}x=b\} ,a\in \mathbb{R}^{n},\;a!=0,b\in \mathbb{R}$
여기서 $a$는 hyperplane의 법선벡터로 평면 내부에 존재하는 모든 벡터와 수직의 관계를 이루는 중요한 벡터입니다. 평면의 방향을 결정한다고 볼 수도 있죠. 그다음으로 $b$는 원점으로부터 평면이 어느 정도 offset을 가지는 지 결정해 주는 상수 값입니다.

Hyperplane을 2차원으로 단면화를 했을 때는 저렇게 보이겠죠. hyperplane은 affine set입니다. 그리고 hyperplane은 whole space를 나누는 경계 역할을 수행할 수 있습니다. 직관적으로 평면 아래와 위로 나뉘겠죠? 이때 나눠지는 공간들을 우리는 halfspace라 정의합니다.
- $\{ x\,|\,a^{\rm{T}}x\leq b\} ,\{ x\,|\,b \leq a^{\rm{T}}x\} $
이 때 등호가 성립하면 closed half space이고 성립하지 않으면 open half space라 볼 수 있습니다. half space는 분명 무한한 집합이지만 affine set은 아닙니다. (affine set은 infinite set이지만 모든 infinite set이 affine set인 것은 아닙니다.)

$a^{\rm{T}}x\leq b$ 부근에서 half space를 벗어나는 line은 존재하기 때문에 affine set이 될 수 없습니다. 다만 convex set 인 것은 맞습니다.
Euclidean balls
Euclidean balls는 공이라 생각하면 되는데, 2차원 평면에서는 원, 3차원 공간에서는 구, 고차원 공간에서는 ball 이렇게 부르는 것 같습니다. 정의 자체는 친숙합니다. ball에 해당하는 중심이 있고 그 중심과의 거리가 $r$ 이하에 해당하는 point들의 집합이라 보면 됩니다.
- $\mathbf{B}(x_{c},r)=\{ x\,|\,\parallel x-x_{c}\parallel_{2} \leq r\} =\{ x\,|\,(x-x_{c})^{T}(x-x_{c})\leq r^{2}\} $
$x_{c}$가 ball의 중심점이고 $r$이 ball의 반경이라 보면 됩니다. ball은 생긴 것부터 자명하게 convex set 인 것 같지만, 책에 간단한 증명이 나와있으니 한번 정리 해보도록 하겠습니다.
가장 간단하게 어떤 임의의 집합이 convex set임을 보이고 싶다면 임의의 line segment가 set에 포함된다는 것을 보이면 됩니다.
- $\parallel \theta x_{1}+(1-\theta )x_{2}-x_{c}\parallel_{2} \leq r, \; \text{where}, \, 0\leq \theta \leq 1$
- $\parallel \theta x_{1}+(1-\theta )x_{2}-x_{c}\parallel_{2} =\parallel \theta (x_{1}-x_{c})+(1-\theta )(x_{2}-x_{c})\parallel_{2} $
- $\parallel \theta (x_{1}-x_{c})+(1-\theta )(x_{2}-x_{c})\parallel_{2} \leq \parallel \theta (x_{1}-x_{c})\parallel +\parallel (1-\theta )(x_{2}-x_{c})\parallel $
- $\parallel \theta (x_{1}-x_{c})\parallel +\parallel (1-\theta )(x_{2}-x_{c})\parallel =\theta \parallel x_{1}-x_{c}\parallel +(1-\theta )\parallel x_{2}-x_{c}\parallel $
- $\theta \parallel x_{1}-x_{c}\parallel +(1-\theta )\parallel x_{2}-x_{c}\parallel \leq r$ : $\parallel x_{1}-x_{c}\parallel \leq r,\parallel x_{2}-x_{c}\parallel \leq r$
이기 때문에 결국 $r$ 보다 작다는 것이 증명이 됩니다. 따라서 euclidean ball은 convex set입니다. 증명 과정에서는 삼각 부등식 ($\parallel A+B\parallel \leq \parallel A\parallel +\parallel B\parallel$) 과 euclidean norm의 homogeneity 성질을 활용하였습니다.
Ellipsoids
다음으로는 타원입니다.
- $\{ x\,|\,(x-x_{c})^{\rm{T}}\mathbf{P}^{-1}(x-x_{c})\leq 1\} $ : 이때 $\mathbf{P}$는 symmetric 하며 positive definite입니다.
행렬 $\mathbf{P}$의 고윳값이 타원의 각 차원을 이루는 축이라 보면 됩니다. 2차원이면 단축, 장축 이렇게 구성이 되겠죠?
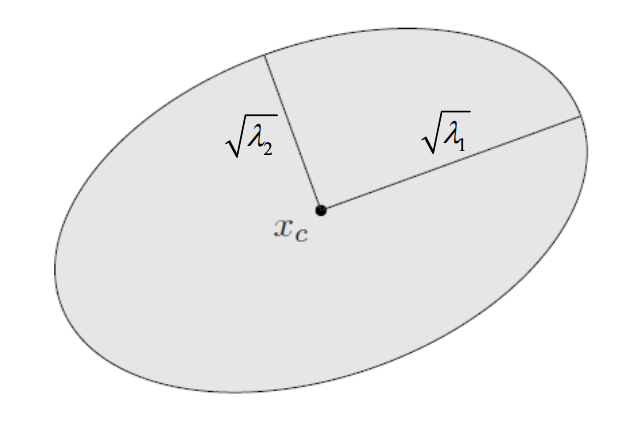
생긴 건만 보면 역시 convex set 인 듯하네요. 증명에 관심 있는 분들은 직접 해보시길 바랍니다.
Norm Cone
Norm Cone이라 불리는 녀석도 있습니다. 다변수 미적분학을 공부했다면 한 번쯤은 봤을 수 있지만, 그렇지 않다면 상상이 잘 안 갈 수도 있습니다. 정의는 간단합니다. Norm cone은 벡터의 크기가 주어진 스칼라보다 작거나 같은 점들의 집합을 나타내며, 최적화 문제에서 제약 조건을 효율적으로 다룰 때 중요한 역할을 합니다.
- $\mathbf{C}=\{(x,t)|\parallel x\parallel_{2} \leq t\} \subseteq \mathbb{R}^{n+1}$
시각화를 해보면 이해가 쉽기 때문에 n=2인 경우를 보여드리겠습니다.
수식 자체는 $\sqrt{x^{2}_{1}+x^{2}_{2}} \leq t$입니다.
$t=0$이라면 그냥 $x_{1}=0,x_{2}=0$ 원점이 되겠네요.
$t=1$이라면 $\sqrt{x^{2}_{1}+x^{2}_{2}} \leq 1$ 반지름이 1인 원이 됩니다.
$t=k$이라면 $\sqrt{x^{2}_{1}+x^{2}_{2}} \leq k$ 반지름이 k인 원이 됩니다.
이러한 구조를 표현하려면 $\mathbb{R}^2$에서는 표현할 수 없겠죠? t에 대한 새로운 축이 존재해야 하기 때문에 $\mathbb{R}^3$에서 정의가 됩니다. 시각화를 해보면 아래와 같습니다.
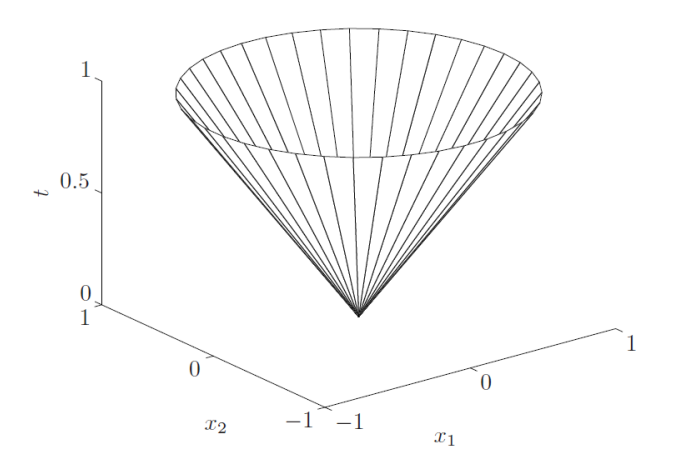
이제야 정말로 콘의 모양을 보여주고 있습니다. 증명은 euclidean ball과 비슷합니다. 이 역시 convex set입니다. 하지만 affine set은 아닙니다.
Polyhedron
다면체는 유한한 개수의 선형 방정식과 부등식의 해집합입니다. 더 쉽게 말하면 유한한 개수의 hyperplane과 halfspace들의 교집합이라 보면 됩니다. 수식은 아래와 같습니다.
- $\mathbf{C}=\{ x\,|\,a^{\rm{T}}_{j}x\leq b_{j},\,j=1,\ldots ,m,c^{\rm{T}}_{j}x=d_{j},j=1,\ldots ,p\} $ : 유한한 선형 방정식과 부등식의 해집합입니다.
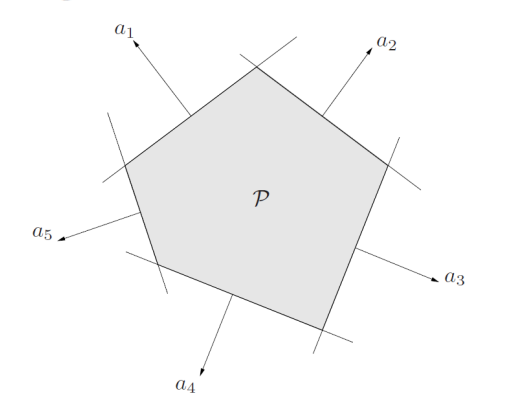
Polyhedra(다면체)는 convex set입니다. Polyhedron은 선형 프로그램의 가능 영역(feasible region)을 나타내며, 선형 부등식으로 정의된 모든 점들의 집합입니다. 최적화 문제의 해는 종종 polyhedron의 꼭짓점에서 발생합니다.
Simplexes
단체를 이해하기 위해서는 affinely independent를 이해해야 합니다. affinely indepdent란 모든 point 간의 line이 independent 해야 한다는 점입니다.
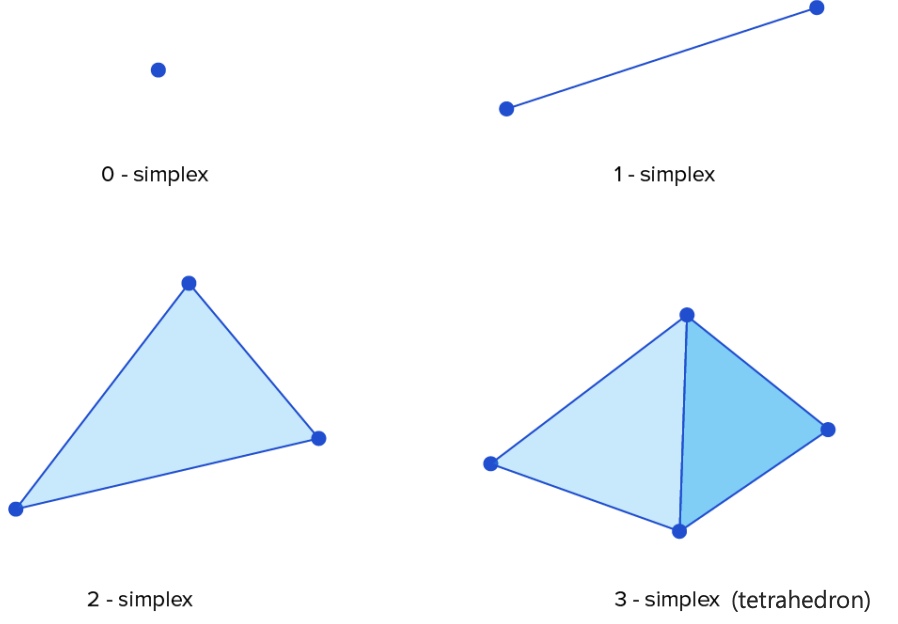
예를 들어 2-simplex는 세 개의 Point로 구성이 되어 있습니다. 세 개의 point 중 임의로 두 point를 잡았을 때 만들어지는 line 들은 모두 다른 방향을 가지고 있으므로 독립입니다. 그래서 결국 $\mathbb{R}^{n}$ 공간에서는 $n+1$개의 affinely indepent point만 존재할 수 있습니다. Simplexes(단체)의 수식은 아래와 같습니다.
- $\mathbf{C}=\{\theta_{0} v_{0}+\ldots +\theta_{k} v_{k}\,|\,\theta\succeq 0 ,1^{\rm{T}}\theta =1\} $
Simplexes 역시 convex set입니다.
3. Operations that Preserve Convexity
마지막으로 convex Set의 convexity를 보존하는 몇 가지 연산들을 살펴보고 이번 글을 마무리하도록 하겠습니다. convexity를 보존하는 것은 왜 중요할까요?
우리가 잘 알고 있는 Convex Set을 이용해서
새로운 Convex Set을 정의하는 데 유용하기 때문입니다.
즉, 어떠한 set은 이게 convex set인지 아닌지 정의 하기 어려워서 돌아가는 방법을 취한다고 보면 됩니다. 우리가 잘 알고 쉬운 convext Set을 가지고 convexity가 보존되는 연산만을 이용해서 복잡하고 어려운 set에 도달할 수 있다면 이 set의 convexity가 보장되기 때문이죠.
4가지 정도 예시를 살펴보도록 하겠습니다.
InterSection
예를 들어 A라는 convex set과 B라는 convex set의 교집합은 마찬가지로 convex set입니다. Polyhedron(다면체) 역시 hyperplane(convex)와 halfspace(convex) 간의 교집합인 것처럼 교집합 연산은 convexity를 보존해주게 됩니다.

증명을 어떻게 해야 하는지는 책에 나와있지 않아 잘 모르겠지만 직관적으로 봤을 때는 이해하는 데 큰 어려움을 없을 것 같습니다.
Affine Function
Affine 함수는 linear function이라 보면 됩니다. $f(x)=Ax+b$ 이런 형태인 것이지요. 이때 임의의 convex set에 affine function을 가해도 그 image는 여전히 convex 합니다. 즉, linear 연산은 convexity를 보존하는 것입니다.
실제로 타원은 unit ball의 affine function이 가해진 꼴이라고 하더군요. Linear 연산은 scaling과 translation이 있습니다. 아마 선형성에 대해서 이해를 하고 있다면 linear 연산이 convexity를 보존시켜 준다는 것은 직관적으로 받아들일 수 있을 것 같습니다.
- 즉, convex set의 affine function이 만들어내는 image는 동일하게 convex 합니다.
- convex set의 affine inverse function이 만들어내는 inverse image 역시 동일하게 convex 합니다.
Perspective functions
Perspective function은 카메라에 상이 맺히는 것과 같이 멀리 있는 물체는 작게 가까이 있는 물체는 크게 원근에 따라 상을 만드는 함수입니다.
따라서, 피사체는 $\mathbb{R}^{n+1}$ 차원의 공간에 있고 상은 $\mathbb{R}^{n}$차원의 평면에 맺히게 됩니다.
우리가 동차 좌표계에서 마지막 원소를 1로 정규화시키고 제거하는 식으로 여기서도 동일하게 사용이 됩니다.
그림을 통해서 한번 예시를 들어보겠습니다. 구를 평면에 투영을 시키면 그림자 같은 것이 생길 것입니다. 그렇다면 그 그림자는 어떻게 생겼을까요? 원이나 타원처럼 생겼겠죠? 역시나 convex set으로 보존이 됩니다.

그림자가 검은색 타원으로 convex set으로 정의가 되었네요.
따라서 어떤 convex set이 있을 때 그것의 perspective image 역시 convex 하며 그 inverse도 성립합니다. 여기서 inverse가 성립한다는 것이 이해가 안 될 수 있습니다. 그렇기 때문에 한번 수학적으로 증명을 해보도록 하겠습니다.
Q. If $\mathbf{C}\subseteq \mathbb{R}^{n}$ is convex, then the inverse image of a convex set under the perspective function is also convex
- $ \mathbf{P}^{-1}(\mathbf{C})=\{(x,t)\in \mathbb{R}^{n+1}\,|\,x/t\in \mathbf{C},\,t>0\} $
일단 원래 convex set에 두 point $\frac{x}{t} ,\frac{y}{s} $가 있을 때, 각각의 inverse image를 $(x,t)$ $(y,s)$라 정의하겠습니다.
- $(x,t)\in \mathbf{P}^{-1}(\mathbf{C}),\,(y,s) \in P^{-1}(\mathbf{C})$
이때 $0\leq \theta \leq 1$에 대해서 우리는 아래의 관계를 증명해야 합니다.
- $\theta (x,t)+(1-\theta )(y,s)\theta \in \mathbf{P}^{-1}(\mathbf{C})$
이것을 증명하는 것은 아래를 증명하는 것과 동치입니다.
- $\frac{\theta x+(1-\theta )y}{\theta t+(1-\theta )s} \in \mathbf{C}$
동치인 이유를 아는 것이 중요한데요,
$\theta (x,t)+(1-\theta )(y,s)\theta = \left( \theta x+\left( 1-\theta \right) y\right) ,\left( \theta t+(1-\theta \right) s)\in \mathbf{P}^{-1}(\mathbf{C})$를 만족하기 위해서는 $\frac{\theta x+(1-\theta )y}{\theta t+(1-\theta )s} \in \mathbf{C}$가 만족되어야 합니다.
$\mathbf{P}^{-1}(\mathbf{C})$의 정의를 살펴보시길 바랍니다.
즉, 이러한 상황에서 우리는 아래와 같이 표현할 수 있는 $0\leq \alpha \leq 1$만 찾을 수 있다면 증명은 완료됩니다.
- $\frac{\theta x+(1-\theta )y}{\theta t+(1-\theta )s} =\alpha (\frac{x}{t} )+(1-\alpha )\left( \frac{y}{s} \right) $
- $\alpha =\frac{\theta t}{\theta t+(1-\theta )s} \in [0,1]$로 설정한다면 가능합니다.
정리하여 $\mathbf{C}$가 convex set이니, persective function의 inverse image인 $\mathbf{P}^{-1}(\mathbf{C})$는 역시 convex set입니다.
Conclusion
일단 이 정도로 Convex Set에 대해서 살펴보았습니다.
글을 전반적으로 보면 알겠지만 선형대수의 중요함이 보이는 부분들이 있습니다.
개인적으로 필요한 부분들은 따로 공부하려고 합니다.
다음번 글은 Convex Function에 대해서 알아보도록 하겠습니다.
'Math > Convex Optimization' 카테고리의 다른 글
| Optimization Theory (Gradient Descent - Convergence Analysis) (2) | 2022.09.08 |
|---|---|
| Optimization Theory (Unconstrained Optimization) (0) | 2022.09.08 |
| Optimization Theory (Convex Optimization Problems) (0) | 2022.05.03 |
| Optimization Theory (Convex Functions Ⅱ) (2) | 2022.04.23 |
| Optimization Theory (Convex Functions Ⅰ) (1) | 2022.04.23 |



