Before Review
이번 논문은 비디오를 이해하는 데 있어 중요하게 작용하는 요소들을 고려하여 새롭게 제안된 attention 메커니즘을 다룬 논문입니다.
Neurips 페이퍼는 Core-ML 쪽만 다루는 줄 알았는데 Vision 연구도 다루나 봅니다.
리뷰 시작하도록 하겠습니다.
Introduction
우리가 자주 사용하는 Convolution은 Computer Vision을 입문한 사람들은 모두 다 들어봤을 정도로 많이 사용됐고, 되고 있습니다. 지난 수십 년간 비전 시스템에 있어서 딥러닝 연구의 부흥을 책임진 부분이기도 합니다. 하지만 최근 연구에서는 Transformer 기반의 모델이 많이 등장하면서 Convolution과의 비교가 많이 진행 되었습니다.
Feature Transform 관점에서 Convolution의 한계는 convolution kernel의 stationarity로 인해 발생하는 문제입니다. 고정된 크기의 kernel을 가지고는 다양한 동적 변화를 수행할 수 없다는 것이 바로 한계점입니다. 이러한 단점을 보완하고자 Dynamic convolution, Self attention 기법 등 dynamic feature transform을 위해 다양한 후속 연구들이 진행되고 있었습니다.
특히 Self-attention을 활용한 vision transformer(ViT)가 이미지 도메인에서 성공적인 모습을 보여주고 있습니다. 그래서 비디오 진영에서도 spatio-temporal convolution 방식을 spatio-temporal self attention 방식으로 대체하여 비디오의 long-range dependency를 해결하려는 연구들이 많이 진행되었습니다.
하지만 그럼에도 비디오를 이해하기에는 부족한 면이 있다고 합니다. Video Understanding에 중요한 motion 정보를 파악하는 것도 개선의 여지가 많이 남아 있다고 하네요. 예를 들면 spatio-temporal self attention은 positional embedding이 없다면 motion representation을 학습하기 어렵고 positional embedding이 있다고 해도 Something-Something 벤치마킹에서는 효과적이지 않은 것을 확인할 수 있습니다.
본 논문에서는 이전의 work들이 Video Understanding 측면에서 부족함이 있다는 것을 밝히고 비디오의 spatio-temporal 관계 속에서 rich construction을 이용하는 방법을 제안합니다.
우선 알아둬야 하는 배경 지식들이 좀 있어 Related work와 비교 방법론에 대한 설명을 충분히 마친 후 제안된 RSA(Relational Self Attention)에 대한 얘기를 시작하도록 하겠습니다.
Related Works
비디오 관련 논문을 꽤 읽었다고 생각했는데 related work을 보니 모르는 부분도 많고 나름의 고찰을 얻었던 것 같습니다. Video Understanding 연구 분야의 흐름을 정리할 수 있도록 related work도 간단하게 다루도록 하겠습니다.
Convolution and its variants
기본적인 Convolution 연산이 딥러닝 연구를 지배했었고 현재에도 많이 사용되는 것은 사실입니다. 다만, static kernel에 의해 표현력이 제한되는 것은 vision transformer 붐이 일어나면서 많이들 알려진 사실입니다. 그래서 Input feature에 맞춰서 동적으로 반응하는 dynamic feature transform이 연구되고 있습니다.
Involution이라고 해서 뒤에서 조금 더 자세히 설명할 예정이지만 한 줄 요약하자면 light weight dynamic kernel을 이용해서 기존 convolution 대비 적은 연산량을 가져가면서 대체적으로 좋은 성능을 달성한 방법이 있습니다.
저자가 제안한 RSA(Relational Self Attention)은 비디오의 시공간적 구조에서 relational pattern에 집중하는 점에서 이렇게 kernel을 사용하는 방식과는 차별점이 있다고 하네요.
Self-attention and its variants
Self-attention 연산은 원래 long-range interaction이 중요하게 작용하는 기계 번역(자연어처리)을 위해 고안된 방법론입니다. 하지만 그 다양성과 확장성 덕분에 다양한 도메인에서 널리 사용되고 있습니다.
Convolution 연산을 Self attention 연산으로 대체한 Vision Transformer(ViT)는 Image Understanding 분야에서 꽤나 좋은 성과를 보여주고 있습니다.
Self-attention을 확장한 연구들 중에는 Spatial attention을 channel-wise attention으로 확장하여 좋은 성능을 보인 연구가 있습니다. 또한 lambda layer라는 것을 설계하여 visual contents와 relative position embedding 간의 상호관계를 softmax 함수 없이 인코딩할 수 있어 self-attention의 연산보다 뛰어난 성능을 보인 방법도 있습니다.
본 논문에서 제안된 RSA(Relational Self Attention)은 이러한 연구들의 확장판이라고 볼 수 있습니다. 다만, 초점을 rich relational feature를 인코딩할 수 있게 설계된 방법론이라고 보면 됩니다.
Convolution and self-attention for video understanding
이제 좀 비디오에 관련된 얘기를 해보면 이미지에 Image Classification이라는 중요한 task가 있는 것처럼 비디오에는 Action Recognition(Video Classification)이라는 task가 있습니다. 단순히 멈춰있는 장면을 보고 예측을 하는 것이 아니라 프레임의 흐름에 따른 action의 의미론적인 정보를 이해하는 것이 중요한 task라 temporal dynamics를 잘 인코딩하는 것이 중요합니다.
비디오는 이미지와는 달리 시간이라는 하나의 차원이 증가하기 때문에 일반적으로 사용하는 2D Convolution이 아니라 3D Convolution을 통해서 spatio-temporal feature를 얻게 됩니다. 이미지와 비슷하게 3D convolution 말고도 Self-Attention을 통해서 진행이 되기도 합니다.
하지만 3D Convolution, Self-Attention 모두 temporal dynamics를 modeling 하기에는 부족한 면이 있다고 합니다. 저자가 제안하는 RSA도 이러한 한계점을 보완하고자 제안이 되었다고 보시면 됩니다.
Learning motion for video understanding
많은 비디오 관련 task에서 사용하는 data에는 단순히 RGB frame 뿐만 아니라 optical flow도 같이 사용하게 됩니다. 프레임들이 시간의 흐름에 따라 어떤 식으로 변화하는 지를 알아야 하기 때문이죠.
즉, 비디오에서 발생하는 motion에 대한 정보를 취득하기 위함이라 볼 수 있습니다. 일반적으로 optical flow를 사전에 뽑고 gradient가 전달이 안 되는 방식으로 사용하고 있는데 최근 연구들에서는 모델 내부적으로 motion representation을 학습하도록 설계하는 추세인 것 같습니다.
네트워크 내에서 feature-level의 optical flow를 추정하는 방식도 있고, 단순히 연속적인 frame-wise feature의 차이를 계산하는 방식도 있다고 합니다.
저도 처음 알았는데 픽셀끼리의 관계를 이용하여 motion-likelihood map을 활용하여 motion-centric action recognition 분야에서 sota 성능을 달성한 방법도 있다고 합니다.
Background
논문에서 제안하는 attention을 설명하기에 앞서 우선 비교 방법론에 대한 이해가 필요하니 저자가 간략하게 설명을 적어 놓았습니다.

기본적으로 feature transform의 역할은 시간/공간 순서를 보존하면서 feature map을 update 하는 것입니다. Feature map의 각 position에서 이웃 정보를 활용하여 연산되는 구조로 보통 진행됩니다.
간단히 용어 정의하고 각 transform 구조에 대해서 알아보도록 하겠습니다.
- $ X\in R^{T\times H\times W\times C}$ : video의 입력 feature map을 의미합니다.
- $ x_{t, h, w}$ : 특정한 시공간 위치 $(t, h, w)$에서 individual feature를 의미하고 transform을 가해줄 target으로 정의됩니다.
- $\{ x_{t^{\prime }, h^{\prime }, w^{\prime }}\}_{(t^{\prime }, h^{\prime }, w^{\prime })\in N_{(t, h, w)}} $ : 특정한 시공간 위치 $(t, h, w)$ 근처에 있는 feature 들로 context information으로 정의됩니다.
여기서 notational convenience를 위해 다음과 같이 간략하게 표현하도록 하겠습니다.
- transform target : $ x_{n}\in R^{C}$ , $ n $은 특정한 시공간 위치를 나타냅니다.
- context information : $ X_{n}\in R^{M\times C}$ , $ M $은 neighborhood의 사이즈를 의미합니다. Convolution을 예로 들면 kernel size라고 생각하시면 됩니다.
여기서 우리는 이제 feature transform을 다음과 같은 관계로 정의하겠습니다.
"학습 가능한 파라미터 $ W $를 지닌 함수 $ f $와 context $ X_{n}$를 이용해 target $ x_{n}$을 출력 $ y_{n}$로 투영시키는 것"
자 이제 최근 자주 사용되는 transform 구조에 대해서 먼저 알아보도록 하겠습니다.
Convolution
가장 익숙하고 간단한 Convolution 구조입니다. Convolution은 static 하지만 translation-equivariant 한 feature transform이라는 특징을 가지고 있습니다.
Static 하다는 것은 크기가 일정한 kernel로 연산을 수행한다는 의미입니다. Translation-equivariant 하다는 것은 말 그래도 input에서 위치가 달라져도 output이 동일하다는 의미입니다. 고양이가 이미지 상단에 존재하든, 하단에 존재하든 우리는 적당한 CNN 네트워크를 통해 고양이라고 분류할 수 있습니다. 이유를 간단하게 설명하면 Max pooling과 Softmax를 취하기 때문입니다.
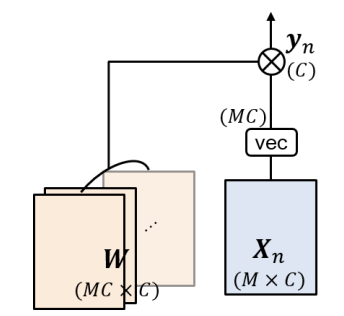
보통은 kernel을 여러 개 사용하는 구조로 다양한 visual pattern을 찾는 것을 목표로 합니다.
하지만 Convolution은 target $ x_{n}$으로부터 영향을 받지 않는다는 구조를 가지기 때문에 여전히 정적(static)입니다. 표현이 조금 애매한 감이 있는데 뒤에 Self-Attention 메커니즘을 확인하면 정적이다라는 표현이 무엇인지 조금 더 잘 이해할 수 있을 것 같습니다.
Self-Attention
Self-Attention은 입력 target $ x_{n}$와 그 주변 정보인 context $ X_{n}$의 content-to-content interaction을 통해 attention map을 생성합니다. 여기서 Convolution과 차이가 발생합니다. Convolution에서 사용하는 kernel은 static 한 kernel(target으로부터 생성되지 않고 독립적으로 존재)인 반면, Self-Attention의 attention map은 target과 context의 interaction으로부터 만들어집니다. Target이 어떤 값을 가지고 있는지에 따라 동적으로 변하기 때문에 Dynamic transform이라 정의됩니다.
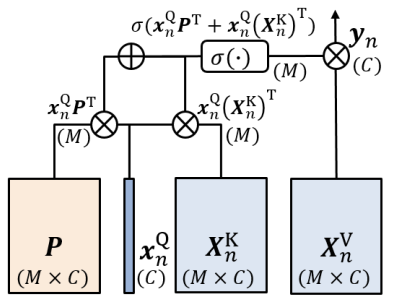
Self-Attention 연산은 기본적으로 입력 target $ x_{n}$을 Query로 임베딩 시키고, context $ X_{n}$를 Key와 Value로 임베딩 시킵니다. 우선 Query와 Key를 가지고 attention score를 계산합니다. 그리고 여기에 Positional Encoding(content-to-position) 정보를 더해서 위치 정보를 추가합니다.
- $ softmax(x^{Q}_{n}(X^{K}_{n})^{T}+x^{Q}_{n} P^{T})$
위와 같은 방식으로 attention map 즉, 동적인 kernel을 생성했다면 이를 가지고 value embeddings를 축약시킵니다. Context 정보 전부를 축약시킬 때 attention map을 통해 어디 어디에 집중을 해야 하는지 파악하는 것이죠.
- $ softmax(x^{Q}_{n}(X^{K}_{n})^{T}+x^{Q}_{n} P^{T})x^{V}_{n}$
Convolution과 다른 점은 바로 attention map을 생성할 때 context와 target 정보를 바탕으로 만들어지기 때문에 kernel이 dynamic 하게 생성된다는 점입니다.
Involution
Involution은 이번 논문을 통해서 처음 알게 된 transform 구조인데 light-weight dynamic transform이라 보면 됩니다. Self-Attention 같은 경우는 content-to-content interaction을 통해서 attention map을 만들었고, content-to-position을 통해서 positional encoding을 생성했습니다.
Involution은 여기서 content-to-position 만을 사용한다고 합니다. 기존 self-attention 방식에서 cotent-to-position을 할 때는 learnable matrix를 사용하는 것이 아니라 주기함수를 이용해서 그 값을 부여하는 것으로 알고 있었습니다. 여기서 궁금한 것은 learnable matrix를 이용해서 positional 정보를 부여한다고 합니다. 왜 이런 차이가 있는지 궁금하네요.

Involution은 target과 learning matrix를 통해서 kernel을 생성합니다. 이 역시 target의 정보가 들어가기 때문에 dynamic transform입니다.
- $\kappa^{v}_{n} =x_{n} P^{T}$
그리고 생성된 dynamic kernel을 context에 적용시켜 줍니다. 전체적인 느낌은 Self-attention과 비슷한데 과정이 상당히 간소화된 느낌이라 light-weight dynamic transform이라 부르는 것 같습니다.
- $ y_{n}=\kappa^{v}_{n} X_{n}=x_{n} P^{T} X_{n}$
Lambda convolution
Lambda convolution은 Involution과 굉장히 비슷합니다. 다만 dynamic kernel을 생성할 때 target과 learnable matrix가 아닌 context와 learnable matrix를 토대로 만들어 냅니다.
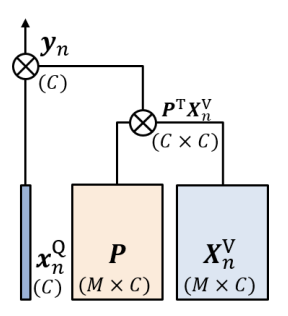
Self-attention과 비슷하게 Query와 Value로 임베딩 시킵니다. 여기서 content-to-content interaction은 사용하지 않기에 key는 필요 없습니다. 그리고 Value와 learnable matrix $ P $를 가지고 dynamic kernel을 생성하고 이것을 가지고 key를 embedding 시킵니다.
- $ y_{n}=x^{Q}_{n}\lambda^{P}_{n} =x^{Q}_{n} P^{T} X^{V}_{n}$
Involution과 Lambda convolution은 연산 순서에서 차이가 있을 뿐 개념 자체는 비슷합니다. Self-attention 과는 다르게 softmax non-linearity를 가지지 않습니다. Image-Classification 분야에서 Involution과 Lambda convolution은 일반 convolution과 Self-attention의 성능을 능가하는 연구가 이미 있다고 하네요.
Limitation of existing dynamic transforms
앞서 언급한 방법들은 convolution을 제외하고 모두 dynamic transform입니다. 즉 content-to-content interaction을 사용하거나, content-to-position을 사용하여 dynamic kernel을 생성한다는 것입니다. 이러한 방식이 image domain에서는 꽤나 효과적이지만 video domain에서는 부족한 면이 있다고 합니다.
가장 큰 문제는 content-to-content interaction이 바로 부분적으로 나뉜다는 것입니다.
- $ x^{Q}_{n}\left( X^{K}_{n}\right)$
예를 들어 self-attention 방식에서 query와 key는 individual element의 correlation만을 고려합니다. 이러한 구조가 video의 spatio/temporal 구조를 이해하는 상황에서 적합하지 않다고 저자는 주장합니다.
또한 content-to-positon interaction 역시 당연하게 비디오의 global information을 고려하지 않고 생성됩니다.
결국 spatio-temporal content나 generic motion information을 잘 capture 하기 위해서는 video의 global 한 정보를 토대로 relational pattern을 이해하는 것이 핵심이라 볼 수 있습니다. 그럼 이제부터 저자가 제안하는 RSA(Relational Self Attention)은 과연 그 문제를 해결할 수 있는 구조인지 확인해 보도록 하겠습니다.
Method
Self attention과 비슷하게 Query, Key, Value embedding을 사용합니다.
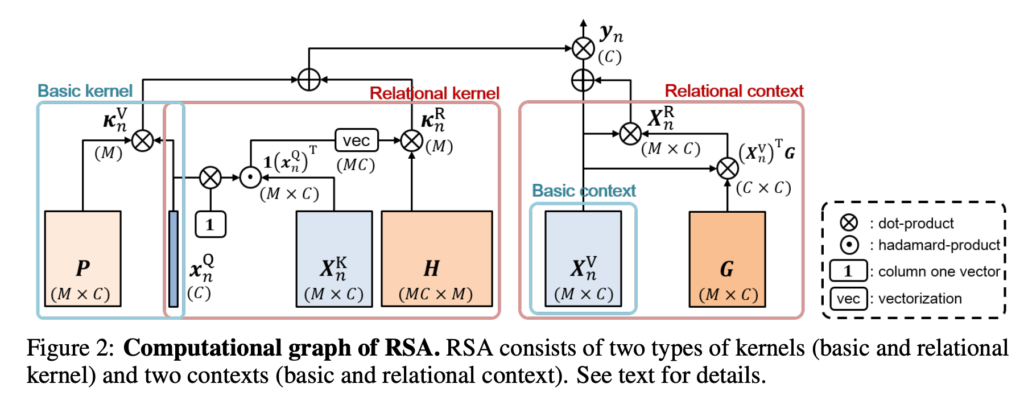
RSA는 Relational kernel과 Relational content로 구성됩니다.
Relational Kernel
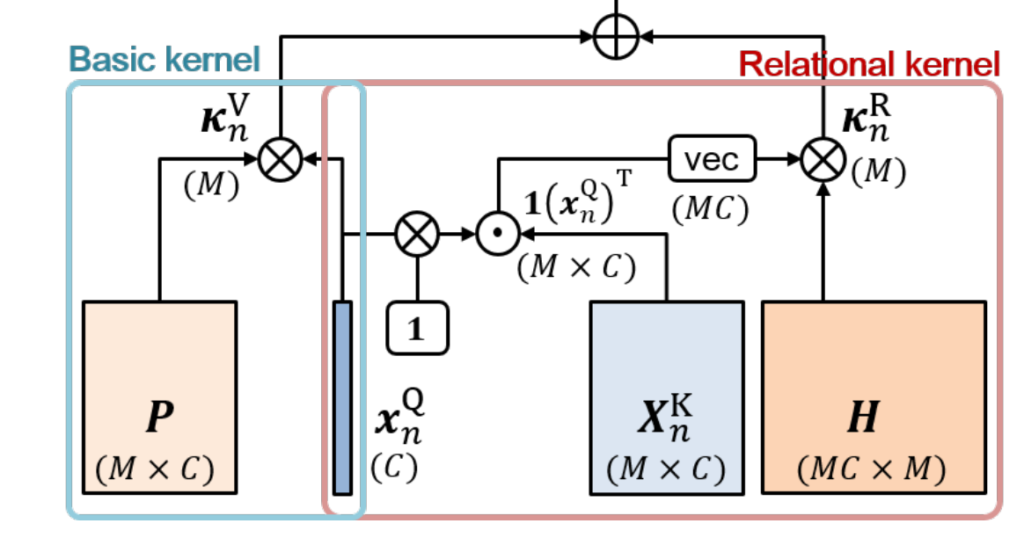
Relational kernel은 content-to-content interaction을 통해 context의 관련성을 좀 더 global 하게 예측하는 것에 목적이 있습니다. 복잡하게 이를 수행하는 것보다 여기서는 fully connected layer를 통해서 embedding을 시키는 것 같습니다.
- $\kappa^{R}_{n} =x^{Q}_{n}\left( X^{K}_{n}\right)^{T} H $
여기서 $ H $가 Identity Matrix라면 기존 self-attention과 동일하다고 보면 됩니다.
결국 $ H $를 통해서 local-global 순으로 kernel을 다시 만든다고 보면 됩니다.
여기서 단순히 dot-product를 통해 계산하면 semantic information을 잃을 수 있다고 적혀 있습니다. 정확히 무슨 의미인지는 파악을 못해서 일단 넘어가겠습니다. 무튼 dot-product가 아닌 Hadamard product를 통해서 연산을 진행해 주면 semantic information을 살릴 수 있다고 하네요.
- $\kappa^{R}_{n} =vec(1(x^{Q}_{n})^{T}\odot X^{K}_{n})H $
그 둘의 차이는 미묘하게 다른데 Hadamard product은 element wise product을 생각하면 됩니다.
Dot product : $ x^{Q}_{n}\left( X^{K}_{n}\right)^{T} $
Hadamard product : $1(x^{Q}_{n})^{T}\odot X^{K}_{n}$
Dot product를 하면 아래와 같은 결과가 나오고

Hadamard product를 하면 아래와 같은 결과가 나옵니다.
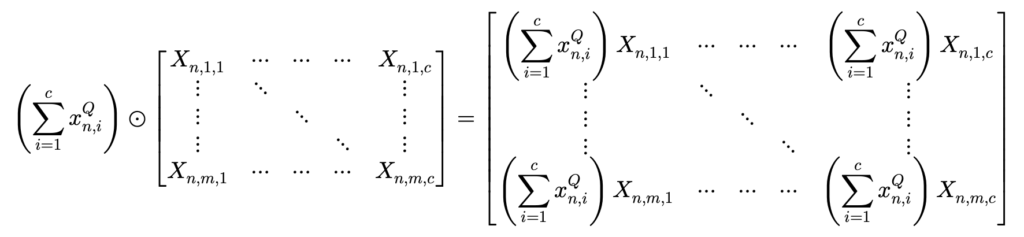
Query의 summation을 각 element 마다 살려서 곱해주는 것이 semantic information을 살려주는데 더 도움이 된다고 하는 것 같네요. 이 이상은 어떤 의미인지 잘 모르겠습니다.
게다가 softmax function을 제거하면 relational kernel이 negative activation을 가질 수 있어서 더 상대적인 interaction을 잡을 수 있다고 합니다. 즉, 시간의 흐름에 따른 content의 변화를 더 잘 표현할 수 있다는 것이죠.
Relational content
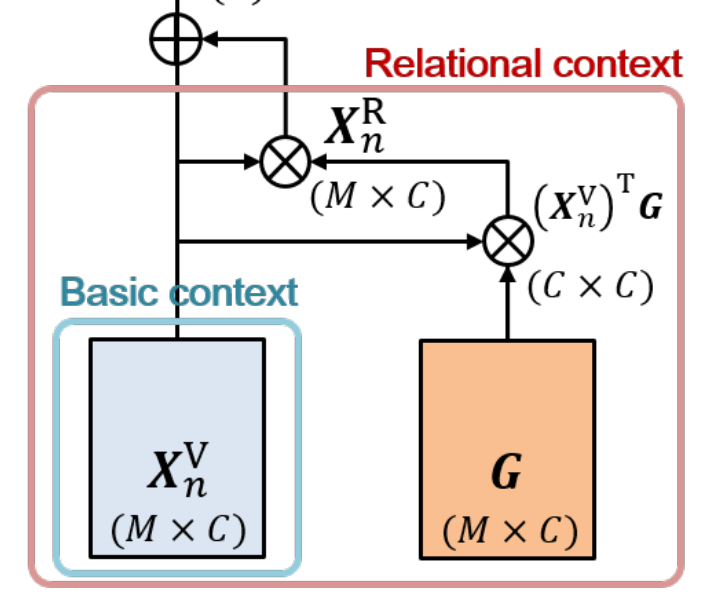
Relational content는 content-to-content interaction에서 relational pattern을 제공하는 것에 목적이 있습니다. 여기서는 Value embedding끼리 correlation을 계산합니다.
- $ X^{V}_{n}(X^{V}_{n})^{T}\in R^{M\times M}$
굉장히 추상적이지만 $ X^{V}_{n}(X^{V}_{n})^{T}$는 context 내에서 content-to-content interaction pattern을 나타냅니다.
어떤 context 끼리 서로 반응하는지 나타내는 self-correlation map 이죠. 여기에 fully connected layer를 통해 임베딩을 시켜 더욱 relational 한 content를 만들어냅니다.
기존의 context는 서로 따로 노는 느낌이지만 self-correlation과 embedding을 통해 relation 정보가 추가되었기 때문에 relational content라 기대하는 것이죠.
- $ X^{R}_{n}=X^{V}_{n}(X^{V}_{n})^{T} G\in R^{M\times M}, G\in R^{M\times C}$
이렇게 해서 relational kernel과 relational content를 만들 수 있었습니다. 결국 핵심은 적절한 임베딩을 통해 local 정보뿐만 아니라 global 정보가 어떻게 상호작용하는지 알려주는 것이라 볼 수 있습니다.
Combining of difference types of kernels and contexts
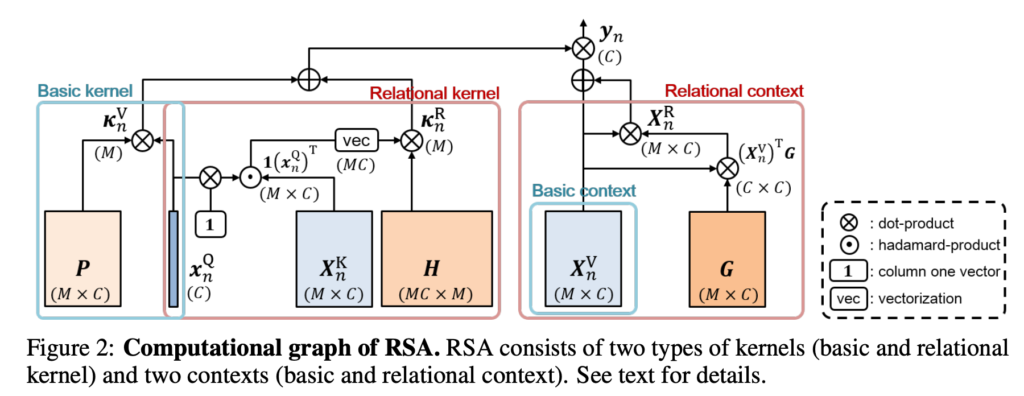
Relational kernel과 Relational content를 가지고 dynamic transform을 수행하면 아래와 같습니다.
- $ y_{n}=\left( \kappa^{V}_{n} +\kappa^{R}_{n} \right) \left( X^{V}_{n}+X^{R}_{n}\right) $
그리고 뜯어보면 아래와 같습니다.
- $ y_{n}=\kappa^{V}_{n} X^{V}_{n}+\kappa^{R}_{n} X^{V}_{n}+\kappa^{V}_{n} X^{R}_{n}+\kappa^{R}_{n} X^{R}_{n}$
$\kappa^{V}_{n} X^{V}_{n}$는 Involution과 동일한 구조입니다.
$\kappa^{R}_{n} X^{V}_{n}+\kappa^{V}_{n} X^{R}_{n}$는 cotent to relation 구조를 capture 하는 transform이라 볼 수 있겠네요.
마지막 $\kappa^{R}_{n} X^{R}_{n}$은 relation to relation 구조를 capture 하는 transform입니다.
이렇게 4가지의 transform으로 분해할 수 있고 풍부한 transform 덕분에 video의 rich relational interaction을 인코딩할 수 있다고 하네요. 과연 정말 그런지 실험을 통해 확인해 보도록 하겠습니다.
Experiments
Dataset
Something-something v1 & v2 (SS-V1 & V2)
action recognition benchmark로 motion centric dataset이라 보면 됩니다. 예를 들어 'pushing something from left to right'이라는 클래스가 있을 정도로 fine-grained motion을 이해하는 것이 중요한 데이터셋입니다.
Diving-48
비슷하게 fine-grained action benchmark로 temporal modeling에 크게 의존하는 dataset입니다. 원래 데이터의 라벨이 부정호가 해서 수정된 버전으로 benchmarking을 했다고 하네요.
FineGym
마찬가지로 fine-grained action benchmark로 gymnastic에 대한 action을 담은 비디오 데이터 셋입니다.
Comparison with other transform methods
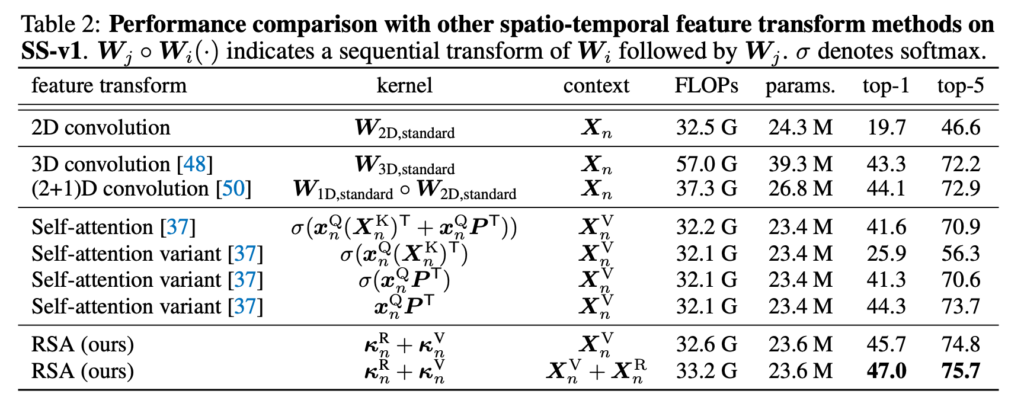
저자가 제안하는 RSA transform과 다른 dynamic transform 간의 비교입니다.
우선 2D convolution으로는 비디오의 temporal 한 정보를 encoding 할 수 없으니 가장 성능이 떨어지는 모습을 보여주고 있습니다. 그다음으로 3D Convolution이나 (2+1) D Convolution의 성능을 보여주고 있는데 생각보다 높아서 놀랐습니다.
다음으로 Self-attention과 variants들의 성능입니다. 인상 깊은 것은 Self-attention에서 Positional Encoding 정보를 제거하면 성능이 (41.6->25.9)로 나락을 가버리네요. Self-attention이 꽤나 content to position에 의존적인 것을 확인할 수 있었습니다.
신기한 건 Query와 Key 간의 interaction을 제거하고 Positional encoding만 사용해도 성능이 어느 정도 나온다는 것입니다. 여기에 softmax를 제거하면 성능이 꽤 큰 폭으로 상승하는데 이는 확실히 negative activation을 통한 더 상대적인 관계를 인코딩할 수 있기에 발생하는 것 같습니다.
최종적으로는 RSA가 가장 좋은 성능을 보여주면서 relational kernel + relational content 조합이 state-of-the-arts를 달성해주고 있습니다.
Comparison to the state-of-the-art methods
다른 sota 방법들과의 benchmarking입니다.
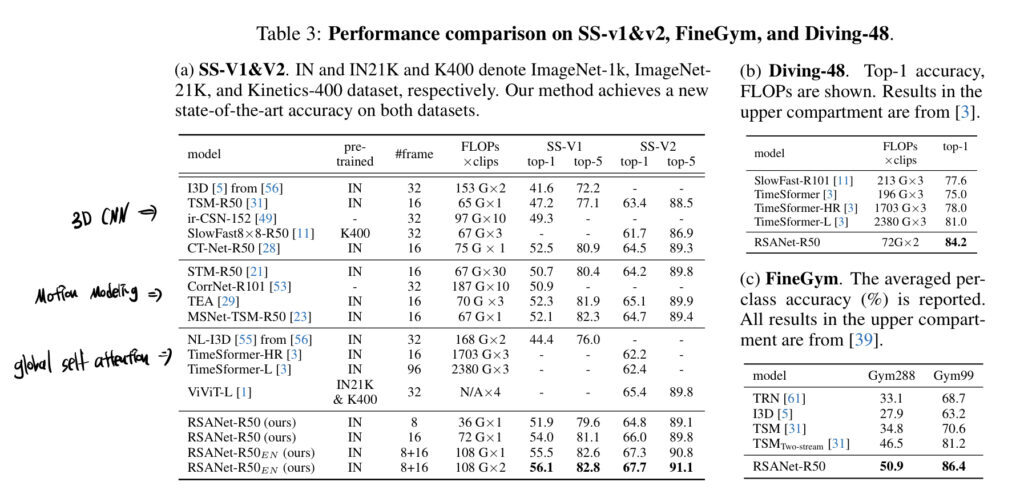
인상 깊은 건 저희 작년 에트리 과정의 큰 부분이었던 TimeSformer에 비해 적은 FLOPs를 가져가면서 더 좋은 성능을 보여주고 있네요. 세 가지 데이터셋에서 정확도 면에서는 가장 뛰어난 성능을 보여주고 있고 FLOPs 역시 괜찮게 가져가고 있네요.
Ablation studies
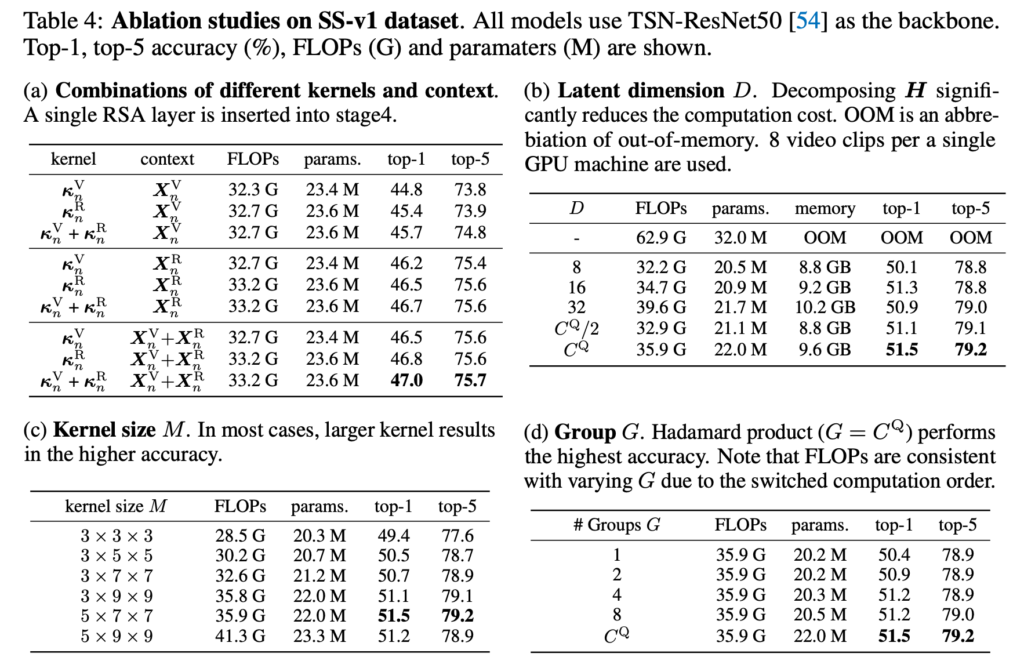
Ablation (a)를 보면 kernel과 context의 다양한 조합을 가지고 실험을 진행했습니다.
Context $ X^{V}_{n}$을 고정하고 kernel을 순서대로 변경했을 때 basic kernel 보다 relataional kernel이 더 성능이 높고, relational kernel을 단일로 사용하는 것보다는 함께 사용해서 transform을 했을 때의 성능이 더 높게 나왔습니다. 나머지 실험의 경향성도 동일합니다.
결국 최종적으로 모든 kernel과 모든 context를 조합해서 transform 한 것이 가장 성능이 높게 나왔습니다.
개인적으로 이 데이터셋의 난이도가 얼마나 어려운지를 제가 잘 모르니깐 이 정도의 성능 향상이 어느 정도 느낌인지는 파악이 잘 안 되네요.
나머지 ablation은 hyper-parameter에 대한 실험입니다.
kernel Visualization

저는 여기가 해석하기 제일 어려웠습니다. 어떻게 실험을 한 건지도 잘 이해가 가질 않네요...
우선 사진에서 노란색으로 칠해진 부분은 Context에 해당하고 빨간색으로 칠해진 부분은 target에 해당합니다. 그리고 Self-attention Kernel과 Basic Kernel 마지막으로 Relational Kernel을 시각화해서 비교합니다.
일단 Self-Attention kernel 같은 경우는 softmax operation이 들어가다 보니 negative activation(파란색)이 존재하지 않습니다. 따라서 상대적으로 변화에 대한 대비가 극명하게 나타나지 않는 것 같습니다.
개인적으로 Basic Kernel과 Relational Kernel 같은 경우는 큰 차이가 보이지 않아 어떻게 해석을 해야 할지 모르겠네요.
일단 Self-Attention에 비해 Relational Kernel이 motion의 변화에 따라 Kernel이 더욱 민감하게 반응을 한다고 정리하면 될 것 같습니다.
Conclusion
평소에 읽었던 비디오 논문이랑 조금 다른 느낌의 논문이라 읽는데 조금 어려움을 겪었습니다.
하지만 본 논문을 통해 Video 데이터를 가지고 응용 논문(action localization, video retrieval)만이 아니라 이렇게 좀 더 core level의 논문을 읽어주는 것도 중요하다는 생각이 들었습니다. 흥미도 조금 가구요.
이상으로 리뷰 마치도록 하겠습니다.



