Before Review
이번 논문은 Video Summarization 분야로 key-frame selection을 optimization 방법론으로 해결한 논문을 가져왔습니다. 비디오팀 논문 방향이 살짝 수정이 되어서 , Video의 Key-frame을 어떻게 하면 잘 뽑을 수 있을까 찾아보다가 이 논문을 읽게 됐습니다.
비디오 같은 경우는 모든 frame을 읽을 필요는 없고 사실 읽어서도 안됩니다. Computation과 memory가 감당할 수 없기 때문입니다. 분명 비디오를 이해하는 데 보다 더 중요한 frame들이 존재할 것이고 , 이러한 frame을 우리는 key-frame이라 부릅니다. key-frame selection(extraction)은 결국 Video Summarization 분야에 속하는 방법론으로 비디오 이해에 좀 더 도움이 되는 Key-frame을 어떻게 추출할까 를 다루는 거라고 보시면 될 거 같습니다.
Introduction
우선 , 이 논문은 2015년도에 나온 논문입니다. 15년도의 분위기가 어땠는지는 모르지만 당시에도 비디오 콘텐츠의 증가로 인한 Video-Understanding에 대한 연구 중요성이 나오던 시기였던 거 같습니다. 사실 비디오 콘텐츠 들은 굉장히 다양합니다.
구조적으로도 다양할 수 있고 , 카메라 모션에 대해서도 , 비디오 길이에서도 천차만별입니다. 또 비디오 데이터 같은 경우는 별로 중요하지 않은 , 중복되는 프레임이 상당수 존재하게 됩니다. 최근까지도 비디오의 이런 redundant 한 성질로 인해 sampling 해서 사용하고 있는 상황인데 15년도 라면 아마도 Video Summarization에 대한 연구 필요성이 강조가 되었을 것 같습니다.
당시에 Summarization은 key-frame으로 뽑아줄 frame의 개수를 static 하게 즉 , 사전에 미리 정해두고 진행했다고 합니다. 하지만 비디오는 앞서 말씀드린 것처럼 비디오의 길이도 다양하고 , 구조적으로도 다양하기 때문에 이러한 접근은 좋지 않습니다. 비디오마다 dynamic 하게 Summarization을 진행할 필요가 있습니다. 아래의 사진을 한번 참고해 보도록 하겠습니다.

video 1의 경우는 비디오 전반적으로 비슷한 장면을 담고 있습니다. 이에 반해 video 2의 경우는 비디오가 다양한 장면을 담아주고 있습니다. 이렇게 비디오의 구조가 다른 상황에서 고정된 summarization을 진행한다면 당연하게도 모든 비디오 데이터셋에 대해서 일반성을 가지기 힘들 것입니다.
따라서 본 논문의 저자는 이렇게 비디오마다 adaptive 하게 key frame을 추출하기 위해서 optimization-based framework를 제안하게 됐습니다.
이때 비디오 summarization의 quality를 평가하기 위한 두 가지 척도인 1) Representativeness , 2) Uniqueness를 고려해주는 데
- Representativeness : Summarization은 비디오에 속해있는 넓은 spectrum의 event를 표현할 수 있어야 함
- Uniqueness : Summarization으로 추출된 frame들은 unique 한 information을 담아야 함 , 즉 각각의 Frame이 나름 distinct 해야 한다는 의미

따라서 제안된 framework에서는 저런 Summarization의 Representativeness와 Uniqueness가 극대화될 수 있도록 최적화시켜주는 방법을 사용하고 있습니다. 자세한 건 뒤에서 다시 다루도록 하겠습니다.
본 논문의 핵심 Contribution을 정리해보면 Static 하게 Video를 Summarization 하는 당시 방법론들과는 반대로 비디오마다 adaptive 하게 , dynamic 하게 summarization을 할 수 있는 framework를 제안한 것에 있는 것 같습니다.
Preliminaries
위에서 Optimization이 핵심 Method인 만큼 본 논문에서 수학적인 개념이 적지 않게 등장하게 됩니다. 따라서 본 논문의 이해를 돕기 위해 필요한 수학적인 개념에 대해서 먼저 짚고 넘어가도록 하겠습니다.
Set Function
집합 함수입니다. 집합을 실수로 사상시키는 관계를 나타낸다고 보시면 됩니다. 집합이 왜 등장하냐면 key frame selection을 통해서 만들어진 key frame의 집합이 전체 집합의 부분집합인 상황이니 , 이러한 집합의 개념이 등장했다고 보시면 됩니다.
이따 소개하겠지만 본 Paper의 목적함수도 이 Set Function의 형태를 가지고 있습니다.
예를 들어 이러한 집합이 있다고 가정해보겠습니다. $ Z=\{ z_{1},z_{2},\cdots ,z_{n}\} $ 이때 , 이 집합 $ Z $를 가지고 만들어줄 수 있는 부분집합의 가짓수는 몇 가지일까요?
$\{ \phi \} ,\{ 1\} ,\{ 2\} ,\{ 3\} ,\{ 1,2\} ,\{ 1,3\} ,\{ 2,3\} ,\{ 1,2,3\} \in \{ 1,2,3\}$ 즉 , $ 2^{n} $ 만큼 가짓수가 생성이 됩니다.
이렇게 원 집합으로 가능한 모든 부분집합을 원소로 가지는 집합을 power set이라고 부르며 $2^{Z}$ 라고 표기를 해줍니다.
이때 , $2^{Z}\longrightarrow \Re $ 이러한 관계를 나타내는 함수를 집합 함수라고 볼 수 있습니다. $ 2^{Z}$의 원소들이 집합이었고 이것이 실수로 반환된다고 보시면 되겠습니다.
Submodular set function
Submodularity는 set function이 가질 수 있는 특성으로 아래의 정의를 만족하는 함수를 의미합니다.
- $ f : 2^{Z}\rightarrow \Re $ 이때 Z는 유한한 집합을 가져야 합니다.
- $ A\subseteq B\subseteq Z , x\in Z-B $
- $ f(B\cup \{ x\} )-f(B)\leqq f(A\cup \{ x\} )-f(A) $ 를 만족하면 f를 submodular set function이라 부릅니다.
그렇다면 저 관계를 만족시킨다는 것이 과연 무엇을 의미하는 걸까요? 하나의 예시를 들어서 설명하도록 하겠습니다. 수질 오염을 검출하기 위해 특정 지역을 담당하는 sensor를 설치하는 상황을 살펴보도록 하겠습니다.
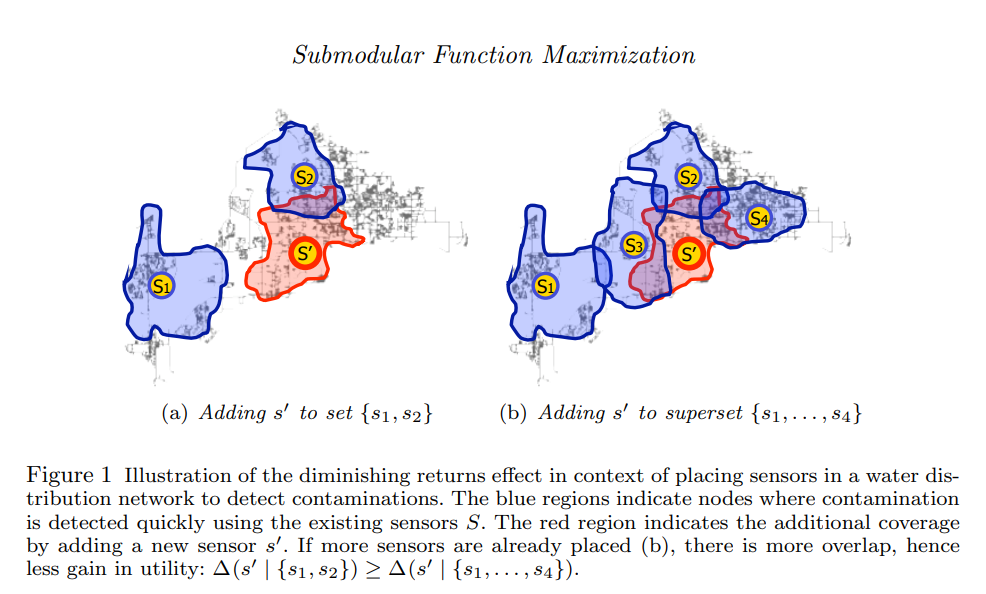
자 $A=\{ s_{1},s_{2}\}$ 이고 $B=\{ s_{1},s_{2},s_{3},s_{4}\} $ 인 상황이므로 B의 상황이 더 많은 센서가 설치되었다고 보시면 되고 그로 인해 수질오염을 검출할 수 있는 지역이 많은 상황입니다.
$A\subseteq B$인 상황에서 새로운 센서 S'를 설치하게 됐습니다.
A 같은 경우는 기존의 탐지 가능했던 지역이 적었기 때문에 새로운 센서 S'로 인해 새롭게 탐지 가능해진 지역이 비교적 큽니다.
B 같은 경우는 기존의 탐지 가능했던 지역이 어느 정도 있었는 데 새로 들어온 S'는 기존의 영역과 겹치는 부분이 커서 새롭게 탐지 가능해진 지역이 비교적 적습니다.
즉 , Set function의 input으로 들어오는 집합의 크기가 적었을 때 발생하는 이득(함수의 증분)이 더 크다는 것을 의미합니다.
공부를 처음 할 때 들어오는 지식의 양이랑 , 1 회독 2 회독을 거치고 난 후에 공부를 다시 할 때 들어오는 지식의 양이 차이가 나는 것을 상상해보시면 될 거 같습니다.
저 submodularity 함수를 최대화해야 하는 상황이 있고 , 최소화해야 하는 상황이 있는데 본 논문에서는 최대화하는 방향으로 진행이 됩니다. 결국 Video-Summarization을 하는 데에 중요하게 여겨지는 value(Representativeness , Uniqueness)들을 최대화하는 optimization이 진행되게 됩니다.
Submodular function을 어떻게 Maxmization을 하는지는 다양한 방법이 있지만 , 자세히 다루지는 않도록 하겠습니다.
Monotonic function
단조함수입니다. 미적분학에서 함수의 수렴성을 판단할 때 단조 증가함수 , 단조 감소 함수 이런 얘기를 들어보신 적이 있을 텐데 단순히 증가하거나 , 감소하는 함수로 생각하시면 됩니다.
- 임의의 $x,y\in I$ 일 때 , $ x\leqq y $ 라면 $f(x)\leqq f(y)$ 함수 $ f $를 단조 증가함수라고 정의해줍니다. 아래의 함수가 단조 증가함수(monotonically increasing function)입니다.
본 논문에서 중요하게 쓰이는 개념은 아니지만 한번 정리해봤습니다.
Proposed Framework
논문이 제안한 Framework에 대해서 이제 알아보도록 하겠습니다. 본 논문은 2015년도에 나온 논문이라 딥러닝이 태동하고 있던 시기에 나온 논문입니다. 따라서 여기서 제안하는 방법은 신경망 기반이 아닌 , 단순한 최적화 문제로 Video Summarization 문제를 해결하 고 있습니다. 그러면 위에서도 잠깐 소개했지만 Video Summarization을 진행하는 데에 있어 고려해야 할 가치에 대해서 알아보도록 하겠습니다.
Video Summarization이 잘 됐는지 판단은 어떻게 해야 할까요? 예를 들어 무언가를 요약할 때 우리가 노트 정리를 할 때를 보면
- 표현력이 좋아야 합니다. 즉 , summarization에 들어간 key-frame들은 원래 비디오에 포함된 event를 대표적으로 나타낼 수 있는 프레임으로 구성되어 있어야 합니다. 대충 key-frame만 봐도 이 비디오가 어떤 비디오구나 라는 것을 짐작할 수 있게 해야 한다는 의미입니다. 본 논문에서는 이 개념을 Representativeness로 표현하고 있습니다.
- 유일해야 합니다. 즉 , 중복이 없어야 된다는 소리입니다. 각 key-frame마다 unique 한 정보를 표현함으로 써 , 최대한 중복이 없게 끔 담아주는 것 또한 중요합니다. 요약을 잘한다는 게 표현력도 중요하지만 얼마나 간략하게 표현하는 것도 중요하겠죠? 본 논문에서는 이 개념을 Uniqueness라고 표현하고 있습니다.
결국 , Video Summarization을 잘하기 위해서는 Representativeness와 Uniqueness를 Maximize 하는 방향으로 framework가 설계되어야 합니다. 그럼 이제 슬슬 본론으로 들어가 보도록 하겠습니다.
N개의 프레임을 가지고 있는 비디오를 다음의 집합으로 표현하겠습니다. $V=\{ v_{1},v_{2},\cdots ,v_{n}\}$ 이때 이를 Summarization 한 부분집합은 $S=\{ s_{1},s_{2},\cdots ,s_{m}\} ,(m\leqq n)$ 이렇게 표현할 수 있겠습니다.

이때 Representativeness는 다음과 같이 계산해줍니다.
- $R(S)=\sum_{i\in V} \max_{j\in S} w_{ij}$ : Summarization에 속한 key-frame과 Original에 있는 모든 비디오 간의 Cosine Similarities를 계산해주고 각 최댓값만 가지고 와서 Summation 해줍니다. 이 $R(S)$를 최대화시키는 것은 Summarization이 원래 비디오와의 유사도를 증가시킨다고 보시면 되겠습니다.
그리고 Uniquness는 다음과 같이 계산해줍니다.
- $U(S)=\sum_{i\in S} \min_{j\in S,j<i} d_{ij}$ : Summarization에 속한 key-frame 간의 거리를 나타내며 우리는 key-frame들이 중복되는 정보를 담고 싶지 않은 상황이므로 frame간의 거리를 최대화시키고 싶은 상황입니다. 그래서 저 수식의 의미는 key-frame 간의 거리를 모두 계산해주고 그 최솟값들만 가져와서 Summation 해줍니다. 그러고 나서 $U(S)$를 최대화하는 것은 frame끼리의 최소거리를 넓혀주는 방향이니 서로서로 멀리 떨어지게끔 해주는 것을 의미합니다. 이때 거리는 Chi-Square distance로 두 frame끼리의 color histogram 차이를 사용한다고 합니다.
그럼 저 두 가지를 선형 결합한 목적 함수인 $Q(S)=R(S)+\lambda_{1} U(S)$를 정의할 수 있는 데 한 가지 문제가 생깁니다. R(S)를 최대화하는 가장 간단한 방법은 모든 프레임을 key-frame으로 선택하는 방법이 있습니다. 따라서 Summarization 집합의 크기에 비례해서 penalty를 부여하게 됩니다.
- objective function : $Q(S)=R(S)+\lambda_{1} U(S)+\lambda_{2} \mid V-S\mid $
논문에서 밝히는 다음 과정은 위에서 정의한 목적함수가 일단 Submodular Function이라는 것을 밝히는 증명을 거치게 됩니다. (증명 과정을 이해하는 것은 필수가 아닙니다.)
Theorem 1. The objective function Q(S) is submodular
- $ Q(S) =\sum_{i\in V} \max_{j\in S} w_{ij}+\lambda_{1} \sum_{i\in S} \min_{j\in S,j<i} d_{i,j}+\lambda_{2} \mid V-S\mid $
이때 , $ x\in V-S $인 원소를 가지고 다음의 관계식을 얻을 수 있습니다.
- $ Q(S\cup \{ x\} )-Q(S)=\sum_{i\in V} max\{ 0,w_{ix}-\max_{j\in S} w_{ij}\} +\lambda_{1} \min_{i\in S} d_{ix}-\lambda_{2} $
그리고 임의의 두 summary set $ S_{1}\subseteq S_{2} $을 고려해보면 다음의 부등식이 성립한다고 합니다. 근데 조금 의문이 드는 게 아래의 부등식이 성립하기 위해서는 w라는 값이 무조건 양수 일 때만 가능한 조건인데 저 w는 cosine similarity로 [-1,1]의 범위를 가지는 데 어떻게 성립한다는 것인지 조금 의아합니다.
- $ \max_{j\in S_{1}} w_{ij}\leqq \max_{j\in S_{2}} w_{ij} $
이를 이용하여 다음의 부등식을 정의할 수 있습니다.
- $ \sum_{i\in V} max\{ w_{ix}-\max_{j\in S_{2}} w_{ij}\} \leqq \sum_{i\in V} max\{ w_{ix}-\max_{j\in S_{1}} w_{ij}\} $
어느 Subset에 대한 부등호 인지 잘 확인해주시길 바랍니다. 또한 distance에 대해서도 부등식을 얻을 수 있는데
- $ \min_{i\in S_{2}} d_{ix}\leqq \min_{i\in S_{1}} d_{ix} $
이를 정리하면 $ Q(S_{2}\cup \{ x\} )-Q(S_{2})\leqq Q(S_{1}\cup \{ x\} )-Q(S_{1}) $가 성립하고 이를 통해 Q(S)가 submodular function이라는 것을 알 수 있습니다.
우리가 정의한 목적함수가 Submodular function이라는 것을 알았고 우리는 저 목적함수를 최대화시키는 것이 목적이니깐 결국 Submodular function maximization 문제가 됩니다.

Submodular function을 최대화하는 방법은 정말 다양하게 있습니다. 위의 알고리즘은 Unconstrained 상황에서 Submodular function을 최대화하는 알고리즘입니다. 저기서 $u_{i}$는 원래 비디오 프레임의 순서를 무작위로 섞은 것입니다.
- 초기 조건(Initialization) : $X$는 공집합으로 , $Y$는 original video 집합으로 초기화해줍니다. 결국 저 X라는 집합에 Summarization이 , key-frame들이 추가된다고 보시면 됩니다.
- 종료 조건(Termination) : Iteration이 N번 반복되면 종료됩니다. 따라서 알고리즘의 Time-Complexity는 $ O(N) $입니다.
각각의 Iteration을 돌면서 Input 집합에 대한 Set Function의 증분을 가지고 확률을 계산합니다.
- $ a_{i}=f(X_{i-1}\cup u_{i})-f(X_{i-1}) $
- $ b_{i}=f(Y_{i-1}-u_{i})-f(Y_{i-1}) $
- $ a^{\prime }_{i}=max\{ a_{i},0\} ,b^{\prime }_{i}=max\{ b_{i},0\} $
- $ \frac{a^{\prime }_{i}}{a^{\prime }_{i}+b^{\prime }_{i}} $의 확률로 $X_{i}=X_{i-1}\cup \{ u_{i}\} ,Y_{i}=Y_{i-1}$를 적용해줘서 집합 $X$에 $u_{i}$를 추가해줍니다.
- $ \frac{b^{\prime }_{i}}{a^{\prime }_{i}+b^{\prime }_{i}} $의 확률로 $X_{i}=X_{i-1},Y_{i}=Y_{i-1}-u_{i}$를 적용해줘서 집합 $Y$에서 $u_{i}$를 제거해줍니다.
이렇게 submodular function의 증분을 가지고 X에 집합을 추가하거나 , Y에 집합을 제거하는 Iteration을 돌리고 나면 X에는 submodularity를 최대화시키는 방향으로 진행된 집합들(key-frame)들이 남아나게 됩니다.
이 최적화 알고리즘은 이 정도로만 설명을 하고 더 깊은 이해를 하고 싶으신 분들은 따로 Submodular function optimization을 찾아보시길 바랍니다.
Experiments
실험 부분입니다. Baseline으로 선택한 방법론은 1) Uniform Sampling , 2) Clustering , 3) Video Precis로 세 가지입니다. 모두 Static 하게 Summarization의 크기를 사전에 정의를 해줘야 하는 방법론입니다.
평가는 어떻게 하냐면 Summarization을 바탕으로 reconstruction을 할 때 reconstruction error가 일정 threshold를 넘어서는 frame의 개수를 바탕으로 진행이 됩니다. 즉 , 문제를 일으키는 frame의 개수가 적을수록 성능이 좋다고 얘기하고 있습니다. 사실 여기서 reconstruction이 어떻게 진행되는지 까지는 나와있지 않았습니다.
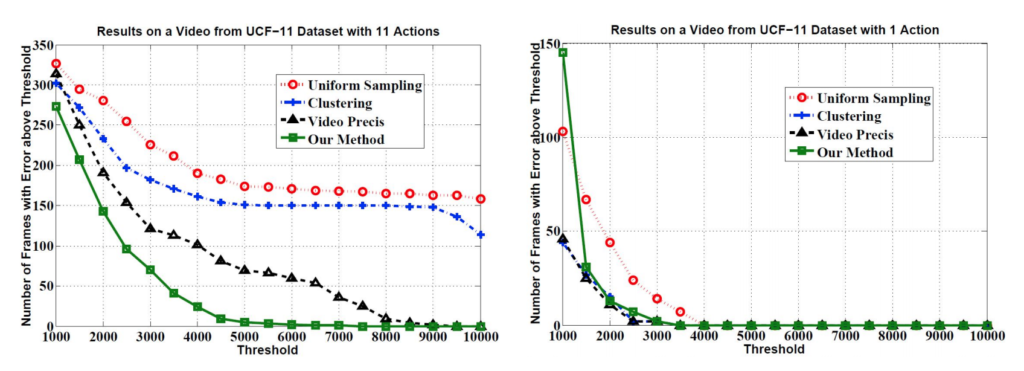
Action Recognition 진영에서 활용되던 UCF-101 데이터셋을 가지고 만들어낸 평가 그래프입니다.
x 축이 Reconstruction error의 threshold입니다. y 축은 Threshold를 넘긴 frame의 개수로 y축의 값이 적을수록 Summarization의 성능이 높게 나왔다고 얘기하고 있습니다. 본 논문에서 제안된 Framework가 가장 낮은 y 값을 가지고 있고 , Threshold가 증가함에 따라 에러를 일으키는 프레임의 개수가 빠르게 감소하는 양상을 보여주고 있습니다.
사실 저는 이 metric이 과연 정말 Summarization에 적합한 평가지표인지는 의문이 들지만 , 15년도에 나온 논문이라는 점을 감안한다면 아직 정립이 제대로 안됐을 테니 저랬을 수도 있었을 것 같습니다.
암튼 Static Summarization에 비해 더 좋은 정량적 성능을 보여주고 있었습니다.
- Qualitative results

정성적 평가입니다. 총 11개의 action을 담는 비디오를 가지고 Summarization을 진행했을 때 , 가장 아래에 있는 본 논문에서 제안된 방법론이 중첩되는 프레임이 없이 대표적인 frame으로 잘 요약을 한 것을 볼 수 있습니다. 다른 방법론을 보면 중첩도 많고 어떤 action인지 잘 구분하기 힘든 프레임도 좀 섞여있는 거 같습니다.
Conclusion
사실 key-frame selection에 대한 서베이를 진행하면서 최근의 딥러닝 기반 비지도 학습 방법론들은 GAN을 사용하거나 강화 학습을 이용하는 방법이 대부분이었습니다. 딥러닝 기반의 방법론들에 대한 본격적인 서베이를 진행하기 전에 간단하게 Optimization-based framework를 살펴보았고 Dynamic 한 key-frame selection이 static 한 key-frame selection에 비해서 더 표현력이 좋다는 사실을 알 수 있었습니다.
요즘의 Video Summarization은 사실 거의 Action 쪽에 치우쳐져 있습니다. 근데 본 논문에서 제안된 framework는 비디오 데이터셋의 특성에 구애받는 방법론은 아닌 거 같습니다. 지금 계획으로는 이 알고리즘을 빠르게 구현해봐서 CDVA framework에서 사용되는 color histogram 기반의 방법론과 비교를 해보려고 합니다.
리뷰 읽어주셔서 감사합니다.



