Before Review
오늘 준비한 논문은 비디오 논문이 아닌 다른 논문을 가져왔습니다. Student-Teacher 기반의 semi 혹은 self supervised 방법론에 적용할 수 있는 새로운 Normalization을 다룬 논문입니다.
Simple is Best라고, 방법론 자체는 굉장히 간단합니다. 간단한 만큼 적용하기 쉬우며 좋은 성능과 범용성을 보여주기 때문에 CVPR에 accept 된 것 같습니다.
혹시 본인이 지금 연구하거나, 연구할 방향이 Student-Teacher 기반의 Semi, Self Supervised 방법론이라면 본 논문에서 제안되는 Normalization 기법을 사용해보는 것도 나쁘지 않을 것 같습니다.
리뷰 시작하도록 하겠습니다.
Preliminaries
논문의 얘기를 시작하기에 앞서 알아야 하는 지식들이 있습니다.
Batch-Normalization
각 Layer로 들어가는 Batch 단위의 Input들의 통계치를 계산해주고 이를 이용해 Batch 안에 있는 data들을 정규화시켜주는 기법입니다.

그리고 정규화가 진행된 다음에 scaling과 shift가 진행이 되는 데 저 $\gamma$ , $\beta$는 같이 학습이 되는 parameter입니다. BatchNorm을 써주면 수렴 속도가 빨라지고 , 성능이 좋아지는 등 학습 전반적인 과정에 안정성을 가져다줍니다.
Exponential Moving Average
쉽게 얘기하면 오래된 데이터에 대한 가중치는 지수적으로 감소하지만 0이 되지는 않게 끔 계산하는 방법입니다. 오래된 데이터라는 얘기를 보아하니 시간의 개념이 들어가는 것 같습니다. 평균은 동일 시점에서 산출이 되는 것이지만 , 이동 평균은 동일 대상이지만 시점이 서로 상이해서 발생합니다. 예를 들어 운동시간에 따른 피로도 누적을 단순한 평균으로 계산하면 문제가 발생합니다.
10일 전에 했던 운동시간과 어제 했던 운동시간이 피로도 누적 측면에서 동일한 가중치를 가질까요? 그렇지 않습니다. 이럴 때 사용되는 개념이 지수 이동평균(EMA)입니다. 최근에 발생한 일에 대해서는 높은 가중치를 주고 , 시간이 지나간 일에 대해서는 낮은 가중치를 주지만 영향력을 그래도 고려하는 방법입니다.
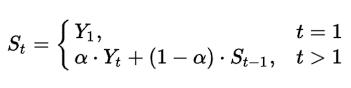
수식은 위와 같습니다. 저기 $\alpha$ 값을 거의 0.999로 사용을 해주는 데 이러면 과거의 데이터는 그 영향력이 지수적으로 감소하게 되겠죠?
바로 뒤에서 알아보겠지만 이 EMA를 가지고 Teacher Network의 Parameter를 계산해줍니다. 이게 어떤 의미를 가지는지는 Mean-Teacher Framework를 알아보면서 확인하겠습니다.
Mean-Teacher Framework
Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results
The recently proposed Temporal Ensembling has achieved state-of-the-art results in several semi-supervised learning benchmarks. It maintains an exponential moving average of label predictions on each training example, and penalizes predictions that are inc
arxiv.org
위의 논문에서 제안된 방법론으로 Semi-Supervised 기반의 방법론입니다. 당시 SOTA 였던 Temporal Ensemble 기반의 Semi-Supervised 방법론의 성능을 뛰어넘는 framework를 제안한 논문입니다.

Mean teacher framework는 위의 사진과 같습니다. 두 개의 model이 존재하는 데 , student와 teacher model은 같은 network 구조를 가집니다. 이때 , student model은 labeled data를 Input으로 받고 teacher model은 unlabeled data를 Input으로 받습니다.
결국 Student model은 annotation을 기반으로 supervised 방식의 학습 과정을 거칩니다. 즉 , Gradient 기반으로 parameter가 update 된다는 소리입니다. Student가 만들어내는 Output은 위의 그림으로는 classification cost라 적혀있지만 그냥 Supervised Loss라고 생각하며 됩니다.
그렇다면 Teacher model의 parameter는 어떻게 update 될까요? teacher model은 unlabeled data를 처리하기 때문에 Supervised 방식으로 parameter를 update 할 수 없습니다. 여기서 teacher model은 student model의 parameter를 지수 이동 평균(EMA)하여 parameter를 update 합니다.
따라서 Teacher model에서는 parameter의 update가 단순히 student model의 parameter를 평균 내주는 방식으로 처리하기 때문에 backpropagation이 진행되지 않습니다.
Teacher model이 EMA 방식으로 student의 parameter를 받아오기 때문에 이는 student의 시간의 변화에 따른 checkpoint를 부드럽게 ensemble을 하여 student model의 일반성을 체득할 수 있다고 합니다.
이렇게 Teacher model도 unlabeled data를 받아와서 prediction을 할 수 있고 , student model이 만들어내는 prediction과 얼마나 일관성이 있는지 consistency Loss를 계산합니다.
최종적으로 Student model은 Supervised Loss + Consistency Loss를 가지고 parameter를 update 시키면서 위의 과정이 반복이 되는 구조입니다.
Introduction
Large scale의 데이터셋 덕분에 예를 들면 ImageNet , MS-COCO 그리고 ShapeNet 등등 , Supervised 기반의 학습 방식은 다양한 Visual task에서 좋은 성능을 보여주고 있습니다. 하지만 대용량의 어노테이션이 된 데이터셋은 한정적입니다. 특히나 의료분야의 어노테이션 된 데이터셋은 구하기 힘든 상황입니다.
그렇기 때문에 사실 어토테이션된 데이터셋에 의존적인 Supervised Learning의 한계로 인해 Semi 혹은 Self-Supervised 로이 연구도 활발히 이루어지고 있습니다. 덕분에 특정 domain에서는 Supervised와 거의 비슷한 성능을 보여주는 연구도 나왔습니다.
Semi-Supervised 혹은 Self-Supervised에 사용되는 방법론은 다양하지만 그중 효과적인 것은 Student-Teacher model이라고 합니다. 여기서의 Student-Teacher의 관계는 Knowledge distillation의 느낌이랑은 살짝 다른 것 같습니다.
Knowledge distillation의 상황에선 미리 잘 학습된 더 큰 규모의 Network인 Teacher Network의 지식을 더 작은 규모의 Network인 Student Network가 잘 전달받아서 상대적으로는 적은 Parameter를 가지고 있지만 더 좋은 성능을 끌어내기 위해 사용이 됩니다.
Semi 혹은 Self Supervised에서 사용되는 Student-Teacher 방법론은 이러한 관계가 아니라 Unlabeled Data를 이용하기 위해 Teacher Network가 사용이 된다고 위에서 설명을 했었습니다. 이러한 차이를 알아주시길 바랍니다.
무튼 Semi 혹은 Self Supervised 진영에서의 Student-Teacher 방법론에서 기존 방법론들은 Batch-Normalization을 조금 변형시킨 Shuffle-BN 혹은 SyncBN을 사용했었습니다. 하지만 논문의 저자는 Student-Teacher 모델에 이렇게 BN을 단순히 적용시키는 것은 두 가지의 문제점을 야기시킨다고 합니다. 두 가지의 문제점이 무엇인지는 조금 뒤에서 다루는 것으로 하고 저자는 이 두 문제점을 해결할 수 있는 EMAN을 제안합니다.
아래의 그림을 한번 보도록 하겠습니다.
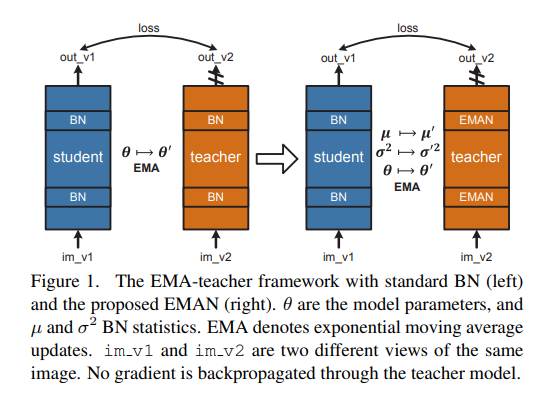
왼쪽의 그림이 BN 기반의 Mean teacher framework입니다. 단순히 model parameter들만 EMA 방식으로 전달해주고 Teacher model의 BN은 전달받은 parameter를 기반으로 통계치를 계산해 진행이 됩니다.
오른쪽 그림이 본 논문에서 제안하는 방식입니다. 정말 간단합니다. BN을 진행할 때 필요한 통계치들(평균 , 분산)들 역시 Student Network의 통계치들을 EMA 방식으로 계산해서 전달해주는 것입니다.
즉 원래는 모델의 Parameter만 EMA로 전달해주었는데 , Normalization에 필요한 통계치들 역시 EMA로 전달해준다는 것입니다. 그래서 이 EMA를 통해서 normalzation을 해주는 것을 EMAN이라고 본 논문에서는 표현이 되고 있습니다.
뒤에 Experiments를 통해 알아보겠지만 , 이 EMA-Normalization을 Semi , Self Supervised 기반의 방법론에 적용했을 때 , 방법론 , Network 구조 , 학습 시간 , 데이터셋에 관계없이 모두 좋은 성능을 보여주고 있기 때문에 EMAN 자체가 강한 Contribution이 되는 것 같습니다.
Exponential Moving Average Normalization
기존의 Mean teacher framework는 학습 과정에서 Standard Batch Normalization을 사용했었습니다.
- student : $y=f(BN(x), \theta )$
- teacher : $y'=f(BN(x), \theta' )$
f는 relu-conv와 같은 layer를 의미합니다. standard BN은 SGD 기반으로 update 되는 student model에는 잘 작동하였습니다. 하지만 EMA 방식으로 parameter들이 update 되는 teacher model에는 더 이상 잘 작동하지 않습니다. 저자는 그 이유를 다음과 같이 두 가지로 밝히고 있습니다.
- Cross Sample Dependency
자 , Student-Teacher model을 사용했던 이유는 unlabeled data를 사용하기 위함이었습니다. 좀 더 자세히 얘기를 해보자면 Teacher model을 활용하여 unlabeled data를 처리하고 이를 활용해 student model을 consistency Loss를 활용해서 좀 더 똑똑하게 만드는 것이 목적이었습니다.
즉 Teacher model이 일종의 pseudo ground-truth를 만들어내고 teacher와 student의 prediction을 비교함으로 써 어느 정도 student model을 지도를 한다는 의미입니다.
근데 Standard BN을 써버리면 data $x_{1}$에 대한 pseudo label이 다른 data에도 영향을 받아버리게 됩니다. 무슨 말이냐면 data $x_{1}$을 정규화하는 과정에서 batch 안에 있던 다른 data들을 이용해 구한 평균과 분산을 사용하였으니 , $x_{2}, x_{3} \ldots , x_{n}$에 dependent 해집니다.
분명히 $x_{1}$에 대한 pseudo label은 다른 데이터에 대한 dependency가 높지 않아야 합니다. 이게 BN을 썼을 때 Teacher model에서 발생하는 문제점입니다.
- Parameter mismatch
다음 문제점은 Teacher model의 parameter인 $\theta'$와 batch-wise BN 통계치 ($\mu _{ \beta},\sigma _{ \beta }^2$) 간의 mismatch 문제입니다.
Teacher model의 parameter는 이전 iteration의 parameter로 EMA 되는 반면 BN 통계치는 현재의 iteration 값으로 계산이 된다고 합니다. 이렇게 Teacher model의 parameter와 BN statistics에 반영되는 타이밍이 각각 다르다 보니 parameter space에서 non-smootheness를 야기시킨다고 합니다.
Parameter mismatch는 사실 정확히 이해를 못했습니다. 무튼 이러한 문제점이 존재한다고 저자는 주장하고 있고 이를 해결하기 위해 EMA-Normalization을 제안합니다. 이 EMA-Normalization은 Teacher model에서만 사용해주고 Student model은 그대로 BN 기반의 정규화를 진행해줍니다.
- $y'=f(EMAN(x), \theta' )$
- $\hat{x}=EMAN(x)= \gamma \frac{x- \mu '}{ \sqrt{\sigma '^2+ \epsilon} } + \beta$
- $\mu '=m \mu '+(1-m) \mu$
- $\sigma'^{2}=m \sigma'^{2}+(1-m)\sigma^{2}$
이제 Teacher model에 들어가는 input들을 정규화하는 데 있어서 각 input들은 서로 indepedent 해집니다. 그 정규화를 하는 데 있어 사용되는 통계치들은 Student model에서 건너온 통계치만 사용하기 때문입니다. 즉 , Cross-Sample Dependency가 해소됩니다. parameter mismatch도 해결이 된다고 하는 데 , 정확히 이해되지는 않습니다..

의사 코드입니다. 첫 번째 루프를 보면 student model의 parameter를 불러와서 EMA 방식으로 teacher의 parameter를 계산해주고 있습니다.
두 번째 루프는 statistics를 EMA로 계산해주고 있습니다. EMA-Normalization을 위함이라 보시면 됩니다.
Experiments
본 논문에서는 Image 분야에서 Semi-Supervised 기반에서 SOTA인 FixMatch와 Self-Supervised에서 SOTA를 보여주는 MoCo , BYOL에 EMA-Normalization을 적용했을 때의 성능을 분석하고 있습니다.
- The Effect on EMAN

student와 teacher에 다양한 normalization 기법을 실험했을 때 성능입니다. 세 가지 방법론 모두 student는 BN , teacher는 EMAN로 했을 때 제일 높은 성능을 보여주고 있습니다. 방법론에 관계없이 모두 좋은 성능을 보여준다는 점은 인상 깊은 결과인 것 같습니다.
- Self-Supervised Evaluation
논문에서 베이스 라인으로 정의한 MoCo와 BYOL에 EMAN을 적용한 결과와 다른 Self-Supervised 방법론들과 성능을 비교한 실험입니다.
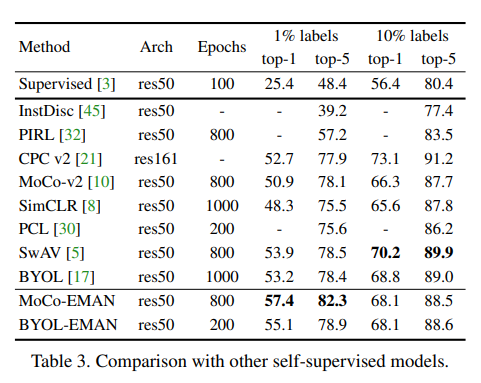
여기서 SwAV라는 방법론이 10% 일 때 , 제일 높은 성능을 보여주는 데 이는 SwAV라는 방법론의 Multi-crop이라는 기법에 기인한 결과라고 합니다. SwAV의 Multi-crop 기법은 데이터 전처리 기법 중 하나인데 , Computation Cost가 많이 든다는 단점이 있습니다.
- Semi-Supervised Evaluation
Semi Supervised 방법론이 FixMatch에 EMAN을 적용한 결과와 다른 Semi-Supervised 방법론들과 비교를 하고 있습니다. 우선 , 아래의 테이블에 있는 방법론들과 비교했을 때는 SOTA 성능을 보여주고 있습니다.

흥미로운 것은 21년도 CVPR에 나와서 본 논문에는 비교하고 있지 않지만 현재 SOTA의 성능을 보여주는 Meta Pseudo Labels이라는 방법론이 있습니다.
Meta Pseudo Label은 ImageNet-10% 일 때 Top1 : 73.89 , Top 5 : 91.38의 성능을 보여줍니다. FixMatch-EMAN과 거의 비슷합니다.
이 Meta Pseudo Label도 결국 Student-Teacher 기반의 방법론이라 , 본 논문에서 나온 Normalization을 적용했다면 어떻게 될까 라는 호기심이 생기긴 합니다.
Conclusion
본 논문을 봤을 때 느낀 건 간단한 아이디어 만으로 좋은 방법론을 만들어낸 연구에 많은 자극을 받았습니다.
제가 지난번에 리뷰했던 Temporal Action Proposal 논문인 SSTAP에 적용할 수 있을 거 같아서 현재 진행하고 있는 연구를 나중에 발전시킨 다면 SSTAP로 베이스라인 잡아보고 본 논문에서 제안된 Normalization을 적용해볼 수 있을 거 같습니다.
Student Teacher 기반의 framework를 현재 주제로 잡고 있다면 본 논문에서 제안된 EMA-Normalization을 적용해보는 것도 나쁘지 않을 거 같습니다.
리뷰 읽어주셔서 감사합니다!
'Paper Review > Computer Vision' 카테고리의 다른 글
| [ICCV 2023] ProbVLM : Probabilistic Adapter for Frozen Vision-Language Models (2) | 2024.01.15 |
|---|---|
| [ICLR 2022] How Do Vision Transformer Work? (1) | 2024.01.15 |
| [ICML 2021] An Image is Worth 16x16 Words : Transformer for image recognition at scale (1) | 2024.01.15 |
| [CVPR 2022] Masked Autoencoders Are Scalable Vision Learners (1) | 2023.01.12 |
| [ICCV 2017] Focal Loss for Dense Object Detection (0) | 2021.06.28 |



