Before Review
이번 논문 리뷰는 ViT에 대해 좀 더 깊은 분석을 진행한 논문을 읽었습니다.
흔히 알려져 있는 ViT에 대한 주장들에 대한 분석, ViT가 어떻게 작동하는지 이런 것들은 좀 더 면밀하게 분석한 논문입니다.
리뷰 시작하도록 하겠습니다.
Preliminaries
이번 논문에는 특히 수학적인 용어들이 많이 나옵니다. 저도 애매하게 알고 있던 부분들을 이번에 다시 한번 정리를 하였습니다. 내용이 조금 많으니 확인하시고 본인에게 필요한 부분만 참고하시면 될 것 같습니다.
제가 수학 관련 내용을 참조할 때 자주 방문하는 블로그가 있습니다.
아래의 그림이나 내용들은 모두 블로그의 내용을 참조하고 정리하였습니다.
Eigen-Value & Eigen-Vector
고윳값, 고유 벡터는 선형대수학에서 굉장히 중요하게 다뤄지는 주제입니다. 당장 기계 학습에서 배우는 주성분 분석(PCA)의 근간이 되는 이론이기도 하지요. 고윳값에 대한 얘기를 시작하려면 선형 변환부터 얘기를 해야 합니다.
벡터 $ x $에 행렬 $ A $를 곱하면 새로운 벡터 $ Ax $가 나오게 됩니다. 이때 보통은 벡터 $ x $와 새로운 벡터 $ Ax $의 크기와 방향은 달라지게 됩니다. 아래의 그림처럼 말이죠.
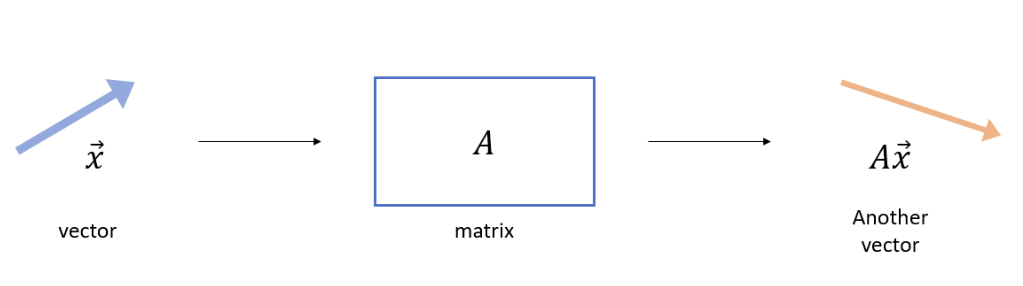
그런데 행렬 $ A $를 곱해도 방향이 변하지 않는 벡터가 존재합니다. 방향은 그대로 유지가 되며, 크기만 상수배가 되는 경우가 있죠. 바로 고유 벡터(eigen-vector)입니다.
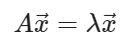
이때의 벡터 $\vec {x}$를 고유 벡터(eigen-vector)라 정의하고 그 스칼라 값 $\lambda $를 고윳값(eigen-value)라 정의합니다. 행렬 $ A $가 정방행렬일 때 고유벡터의 정의가 가능하며 $ A $가 0인 고윳값이 없으면 항상 역행렬이 존재합니다.
다시 얘기하지만, 벡터 $ x $에 행렬 $ A $를 곱하면 새로운 벡터 $ Ax $가 나오게 됩니다. 벡터 $ Ax $를 해석할 때는 그 벡터가 정의되는 벡터 공간을 살펴봐야 합니다. 그런데 이 선형 변환이 만들어내는 $ Ax $는 고유 벡터들의 선형결합만을 가지고도 굉장히 쉽게 해석이 가능해집니다.
즉, $ A $라는 행렬이 만들어내는 선형 변환은 $ A $라는 행렬이 만들어내는 고유 공간에서의 기저벡터로 해석이 가능합니다.
기존의 벡터 $ x $는 일단 직교 좌표계에서 정의가 될 수 있겠죠. 그런데 $ A $라는 행렬이 곱해지면 $ Ax $라는 벡터가 정의되는 좌표계가 아래와 같이 달라집니다.
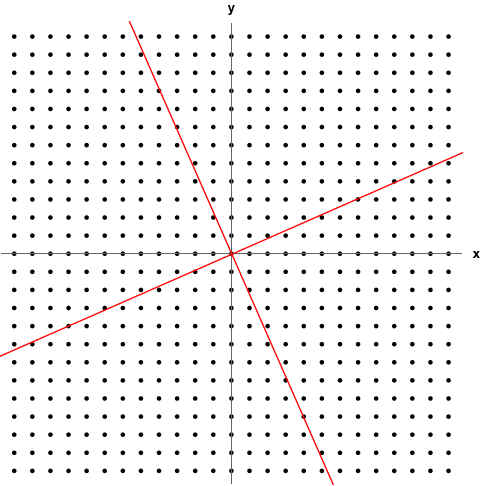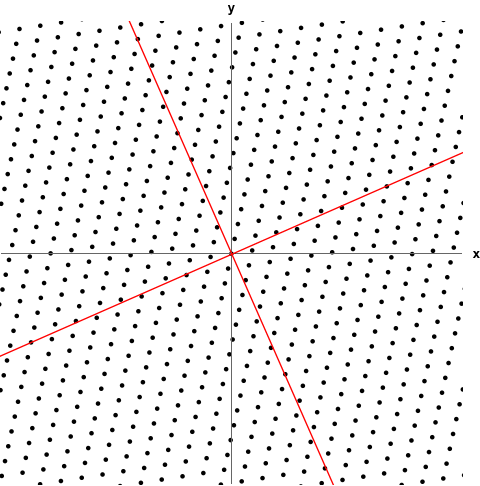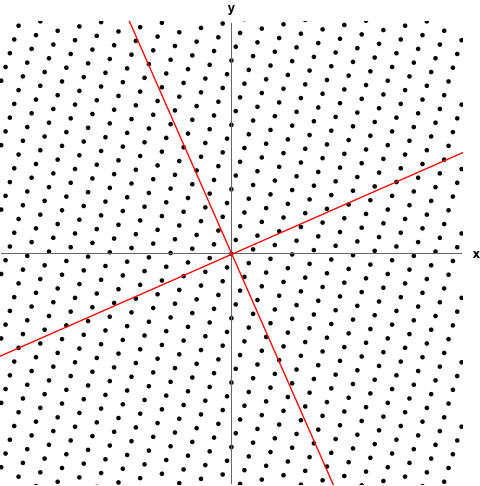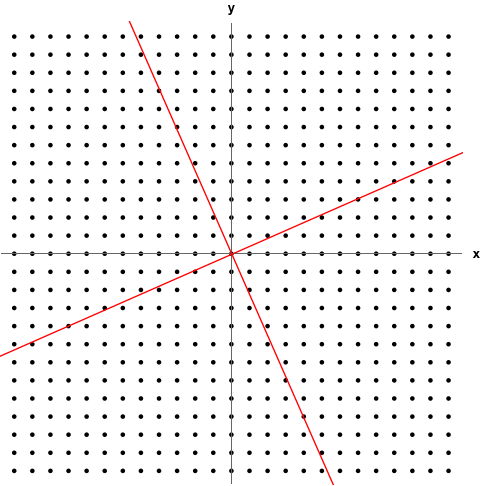
벡터가 정의되는 공간이 변하는 것인데, 고유벡터는 $ A $를 곱해도 방향이 변하지 않는 벡터라고 했습니다. 따라서 변하는 공간에 대해서 기저벡터의 역할을 하게 되는 것이죠.
정리하겠습니다.
- 고윳값, 고유벡터를 알면 행렬 $ A $가 만들어내는 선형 변환을 더욱 쉽게 이해할 수 있습니다.
Hessian Matrix
입력 값으로 독립 변수를 두 개 이상 가지면서 출력을 스칼라 값을 내뱉는 함수를 다변수 실함수 혹은 스칼라 장이라고 표현합니다. Hessian Matrix는 기본적으로 독립 변수를 두 개 이상 가지는 다변수 함수의 2계 미분을 나타내는 행렬이라 보시면 됩니다. 아래와 같이 $ n $ 개의 독립 변수를 가지는 실함수 $ f(x_{1},\cdots , x_{n})$에 대해 Hessian Matrix는 다음과 같습니다.

Hessian Matrix의 원소는 모두 이계도함수로 구성되어 있습니다. 함수 $ f $의 이계도함수가 연속이라면 클레로 정리에 의해 $\frac {\partial ^{2} f}{\partial x_{1} \partial x_{2}} = \frac {\partial ^{2} f}{\partial x_{2} \partial x_{1}}$를 만족합니다. 따라서 Hessian Matrix는 대칭 행렬(Symmetric Matrix)이 되는 것이죠.
Hessian Matrix이 가지는 성질과 의미는 많지만 여기서는 함수의 볼록성(Convexity)과 관련하여 얘기하도록 하겠습니다.
Hessian Matrix는 기본적으로 함수의 볼록성(Convexity)과 관련이 있습니다.
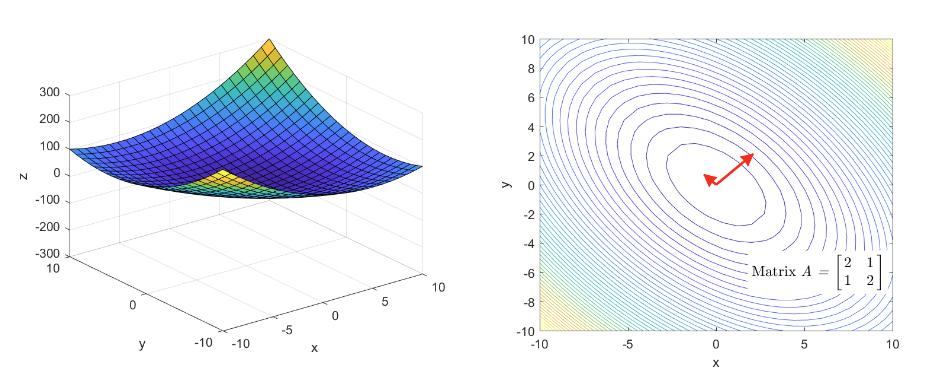
간단하게 생각해 보면 우리가 고등학교 때 배운 내용으로는 함수가 아래로 볼록하기 위해서
- $0\leq f^{\prime \prime }(x)$
라는 조건이 필요했습니다. 이계도함수가 항상 양수라는 것은 도함수는 단조 증가한다는 의미입니다. 도함수가 단조 증가하기 위해서는 아래의 그림과 같은 그래프의 모양이어야 합니다. 접선의 기울기가 계속 증가해야 하는 함수의 형태라는 뜻이죠.
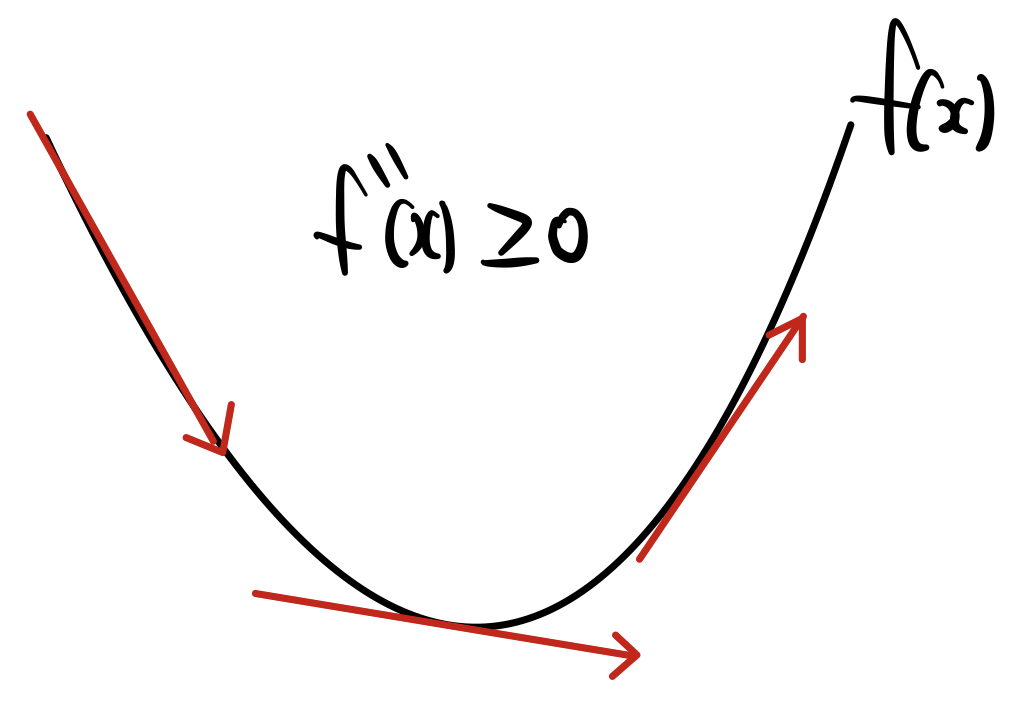
다변수 함수의 이차 미분은 Hessian Matrix를 통해 얻을 수 있을 것입니다.
- $0\preceq \nabla^{2} f(x)$
즉, Hessian Matrix가 양의 준-정부호 행렬이라면, 다변수 함수는 아래로 볼록 즉, convex function이 됩니다. 어떤 임의의 행렬이 양의 준-정부호임을 판단하기 위해서는 고윳값의 부호를 확인하면 됩니다.
Hessian Matrix의 고윳값이 모두 0 이상의 양수라면 Hessian Matrix는 양의 준-정부호 행렬이고 이는 원래의 다변수 함수 $ f(x_{1},\cdots , x_{n})$가 아래로 볼록 인 convex-function이라는 것입니다.
이때 고윳값은 여러 개가 나올 수 있는데 그중, 절댓값이 큰 방향으로 함수가 더욱 볼록해지는 성질이 있습니다. 즉, 고윳값이 양수이고 클수록 해당 고유 벡터 방향으로 함수는 더욱 아래로 볼록한(위로 급하게 접히는) 형태를 가지는 것이죠.
정리하겠습니다.
- Hessian Matrix의 고윳값이 모두 양수라면 다변수 함수(손실 함수)는 convex function의 형태를 가진다.
- Hessian Matrix의 고윳값의 절댓값이 클수록 다변수 함수는 그 고유벡터 방향으로 더욱 볼록한 형태를 가진다.
Convex Function
함수의 정의역이 convex set이며, 아래의 부등식을 만족하는 함수를 우리는 convex function이라 정의합니다.
- $ f(\theta x+(1-\theta ) y)\leq \theta f(x)+(1-\theta ) f(y),0\leq \theta \leq 1 $
여기서 등호가 사라지면 우리는 strictly convex function이라 정의합니다.
- $ f(\theta x+(1-\theta ) y)<\theta f(x)+(1-\theta ) f(y),0\leq \theta \leq 1 $

$\theta x+(1-\theta ) y $는 $ x $와 $ y $ 사이에 존재하는 정의역입니다. 거기에 대응되는 치역이 $ f(\theta x+(1-\theta ) y)$입니다.
$\theta f(x)+(1-\theta ) f(y)$는 $ f(x)$와 $ f(y)$의 line segment입니다. 그래프로 보면 $ f(x)$와 $ f(x)$를 이어주는 선분으로 보면 됩니다.
이때, 저 부등식이 의미하는 것은 함수의 두 point로부터 만들어지는 line segment는 항상 함수의 값보다 크거나 작다라는 의미입니다.
다음으로 convex function의 중요한 성질에 대해서 하나 얘기하도록 하겠습니다.
최적화 관점에서 함수의 최솟값을 찾는다고 가정했을 때, 목적 함수가 convex function이고 contraint가 없다면 optimal solution은 $\nabla f=0 $인 지점만 찾으면 끝입니다.
결국 최적화 입장에서 목적 함수가 convex function이라면 굉장히 문제 풀기가 쉬워진다는 뜻입니다. Constraint가 있다 해도 결국 convex function이라면 KKT 조건을 쓰든, 라그랑주 승수법을 쓰든 여러 가지 solver들이 있기 때문에 optimal solution을 거의 찾을 수 있습니다.
정리하겠습니다.
- 목적 함수가 convex function이라면 최적화 입장에서 문제가 굉장히 쉬워집니다.
Introduction
Transformer가 등장하고 그 핵심 연산인 multi-head self attention(MSA)은 computer vision에서 자주 등장하지만 왜 잘되는지 어떻게 작동하는지에 대해서는 이해가 부족했습니다. 사람들은 MSA가 잘 작동하는 이유에 대해서는 weak inductive bias와 long-range dependencies 덕분이라고 합니다.
하지만 한편으로 inductive bias가 작아서 즉, over flexibility 때문에 ViT는 작은 데이터에 대해서는 overfitting 하는 경향이 있다고 알려져 있습니다.
저자는 이렇게 ViT의 핵심이라 볼 수 있는 MSA에 대해서 좀 더 엄밀한 분석을 하며 ViT에 대한 기존의 주장들을 하나씩 점검하기 시작합니다. 저자가 확인하려는 것들은 아래와 같습니다.
"What properties of MSAs do we need to better optimize NNs?
Do the long-range dependencies of MSAs help NNs learn?"
신경망을 최적화시키는 데 MSA의 연산 중 어떤 특성이 도움이 되는 것인가? 이런 관점에서 정말로 long-range dependecy가 학습에 도움이 되는 것인가를 확인하기 위해 저자는 다양한 분석과 실험을 내놓습니다. 개인적으로 이 부분에서 등장하는 다양한 실험들이 인상 깊었습니다. Core-ML의 연구는 좀 더 수학적인 분석으로 주장을 내놓는 것이 인상 깊었네요.
"Do MSAs act like Convs? If not, how are they different?"
MSA가 Convs과 어떤 차이를 보이는지 저자는 주파수 관점에서 분석을 진행하였습니다. 결론만 말하면 MSA는 low-pass filter의 양상을 보이고 convolution은 high pass filter라는 것입니다. 이렇게 두 연산은 서로 반대의 양상을 보여줍니다. 하지만 둘을 적절히 잘 사용한다면 서로의 단점을 보완할 수 있다는 것도 저자의 생각입니다.
"How can we harmonize MSAs with Convs? Can we just leverage their advantages?"
저자는 multi-stage의 신경망이 각가 독립적인 small individual의 모델처럼 작동한다는 것을 밝힙니다. 뒤에 나오는 실험을 통해 stage를 지날 때마다 feature map의 variance가 높아지는 것을 확인할 수 있습니다. 따라서 저자는 MSA가 spatial smoothing 효과를 하기 때문에 variance를 낮출 수 있고 Convolution과 서로 상호보완적으로 작동할 수 있다고 주장합니다.
저자는 위의 의문들을 통해서 ViT가 정말로 어떻게 work 하는지에 대한 분석을 내놓습니다. 그럼 이제 각각의 질문에 대해서 좀 더 본격적으로 얘기해 보도록 하겠습니다.
What properties of MSAs do we need to improve optimization
The stronger the inductive biases, the stronger the representations

일반적으로 inductive bias가 약하면 small dataset에 대해서 쉽게 overfitting 된다는 얘기가 있습니다. 이러한 주장을 확인하기 위해 저자는 CIFAR-100에 대해서 train 데이터 셋과 test 데이터 셋에서의 양상을 비교합니다.
결국 overfitting이라는 것은 train에서 loss는 낮은데 test error가 높다는 것을 의미합니다. 위의 그래프에서 $ NLL_{train}$의 값은 작지만 $ Error $가 높은 것이 overfitting에 해당된다고 보시면 됩니다. 일단 CNN 계열은 $ NLL_{train}$의 값(train loss)도 작고 $ Error $(test error)도 작습니다.
하지만 ViT는 $ NLL_{train}$의 값(train loss)도 크고 $ Error $(test error)도 높습니다. 이건 overfitting이 아니라 그냥 학습을 잘 못하고 있는 것을 보여줍니다. CIFAR-100처럼 비교적 작은 데이터에 대해서 VIT는 overfitting이 아니라 학습을 잘 못하고 있었던 것입니다.
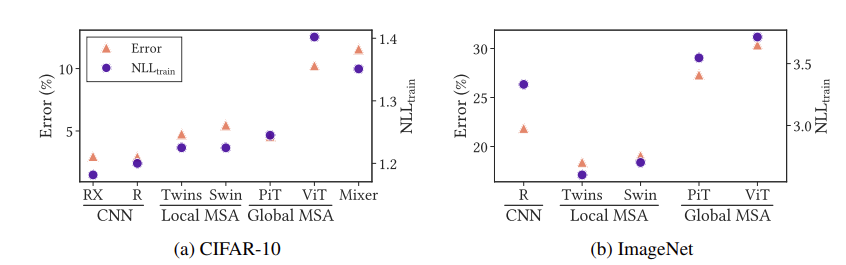
CIFAR-10이나 ImageNet에서도 동일한 경향성을 보여줍니다. 뒤에서 좀 더 다룰 예정이지만, inductive bias가 작은 ViT는 long-range dependency를 잘 해결한다고 알려져 있지만 이 역시 절대적인 것은 아닙니다. 결국 weak inductive bias가 좋은 feature representation을 보장해주지는 못하는 것이죠.
ViT does not overfit small training datasets
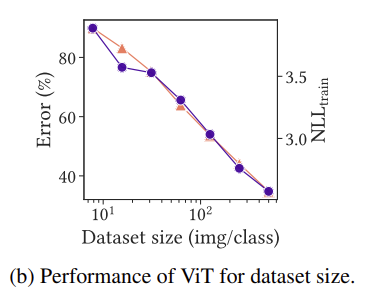
ViT는 small dataset에서 overfitting 되는 것이 아니라 학습을 못하는 것이라고 알아봤습니다. 하지만 데이터셋을 늘릴수록 train loss와 test error 둘 다 감소하는 모습을 볼 수 있네요. 이것을 통해 ViT의 poor performance는 overfitting이 아니라 small data regimes라는 것을 알 수 있습니다.
ViT's non-convex losses lead to poor performance
Loss landscape가 non-convex 하다면 학습이 당연히 어렵습니다. local minima나 saddle point에 수렴할 가능성이 높기 때문이죠. 저자는 ResNet과 ViT의 Loss landscape를 Hessian Matrix의 고윳값 관점으로 분석합니다.
- Hessian Matrix의 고윳값들이 대부분 양수라면 Loss 함수는 Convex의 성질이 높습니다.
- Hessian Matrix의 고윳값들이 양수와 음수 섞여 있다면 Loss 함수는 Non-Convex 합니다.
Hessian Matrix의 고유값들이 음수라는 게 중요한 게 아닙니다. 양수, 음수 섞여있으면 Loss함수가 non-convex라는 것이 중요한 것이죠. 그럼 음수만 있으면 어떻게 되는지 궁금할 수 있겠죠.
음수만 있으면 concave 형태가 되어 위로 볼록한 함수가 됩니다. 최댓값이 하나인 함수의 형태이죠. 이 역시 convex optimization problem이라 상관없습니다.
이런 관점에서 아래의 그래프를 한번 보시길 바랍니다.
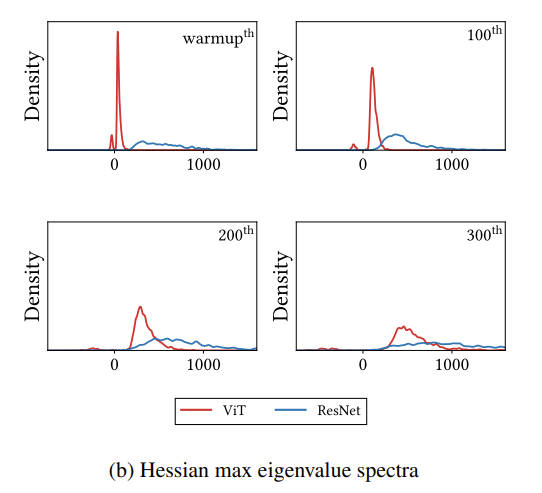
학습 초기에 ViT의 Hessian Matrix의 고윳값들은 0보다 작은 negative value들이 상당히 많습니다.
그에 반해 ResNet은 대부분 positive value로 이렇게 되면 loss의 convexity 증가하게 되죠. 또한 아래의 그래프를 보면 ViT를 모든 학습 데이터를 사용했을 때와 6%만을 가지고 학습했을 때의 차이를 보여주고 있습니다.
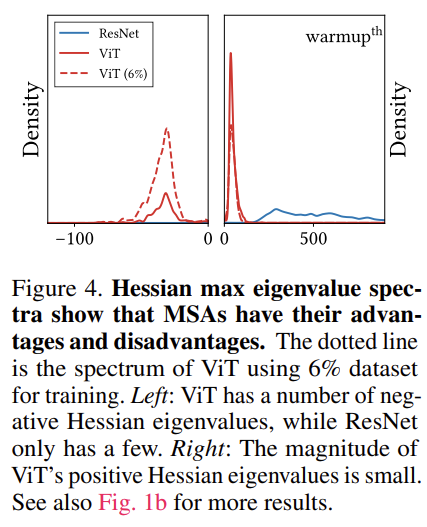
더 적은 6%의 데이터만을 가지고 학습을 하면 Hessian Matrix의 negative eigen value가 증가합니다.
이는 작은 데이터 셋에서 학습을 잘 못한다는 ViT의 원인이 이러한 non-convexity 때문이었다는 것을 알 수 있죠.
Loss landscape smoothing methods aids in ViT training
Loss landscape가 non-convex 하다는 것은 non-smooth인 함수와 비슷합니다.
이런 느낌인 것이죠. 물론 smooth 하다고 해서 무조건 convex라는 것은 아니지만, 신경망 학습에서 발생하는 non-convex lonss landscape는 non-smooth 한 성질도 보통 가집니다.
함수가 non-smooth 하면 문제가 되는 것이 gradient가 함수의 움직임을 예측하기 어렵다는 것입니다. 함수가 non-smooth 하다면 저렇게 튀어나온 첨점 부근에서는 gradient가 크게 발생하기 때문에 학습이 불안정해진다는 것이죠.
그래서 loss landscape를 smoothing 해주면 보통 학습이 안정화가 되며, 수렴 속도와 성능이 좋아지게 됩니다. 대표적으로 Batch-Norm을 예시로 들 수 있죠.
저자는 학습 초반에 ViT의 loss landscape가 non-convex function의 형태이기 때문에 smoothing 효과를 해주는 방법을 사용하면 ViT의 학습을 도울 수 있다고 합니다. 여기서는 Global Average Pooling(GAP)를 추가하여 비교합니다. 평균 연산은 대표적인 smoothing 연산이기 때문입니다.
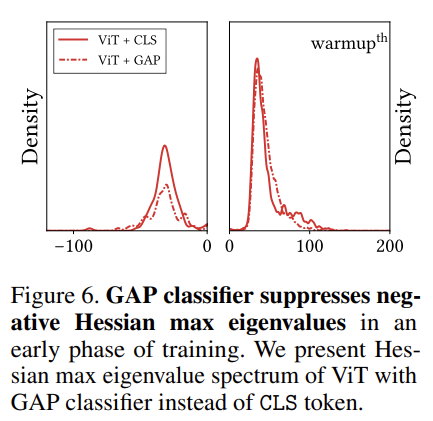
그래프를 보면 $ \text{ViT + GAP} $에 해당하는 점선을 보면 negative eigen value의 density가 줄어드는 것을 확인할 수 있습니다.
MSAs flatten the loss landscape
저자는 MSA가 Hessian eigenvalue의 magnitude를 감소시켜 주는 성질이 있다고 주장합니다.
위에서 본 그래프를 다시 한번 확인하면 확실히 ResNet에 비해서 magnitude 자체는 낮은 것을 확인할 수 있습니다. Y축은 density이고 x축이 magnitude라는 점 확인하시고 그래프를 보시길 바랍니다.
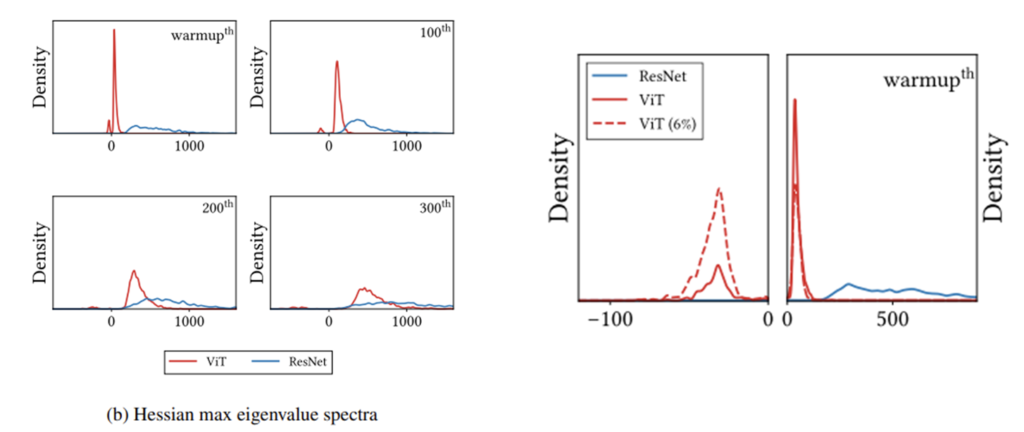
Hessian Matrix의 고윳값은 곡률(curvate)을 나타냅니다. 고윳값이 크다는 것은 고유벡터 방향으로 크게 휘었다는 말입니다. 고윳값이 대체적으로 작다는 것은 곡률이 작다는 것이고 loss 함수는 비교적 평평한 성질을 가지게 됩니다. 아래 그림처럼 말이죠.
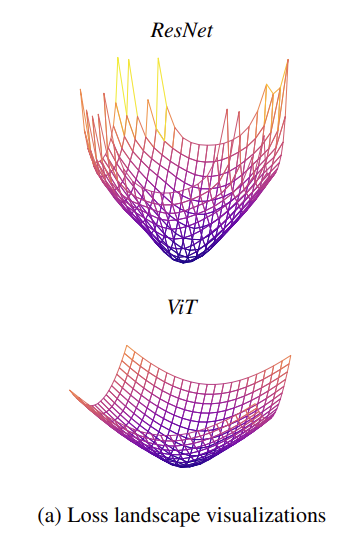
곡률이 너무 큰 것도 문제가 될 수 있습니다. 바로 gradient의 변동이 크기 때문이죠. 따라서 MSA는 large Hessian eignevalue들을 suppress 하여 신경망 학습에 도움을 줄 수 있습니다.
결국 large-scale data 도메인에서 ViT는 negative hessian eigenvalue의 영향을 덜 받으면서 loss 함수를 flatten 시키기 때문에 CNN에 비해 더 높은 성능을 보여주는 것이죠.
A key feature of MSAs is data specificity (not long-range dependency)
사람들이 MSA의 핵심은 long-range dependency라고 얘기들 합니다.
몇몇 논문들에서는 이러한 관점으로 이미 논문을 쓰고 있고요. 하지만 이러한 popular belief 와는 다르게 long-range dependency는 오히려 신경망의 optimization을 방해합니다.
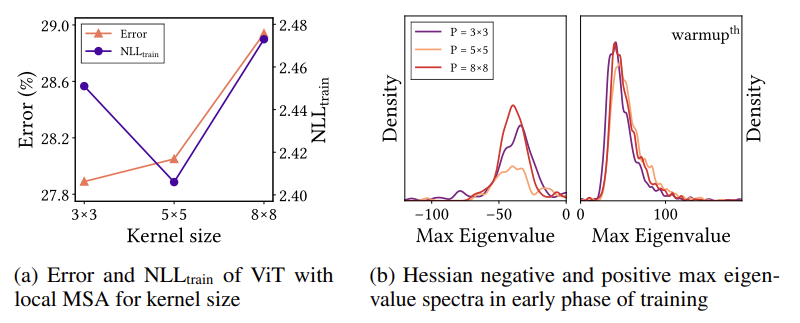
그래프를 보면 x축에 Kernel size라고 나와있습니다. Kernel size가 클수록 global attention을 수행했다고 보면 됩니다. 작을수록 local attention 이겠네요. 정말 long-range dependency가 학습에 도움이 되는 것이라면 kernel size가 클수록 더 좋은 양상을 보여야겠죠.
하지만 오히려 kernel size를 5x5로 했을 때 train loss, test error 둘 다 낮은 양상을 보여주고 있습니다. Negative Hessian eigen value 관점에서도 8x8 보다는 5x5가 더 많은 negative value를 suppress 해주고 있습니다.
따라서 중요한 건 long-range dependency가 아니라 그냥 "데이터마다 다르다."라고 얘기하고 있습니다.
ViT와 ResNet의 차이를 이렇게 loss landscape와 Hessian eigenvalue 관점에서 분석하였습니다. 이쪽 분야의 논문을 읽지 않아서 Core-ML 분야의 연구들이 어떠한 방식으로 분석을 진행하는지는 잘 모르겠지만, 처음 읽어보는 저의 입장에서는 굉장히 신선한 것 같습니다.
Do MSAs act like convs?
Convolution은 데이터와 상관없이 연산을 수행합니다. 그리고 채널마다 filter가 다르기 때문에 channel specific이라 볼 수 있죠.
MSA는 데이터에 따라 연산을 수행합니다. Self-Attention이 있기 때문이죠. 하지만 채널 같은 것은 고려되지 않습니다.
이러한 차이로 인해 Convolution과 MSA가 반대의 양상을 보여주게 됩니다. 반대의 양상이라는 것이 어떤 의미인지 확인해 보도록 하겠습니다.
MSAs are low-pass filter, but Convs are high-pass filters
우선 아래의 그림을 먼저 보면 ResNet과 ViT의 반대되는 양상을 확인할 수 있습니다. 저도 정확히 어떻게 진행한 것인지는 모르겠지만 feature map에 Fourier Transform을 가해 주파수 도메인에서 분석을 진행했다고 합니다.
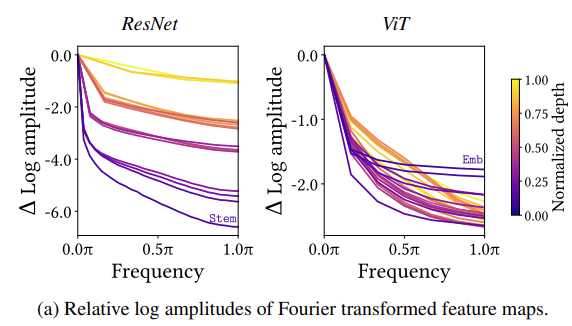
먼저 ResNet의 경우 레이어가 깊어질수록 고주파 성분이 커지지만, ViT의 경우 레이어가 깊어질수록 고주파 성분이 줄어드는 것을 확인하실 수 있습니다. 즉, Convolution은 고주파 성분을 통과시키는 high-pass filter의 역할을 한다고 볼 수 있지만 MSA는 저주파 성분을 통과시키는 low-pass filter의 역할을 한다고 볼 수 있습니다.
즉, MSA와 Convolution은 서로 다른 결과를 보여주는 연산입니다.
MSA는 attention weight를 통해 feature map을 aggregate 합니다. 약간 평균 내는 거랑 비슷하다고 볼 수 있죠. 따라서 MSA가 high frequency signal을 줄여준다는 것을 기대할 수 있습니다. 예외적으로 early layer에 있는 MSA는 이러한 양상이 아니라 반대의 양상을 보여준다고 합니다.
아래의 그림을 통해 확인해 보도록 하겠습니다.
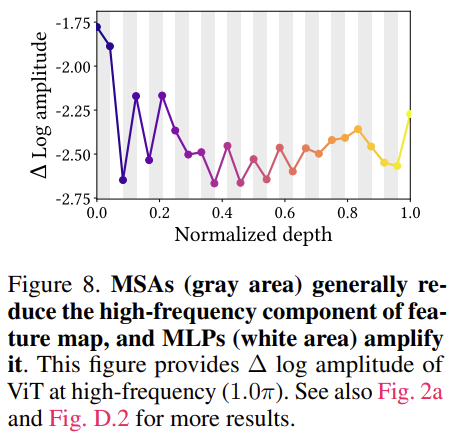
그래프의 회색 영역(gray area)은 MSA에 해당됩니다. 흰색 영역(white area)은 MLP를 의미합니다. Transformer Layer에 있는 MSA와 MLP를 의미한다고 보면 됩니다. X축은 depth로 layer의 깊이를 의미합니다.
Y축은 high frequency signal의 amplitude입니다. Early layer에서는 MSA가 high frequency의 amplitude를 높이고 있지만 deep layer에서는 high frequency의 amplitude를 낮추고 있습니다.
Convolution은 고주파 성분을 통과시키는 high-pass filter의 역할이고, MSA는 저주파 성분을 통과시키는 low-pass filter의 역할을 한다는 것을 아래의 그래프로도 확인할 수 있습니다.
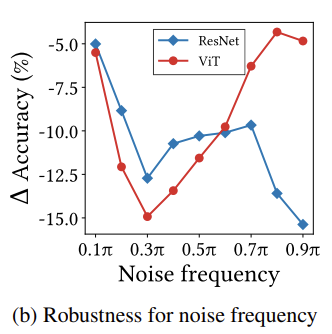
주파수에 따른 노이즈를 가했을 때 ViT는 저주파 노이즈에 취약한 모습을 보입니다. MSA는 저주파 성분을 통과시키는 low-pass filter이기 때문에 저주파 노이즈에 영향을 더 많이 받는 것이죠. ResNet은 정확히 그 반대의 양상을 보여줍니다.
MSAs aggregate feature maps, but Convs do not
MSA는 feature map을 aggregate 하기 때문에 feature map의 variance를 줄일 것이라고 기대할 수 있습니다.
이것을 확인하기 위해 저자는 feature map의 variance를 확인하였다고 합니다.
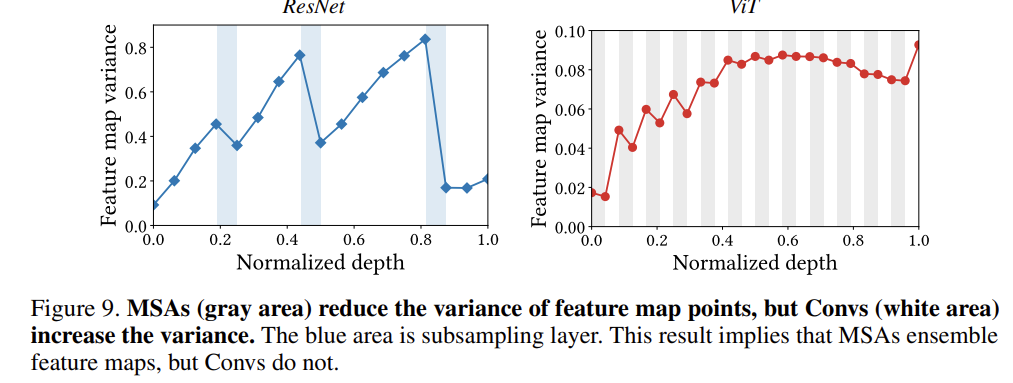
ViT의 경우 회색 영역에서 MSA가 feature map variance를 낮추고 있지만 ResNet의 경우 흰색 영역에서 Convolution이 feature map의 variance를 높이고 있습니다. MSA와 Convolution은 정말 다른 양상을 보여주는 연산인 것 같습니다.
그리고 저자는 여기서 두 가지의 패턴을 발견합니다.
- 신경망을 거칠 수록 variance가 더욱 누적되어 커지는 것을 확인할 수 있습니다.
- ResNet의 경우 feature map의 variance가 각 stage를 거칠 때마다 peak를 찍고 있습니다.
이러한 insight를 통해 저자는 "ResNet에서 각 stage 마다 마지막 부분에 MSA를 넣으면 feature map을 aggregate 하여 variance를 낮추고 학습을 더욱 도와 성능을 더 높일 수 있지 않을까?"라는 고민을 합니다.
How can we harmonize MSAs with Convs?
Convolution과 MSA는 서로 상호보완적으로 작동합니다. 따라서 저자는 두 방식의 장점만을 사용하는 새로운 모델을 제안하고자 합니다. 저자가 제안하는 방식으로 설계된 AlterNet은 기존의 CNN을 large data 뿐만 아니라 small data에서도 더 좋은 성능을 보여줍니다.
Designing Architecture
다시 아래의 그림을 보면 ResNet의 경우 feature map의 variance가 각 stage를 거칠 때마다 peak를 찍고 있습니다.
신경망의 stage 마다 유기적으로 연결된 모델이라면 feature map의 variance가 stage를 거칠 때마다 계속 증가하지는 않겠죠? 즉 이 말은 multi-stage 신경망은 individual model처럼 작동한다는 것입니다.
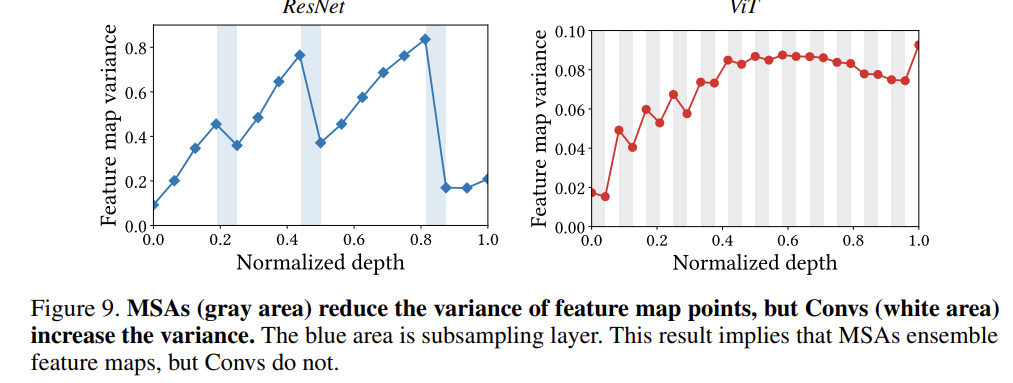
MSA는 계속 위에서 얘기했지만 smoothing 효과를 가지고 있기 때문에 feature map의 variance를 낮출 수 있습니다. 따라서 저자는 아래와 같은 Build-up rule을 제안합니다.

- Baseline CNN model의 마지막 stage의 Conv Block을 MSA Block이 뒤따라오는 Conv Block으로 대체합니다.
- 성능이 계속해서 개선될 때까지, 단순한 Conv Block을 MSA Block이 뒤따라오는 Conv Block으로 대체한다.
- 만약 성능이 개선되지 않았을 경우, 해당 스테이지에서는 위의 적용하지 않으며 다음 스테이지에서 다시 위의 규칙을 적용한다.
위의 규칙을 가지고 ResNet을 개선하면 아래와 같은 구조가 됩니다.
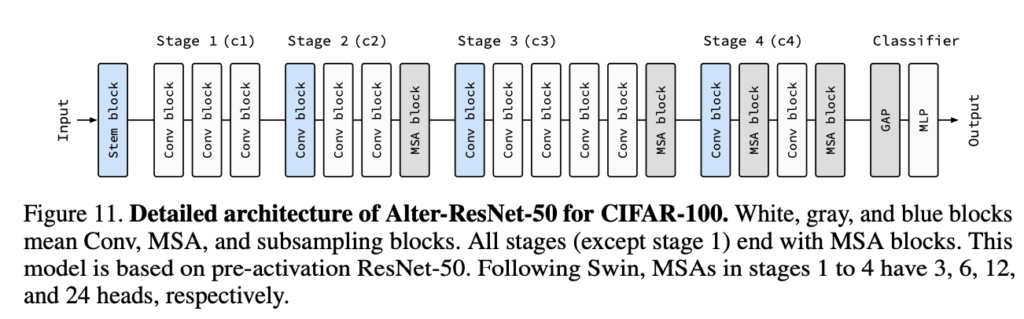
Performance
본문에서는 CIFAR-100에서의 실험 결과만을 가지고 있습니다. CIFAR-100은 small dataset입니다. 기존 vanilla ViT 같은 경우는 CNN에 비해 낮은 성능을 보여주었지만 저자가 제안하는 AlterNet은 ResNet 보다 더 높은 성능을 보여주며 Convolution과 MSA가 서로 조화를 이룰 수 있다고 주장합니다.
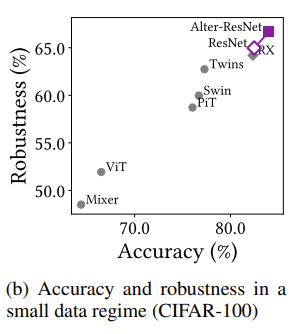
CIFAR-100만 보는 것은 조금 부족할 거 같아 appendix에 있는 ImageNet 비교 실험도 한번 확인해 보도록 하겠습니다.
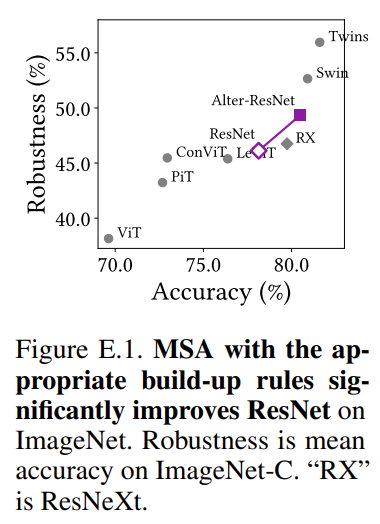
ImageNet에서도 좋은 양상을 보여주는 것 같습니다.
Conclusion
요즘 Vision Transformer 논문을 자주 읽는 것 같습니다. 이번 논문은 ViT와 Convolution의 차이를 좀 더 명확하게 알 수 있었던 논문인 것 같습니다.
제가 읽었던 몇 가지 Video Transformer 논문들은 long-range dependecy 덕분에 global informtation을 잘 capture 한다고 주장했습니다. 그런데 이번 논문을 읽고 나니 조금 머리가 아파지는 것 같습니다. 이번 논문만 놓고 보면 long-range dependency는 학습을 오히려 방해한다고 주장이 되어 있는데 다른 논문에서는 여전히 long-range dependency가 중요하게 여겨지기 때문입니다.
이번 논문이 image-level에서 그중에서도 classification을 target으로 분석이 이루어졌는데 더 다양한 task 그리고 더 다양한 data에 대해서도 깊이 있는 분석을 다루는 논문이 나왔으면 좋겠습니다.
리뷰 마치도록 하겠습니다.



