[arXiv 2016] An overview of gradient descent optimization algorithms

Before reivew

이번 주제는 gradient descent를 기반으로 하는 optimization algorithm들의 전체적인 concept을 살펴보고자 준비했습니다. 주제가 optimization이다 보니 어쩔 수 없이 Review에 수식이 많이 들어갔습니다. 최대한 이해하실 수 있도록 문장으로도 서술을 해놨으니 천천히 읽으시면 큰 무리는 없을 거라 생각이 듭니다. 저는 Adam 같은 경우는 그냥 막연하게 SGD 보다 좋더라 이렇게 알고 있어서 사용하고 있었는데 이번 기회에 optimization을 정리해보면서 어떤 점이 달라서 더 좋은 건지 이해하게 된 것 같습니다.

Introduction

Gradient descent 알고리즘은 Neural Network를 최적화시키는 방법으로 가장 흔하게 사용되는 방법입니다. 하지만 이런 알고리즘은 가끔 black-box optimizer로써 사용이 되기도 합니다. 명확한 이해와 설명 없이 그냥 경험적인 이유로 사용하는 경우가 종종 있습니다. 본 paper의 목표는 제목에서도 느낄 수 있듯이 다양한 gradient descent optimization 알고리즘들을 알아보고 어떻게 선택할지에 대한 이해를 가져다주는 것입니다.

 

Gradient descent 알고리즘은 $ objective function :  J(\theta ) $ 을 최소화하는 방법으로 사용이 되고 있습니다. 본격적으로 Gradient Descent를 설명하기 전에 간단한 미적분 얘기를 하고 넘어가겠습니다.

 

• Gradient and Multivariable Function

보통 Gradient Descent 알고리즘을 설명할 때 사용하는 가장 간단한 그림입니다. 현재 위치에서 기울기 방향으로 weight를 조금씩 움직여줘서 minimum에 도달하게 한다!! 이런 방식입니다. 이런 일변수 함수는 기울기의 방향이 왼쪽 오른쪽 두 가지뿐입니다. 하지만 사실 Objective Function 같은 경우는 저렇게 독립변수를 하나만 가지지 않습니다.

 

아래의 그림과 같이(사실 실제로는 시각화를 할 수 없는 landscpae를 가지겠죠) 여러 개의 각각 독립적인 weight를 가지는 Multivariable Function 다변수 함수로 구성이 됩니다. 다변수 함수 같은 경우는 어느 지점에서 기울기의 방향이 사방팔방으로 튈 수 있습니다. 이럴 때 바로 Gradient는 단순한 기울기가 아닌 어느 지점에서 최대 증가 방향으로의 기울기입니다.

 

우리는 Objective function의 최소 지점을 찾아야 하니 최대 증가 방향의 반대 방향으로 조금씩 움직여주겠다 라는 것이 Gradient Descent의 아이디어입니다.

$ weight=weight-\nabla_{\theta } Loss(\theta ) $ : weight update rule

Gradient Descent variants

본 Paper에서 소개하는 3가지 Gradient Descent 알고리즘이 있습니다. 핵심은 사용할 Data의 양과 Speed입니다.

 

• Batch Gradient Descent

Batch Gradient Descent는 하나의 Parameter를 Update 해줄 때 전체 train dataset을 이용하여 Update 해주는 방식입니다. 당연히 전체 train dataset을 이용하니 방향성은 정확하겠지만 수렴 속도가 굉장히 느리다는 단점이 있습니다. 본 Paper에서 Loss 함수가 Convex 하다면 반드시 Global Optimum에 도달할 수 있고 , Non-Convex 하다면 Local Optimum에는 반드시 도달할 수 있다고 나와있습니다.

 

• Stochastic Gradient Descent

Stochastic Gradient Descent는 하나의 Parameter를 Update 해줄 때 하나의 sample train data를 이용하여 Update 해주는 방식입니다. 당연히 데이터를 하나만 사용하니 전체적인 속도는 굉장히 빠르다는 장점이 있습니다. 다만 하나의 sample data만을 사용하기 때문에 방향이 전체적으로 변동성을 크게 가지게 됩니다. 이러한 변동성 때문에 Stochastic Gradient Descent 같은 경우는 local minima에 빠져도 꽤 잘 빠져나올 수 있다고 합니다. 하지만 변동성이 크기 때문에 정확한 값에 수렴을 할 수가 없을 수도 있습니다.

 

• Mini-Batch Gradient Descent

이제 이 Mini-Batch Gradient Descent는 Batch + Stochastic의 중간 버전이라고 생각하시면 됩니다. 적당한 그룹의 Batch-size를 설정하여 어느 정도 변동성을 줄이고 속도 또한 가져가는 Data양과 Speed 사이의 Trade-off 관계를 충족시킨 알고리즘이라고 보시면 됩니다.

Challenges

이런 Gradient Descent 알고리즘의 한계는 무엇이 있을 까요?

 

1. Learning rate의 설정 문제입니다.. learning rate가 너무 작으면, 수렴하는데 오랜 시간이 필요하고 반대로 너무 크면, 최솟값 근처에서 변동하거나 심지어 벗어날 수 있어 수렴을 방해합니다.
2. 동일한 learning rate가 모든 parameter 갱신에 적용됩니다. 만약 data가 sparse 하고 features가 제각각 다른 빈도수를 지니고 있으면, 이 모든 것들을 동일한 정도로 update 하면 안 됩니다. 드물게 발생하는 feature에 대해서는 크게 크게 update 해야 합니다.
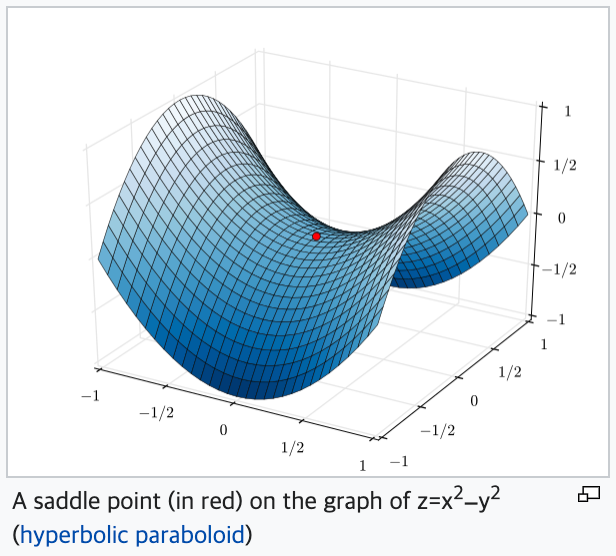
3. Global Optimum이 아닌 local minima와 안장점(saddle point) 빠질 위험이 있습니다. 안장점은 평면으로 둘러싸여 있어 기울기가 0인 지점을 의미합니다. 이런 안장점을 빠져나오는 데에도 Gradient Descent가 힘을 못쓴다고 합니다.

Gradient descent optimization algorithms

 

그림 출처 : https://github.com/heartcored98/Standalone-DeepLearning

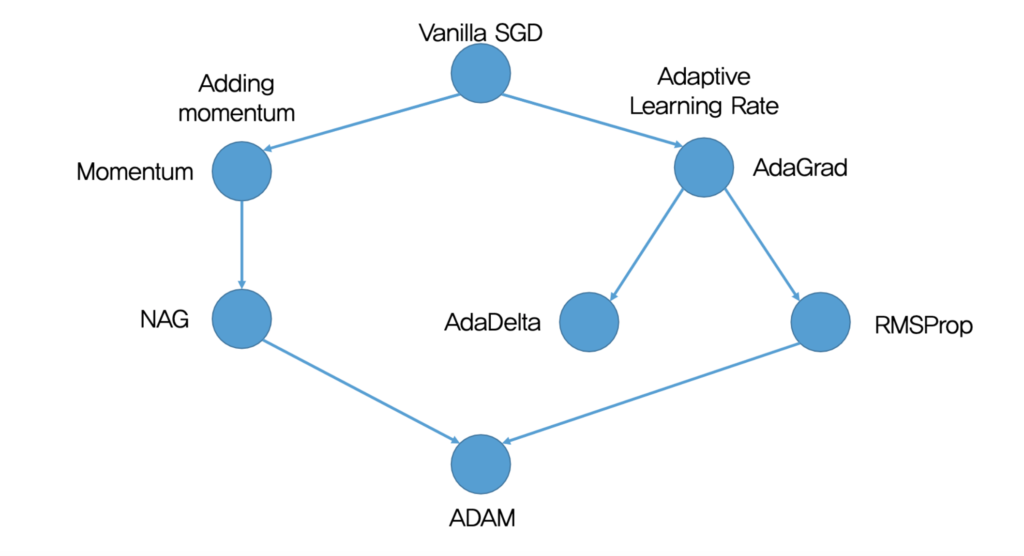
Vanilla SGD로부터 크게 두 가지의 흐름이 존재합니다.

 

첫 번째는 Momentum항을 추가하여 학습에 가속을 붙게 하고 local minima로부터 갇힐 위험을 줄여주는 방법 (Momentum , NAG)

 

두 번째는 Adaptive Learning rate로 모든 Parameter에 같은 learning rate를 적용하는 것이 아닌 , parameter의 update 빈도수에 따라 제각각 다른 Learning rate를 적용해주는 방법 (AdaGrad , RMSProp , AdaDelta)

 

정확히 무엇을 의미하는지 이제 한번 알아보도록 하겠습니다.

 

momentum

 

보통 관성을 이용한다고 표현합니다. 단순히 Gradient 방향으로만 움직이는 것이 아니라 이전 step 방향까지 고려해서 update 하는 방식입니다.

 

경사면에서 굴러가는 공의 방향과 속도를 바꾸는 게 어렵듯이 , SGD에 관성을 추가하여 갑자기 방향을 바꾸기 어렵게 하고 이전과 동일한 방향으로 나아갈 때는 가속이 작용되도록 합니다.

 

사실 관성이 붙는 다는 표현보다는 그냥 계산과정을 보시면 , Gradient가 벡터의 합으로 결정이 되는 구조인데 , 기존에 가던 방향과 새롭게 계산해준 Gradient 방향이 같다면 벡터 합으로 인해 더 큰 값이 gradient로 계산이 되는 것이고 이는 가속의 효과를 가져다줍니다.

 

반대로 기존에 가던 방향과 새롭게 계산해준 Gradient 방향이 다르더라도 , 벡터 합으로 인해 방향이 확 바뀌지 않게 됩니다.

 

방향을 바꾸기 어렵기 때문에 진동이 감소하고 , 동일한 방향에 대해서는 가속이 붙기 때문에 수렴 속도가 증가하게 됩니다.

또한 local minima에 빠져도 기존에 가던 관성이 존재하기 때문에 local minima를 뛰쳐나올 가능성도 증가하게 됩니다.

 

• $ v_{t}=\gamma v_{t}+\eta \nabla_{\theta } J(\theta ) $
• $ \theta =\theta -v_{t} $

하지만 단점도 존재합니다. 경사가 급한 내리막길에서는 관성이 크게 작용하여 가속이 심하게 붙을 것입니다. 경사를 타고 내려와 이제 global minima에 안착을 하고 싶은데 속도가 너무 빨라서 다시 그 minima를 벗어나 다른 곳으로 뛰쳐나갈 위험이 존재합니다. 즉 , 브레이크를 걸어야 하는 상황입니다. 이런 문제점을 보완한 것이 NAG , Nesterov acclerated gradient입니다.

 

Nesterov accelerated gradient

 

방식은 Momentum과 비슷한데 Gradient를 계산하는 방식이 조금 다릅니다.

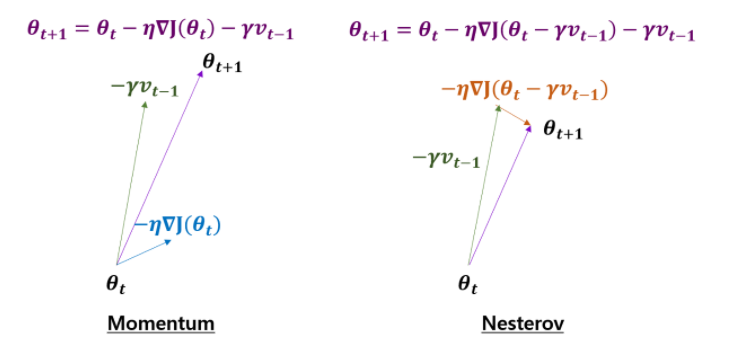
Momentum 방식에서는 momentum 방향과 Gradient 방향을 각각 구한 뒤 합쳐주는 방식이지만 Nesterov 방식에서는 일단 Momentum 방향으로 먼저 움직여주고 그 자리에서 Gradient 방향으로 update 하는 방식을 취하고 있습니다.

 

이렇게 하면 어떤 점이 좋냐 먼저 Momentum 같은 경우에는 멈춰야 하는 시점임에도 불구하고 관성으로 인해 멀리 벗어날 수 있다는 단점이 존재합니다. 하지만 NAG 같은 경우는 momentum 방향으로 움직이고 그 자리에서 어느 방향으로 이동할지를 결정하는 구조이기 때문에 보다 더 신중하다고 볼 수 있습니다.

 

• $ v_{t}=\gamma v_{t-1}+\eta \nabla_{\theta } J(\theta -\gamma v_{t-1}) $
• $ \theta =\theta -v_{t} $

내리막 길에서 momentum과 Gradient에 힘입어 그대로 쭉 내려가는 것이 아니라 momentum 만큼만 먼저 내려가 보고 그 위치가 minima 근처라면 이제 Gradient는 작을 테니깐 그제야 제자리를 찾아가 주는 좀 더 현명한 알고리즘이라고 보시면 되겠습니다.

 

Adagrad

 

이제는 살짝 방향이 달라집니다. 이전까지는 momentum을 기반으로 한 알고리즘이었다면 이제 핵심은 adaptive learning rate입니다.

 

한 줄로 요약하면 빈번하게 등장하는 parameter는 적게 갱신하고 , 드물게 등장하는 parameter는 크게 크게 갱신을 해주는 방법입니다. 갱신을 자주 해준 parameter들의 경우는 optimum에 가까이 있을 확률이 높기 때문에 작은 크기로 이동하면서 세밀한 값을 조정하고, 적게 변화한 변수들은 optimum 값에 도달하기 위해서는 많이 이동해야 할 확률이 높기 때문에 먼저 빠르게 loss 값을 줄이는 방향으로 이동하려는 방식이라고 생각할 수 있습니다.

 

• $ G_{t}=G_{t-1}+(\nabla_{\theta_{t} } J(\theta_{t, i} ))^{2} $
• $ \theta_{t+1} =\theta_{t} -\frac {\eta }{\sqrt {G_{t}+\epsilon } } \odot \nabla_{\theta_{t} } J(\theta_{t} ) $

 

$ G_{t} $라는 변수가 등장하는 데 설명을 드리면 본 Paper 상에서는 n by n 행렬의 대각 행렬이라고 표현을 해주는 데 n by n 행렬의 대각 성분은 결국 n 개의 성분이 존재하는 vector가 됩니다.

 

따라서 $ G_{t} $를 n개의 element를 가지는 vector로 정의해주겠습니다. 여기서 n은 parameter의 개수입니다.

$ G_{t} $가 점화식 형태로 정의가 되어있는데 쉽게 표현해주면 어느 시점 t까지 각각 parameter들의 Gradient 제곱을 누적 합 해준 것이라고 보시면 됩니다. 제곱을 더해주는 이유는 음수가 나와서 값이 줄어들면 정확한 비교가 힘들기 때문에 제곱을 해준 것입니다.

 

즉 , 학습을 시작했을 때부터 현재 학습이 진행되고 있는 시점 t까지 각각 parameter들이 얼마큼 갱신됐는지를 알려주는 값이라고 생각하시면 됩니다.

 

• $ \theta =<w_{1}, w_{2},\cdots w_{n-1}, w_{n}>$

• $ G=<\sum^{t}_{k=0} (\frac {\partial J(\theta )}{\partial w_{1, k}} )^{2},\sum^{t}_{k=0} (\frac {\partial J(\theta )}{\partial w_{2, k}} )^{2},\cdots ,\sum^{t}_{k=0} (\frac {\partial J(\theta )}{\partial w_{n, k}} )^{2}> $

예를 들어 G1이 비교적 큰 값을 가지고 있다 라는 말은 $ \theta =<w_{1}, w_{2},\cdots w_{n-1}, w_{n}> $ 중에서 w1이 자주 갱신됐다는 얘기일 테고 G3가 비교적 작은 값을 가지고 있다 라는 말은 w3가 적게 갱신됐다는 얘기입니다.

 

이제 이 $ G_{t} $라는 값을 learning rate에 나눠 줌으로써 $ G_{t} $가 크면 자주 갱신된 값이므로 적은 learning rate를 가지도록 $ G_{t} $가 작으면 적게 갱신된 값이므로 큰 learning rate를 가지도록 조정해주는 것입니다.

 

장점으로는 learning_rate를 이제 신경 써주지 않아도 된다고 합니다. 자동으로 맞춰주기 때문에 0.01 정도로만 초기화시켜두고 신경 써주지 않습니다. 다만 $ G_{t} $에는 계속 제곱 항이 더해지기 때문에 학습이 오래 진행되다 보면 step size가 너무 작아져 거의 움직이지 않는다는 단점이 존재합니다. 이를 보완하여 고친 알고리즘이 Adadelta와 RMSProp입니다.

 

RMSProp

 

Adagrad의 문제는 학습 시간이 길어지면 $ G_{t} $ 에 계속 Gradient의 제곱 항이 더해지므로 $ G_{t} $ 값이 계속 커지게 되고 결국 Learning rate가 매우 작아져 step이 멈춰 버립니다.

 

지금 말씀드릴 RMSProp는 논문으로 나온 방법은 아니고 제프리 힌턴 교수님이 코세라 강의 중에 고안하신 방법입니다.

$ G_{t} $를 구해줄 때 막연하게 제곱을 쭉쭉 더해주는 것이 아니라 일종의 가중치를 곱해줘서 $ G_{t} $가 적정크기로 존재할 수 있도록 제한 해준 알고리즘입니다.

 

• $ \theta_{t+1} =\theta_{t} -\frac {\eta }{\sqrt {G_{t}+\epsilon } } \odot \nabla_{\theta_{t} } J(\theta_{t} ) $
• $ G_{t}=\gamma G_{t-1}+(1-\gamma )(\nabla_{\theta } J(\theta ))^{2} $

$ \gamma $라는 decaying factor라는 weight들을 곱해줌으로 써 train을 오래 하여도 $ G_{t} $가 계속해서 커지지 않습니다. 따라서 learning rate가 0으로 작아져버리는 문제는 어느 정도 해소가 됩니다.

 

Adadelta

 

Adadelta는 지난주에 다루었던 Adagrad의 확장판입니다. Adagrad의 문제점이 어떤 문제였는지 빠르게 짚어보고 가겠습니다. Adagrad에서 parameter들이 얼마나 자주 update 되었는지 기록하기 위해 $ G_{t} $라는 vector를 정의해주었습니다. 다만 이 $ G_{t} $ 구해주는 과정에서 $ G_{t}=G_{t-1}+(\nabla_{\theta_{t} } J(\theta_{t} ))^{2} $ Gradient의 제곱항이 계속 더해지므로 $ \frac {\eta }{\sqrt {G_{t}+\epsilon } } $ 값이 계속 작아지면서 step이 멈춰버리는 단점이 존재했습니다. RMSProp는 이런 단점을 $ G_{t} $ 구해주는 과정에서 decaying factor $ \gamma $ 값을 곱해줘서 조절해주고 있었습니다.

 

• $ G_{t+1}=\gamma G_{t}+(1-\gamma )(\nabla_{\theta } J(\theta ))^{2} $

• $ s_{t+1}=\gamma s_{t}+(1-\gamma )\triangle \theta^{2} $

• $ \triangle \theta =\frac{\sqrt{s_{t}+\epsilon } }{\sqrt {G_{t}+\epsilon } } \odot \nabla_{\theta } J(\theta_{t} ) $

• $ \theta_{t+1} =\theta_{t} -\triangle \theta $

Adadelta의 전체적인 방향은 RMSProp와 비슷합니다. $ G_{t} $를 구해주는 과정이 동일하지만 parameter를 update 해줄 때 이제 learning rate $ \eta $를 사용하지 않습니다. $ s_{t} $라는 vector를 이용하여 learning rate를 대체하고 있는데 $ G_{t} $는 parameter가 얼마나 자주 갱신됐는지를 담고 있는 vector라면 $ s_{t} $는 parameter가 얼마큼 갱신이 됐는지 parameter의 누적 변화량을 담고 있다고 보시면 됩니다.

 

한 가지 의문이 들어야 하는 부분은 그냥 RMSProp처럼 $ \frac {\eta }{\sqrt {G_{t}+\epsilon } } $ 이렇게 learning 쓰면 되지 뭐하러 $ s_{t} $ 계산을 해서 메모리와 computation을 낭비하나 이런 의문이 들지만 저자가 이제 얘기하길 어떤 단위를 맞춰주기 위한 작업이라고 합니다.

 

$ \theta_{t+1} =\theta_{t} -\triangle \theta $ 이 부분을 다시 살펴보면 $ \nabla \theta $의 단위가 $ \theta_{t} $ 랑 같게 맞춰야 하지 않겠느냐 이런 관점에 Adadelta를 살펴보면 $ \nabla_{\theta_{t} } J(\theta_{t} ) $ 이 녀석의 단위는 우선 $ \theta_{t} $ 와 같을 수가 없습니다. 미분을 했기 때문입니다. $ \frac {1}{\sqrt {G_{t}+\epsilon } } $ 의 단위는 Loss 함수의 2차 Gradient의 제곱근이기 때문에 $ \nabla_{\theta_{t} } J(\theta_{t} ) $ 이 친구와 단위가 같게 됩니다. 둘은 분자 분모에 위치하고 있기 때문에 상쇄가 됐고 이제 $ \sqrt {s_{t}+\epsilon } $ 이 친구의 단위만 따져 보면 되는데 $ s_{t+1}=\gamma s_{t}+(1-\gamma )\triangle \theta^{2} $ 보시다시피 단순히 $ \theta_{t} $ 변화량의 제곱의 루트가 씌워진 형태이므로 단위는 $ \theta_{t} $ == $ \sqrt {s_{t}+\epsilon } $ 이렇게 되고 결국 update 과정에서 단위가 통일되게 됩니다.

 

찾아보면서 확인해봤을 때 실제로는 Adadelta가 Adagrad에 비해 무조건 좋은 것은 아닌가 봅니다. Adagrad가 더 잘 될 때도 있고 Adadelta가 더 잘 될 때도 있다고 합니다.

 

Adam

 

이제 바로 그 유명한 Adam입니다. 쉽게 설명하면 두 가지로 나눠진 흐름을 다시 한데 묶어놓은 방법론입니다. Momentum으로 얻을 수 있는 이점과 Adaptive learning rate를 이용해서 얻을 수 있는 이점을 동시에 챙긴 균형 잡힌 Optimizer라고 생각하시면 됩니다.

 

• $ m_{t}=\beta_{1} m_{t-1}+(1-\beta_{1} )\nabla_{\theta } J(\theta ) $

• $ v_{t}=\beta_{1} v_{t-1}+(1-\beta_{1} )(\nabla_{\theta } J(\theta ))^{2} $

• $ \hat{m}_{t} =\frac {m_{t}}{1-\beta^{t}_{1} } $ , $ \hat {v}_{t} =\frac {v_{t}}{1-\beta^{t}_{2} } $ --- (1)

• $ \theta_{t+1} =\theta_{t} -\frac{\eta }{\sqrt {\hat {v}_{t} } +\epsilon } \hat {m}_{t} $

paramter를 update 해주는 과정은 전과 비슷합니다. Gradient 부분에 $ \hat{m}_{t} $이 들어가 있는 것을 제외하고는 이전과 동일합니다. 다만 $ \beta_{1} =0.9,\beta_{2} =0.999,\epsilon =10^{-8} $ 이렇게 값을 취해주면 학습 초기에 parameter update가 너무 크게 크게 발생합니다. 대입해보면 금방 확인할 수 있습니다. 그렇기 때문에 (1)에서 값을 보정해주는 것입니다. 이는 학습 초기에만 너무 step이 튀지 않게끔 조절해주는 역학을 하면 학습이 나중에 진행되면 크게 상관이 없다고 합니다. 핵심은 momentum의 개념과 Adaptive learning rate의 개념을 동시에 사용했다는 점입니다.

 

Visualization of algorithms

 

 

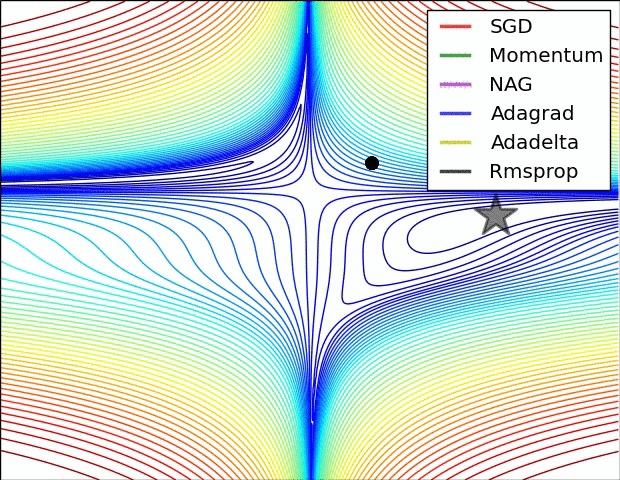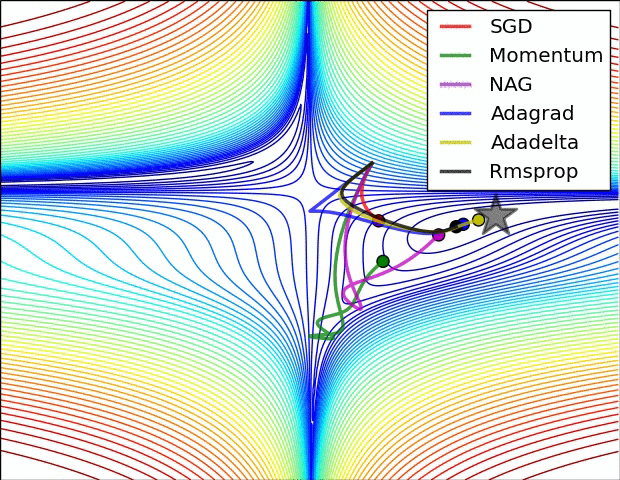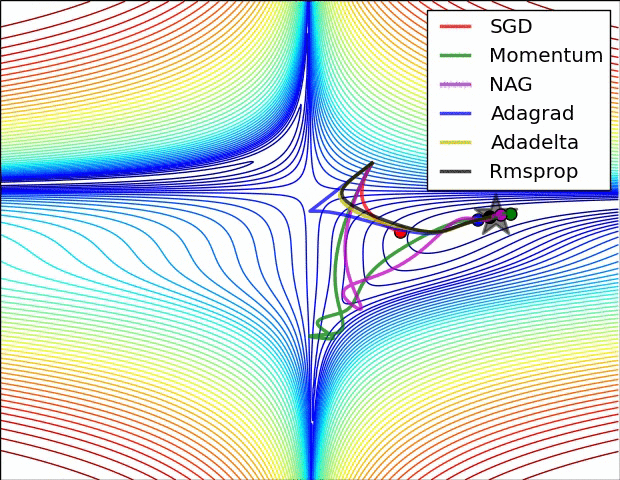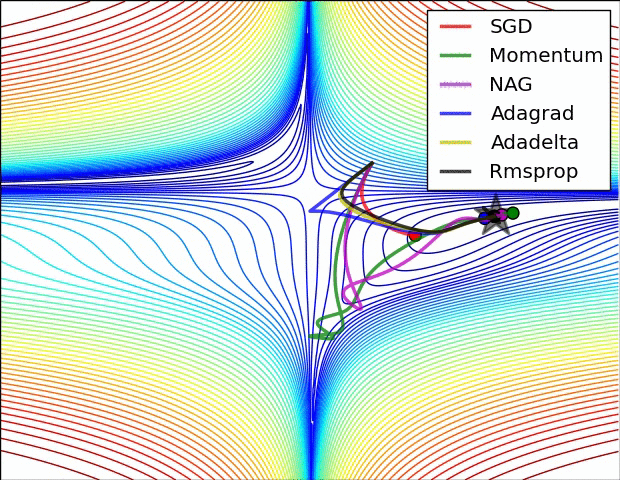
Gradient Descent algorithm들의 큰 흐름을 살펴보았고 이제 본 Paper에 실려있던 그림을 확인해보겠습니다. 위의 그림을 살펴보면 optimizer 별로 loss surface상에서 경로들을 비교하면서 확인할 수 있습니다. 모두 같은 point에서 시작했지만 다른 경로로 minima에 수렴하고 있습니다. Adagrad , Adadelta , Rmsprop 같은 경우는 즉시 수렴하는 것을 확인할 수 있고 , momentum과 NAG는 조금 방향을 헤매는 것을 확인할 수 있습니다. momentum과 NAG사이에서도 NAG가 좀 더 빠르게 수렴하는 것을 확인할 수 있는데 Review1에서 확인했던 이유이지 않나 싶습니다.

 

 

SGD를 제외하고서는 모두 saddle point에서 탈출하는 것을 확인할 수 있습니다.

Additional strategies for optimizing SGD

 

• Shuffling and Curriculum Learning

일반적으로 model을 학습을 시킬 때 어떤 data에 대한 편향을 가지지 않도록 하기 위해서 training dataset을 제공하는 것이 중요했습니다. 따라서 우리가 data를 건네줄 때 일반적으로 shuffle을 시켜서 주는 것이 당연했습니다. 이러한 방법이 SGD에 도움이 된다고 합니다.

 

또한 이렇게 데이터를 무작위로 섞어서 주지 않는 방법도 있다고 합니다. Curriculum learning이라는 것인데  일반적으로 사람이 초급 수준의 학습부터 대학 수준의 학습내용까지 긴 기간을 가지고 학습하는 경우처럼, 이를 머신러닝의 학습에 적용하는 것입니다. 즉 , 커리큘럼 학습은 처음에는 모델한테 쉬운 샘플만 보여주다가 점차 어려운 샘플을 보여주는 것입니다. 학습 시에 전체 데이터를 한 번에 학습시키는 것보다 처음에는 쉬운 데이터 그다음으로 어려운 데이터 순으로 제공하는 것을 의미합니다.

 

• Batch Normalization

학습을 용이하게 하기 위해 종종 data들의 정규화를 진행해주곤 합니다. 이러한 정규화된 분포의 특성을 layer들을 통과하면서 잃어버리게 되고 학습의 저하를 일으키게 합니다. 이때 Batch Norm을 적용해줌으로써 각 Layer에 들어가는 input data들이 동일한 분포를 가질 수 있도록 해줍니다. 결과적으로 수렴 속도가 빨라지고 , 모델의 성능에도 좋은 효과를 볼 수 있다고 합니다.

 

• Early stopping

모델이 너무 많은 Epoch를 돌다 보면 training dataset에 overfitting 되어버리기 때문에 validation error를 측정하다가 개선의 여지가 보이지 않으면 학습을 중단하는 것을 의미합니다.

 

• Gradient noise

다음과 같이 gradient에 Gaussian noise를 첨가해주는 것을 의미합니다.

 

$ g_{t, i}=g_{t, i}+N(0,\sigma^{2}_{t} ) $ , $ \sigma^{2}_{t} =\frac {\eta }{(1+t)^{\gamma }} $

 

자세히 이유는 다루고 있지 않는데 , 이렇게 noise를 첨가해주면 network가 좀 더 initialization에 robust 해진다고 합니다. 모델이 local minima를 탈출할 기회를 더 많이 가진다고 해서 그렇다고 합니다. 개인적인 생각으론 noise가 minima에 빠져있는 상황에 일종의 action을 주는 event 같은 느낌인 것 같습니다.

Conclusion

2번에 걸쳐서 gradient descent optimization algorithm에 대해서 알아봤습니다. 처음에 가장 기본적인 gradient descent의 세 가지 방법론을 알아봤고(batch , stochastic , mini-batch) gradient descent가 가지는 한계점에 대해서 살펴봤습니다.

 

그 한계점에 기반해서 Gradient Descent를 보완시킨 여러 가지의 optimizer들을 수식을 통해 작동원리를 파악했고 이러한 optimizer 전략 외의 다른 방법들 또한 간단하게 알아볼 수 있었습니다.

 

Review를 진행하면서 Gradient Descent Optimization 부분에 관해서 과거 연구자들의 고민의 발자취 들을 살펴볼 수 있었던 Paper였습니다. Review 읽어주셔서 감사합니다.