Before Review
이번에도 Weakly supervised temporal localization 논문으로 준비를 했습니다. LSTM을 공부할 때 접했던 개념인 memory 개념을 Weakly supervised temporal action localization에 처음으로 도입한 논문이라고 합니다.
Weakly supervised temporal localization 관련 리뷰는 이전에도 몇 개 진행을 했었는데 아래에 링크를 첨부하도록 하겠습니다. 본 리뷰부터 진행되는 Weakly supervised temporal localization 리뷰에서는 task에 대한 자세한 설명은 다루지 않을 것이기 때문에 잘 모르시는 분들은 과거의 리뷰를 통해 이해해주시면 감사하겠습니다.
[1] [CVPR 2021] Weakly Supervised Action Selection Learning in Video
[CVPR 2021] Weakly Supervised Action Selection Learning in Video
Before Review 이번에 진행할 리뷰 역시 Temporal Localization 논문으로 가져왔습니다. 이전까지는 Supervised 방식 위주로 논문을 읽었는 데, 이번에는 Weakly Supervised 기반의 방법론 논문을 읽어보았습니다..
taek-guen.tistory.com
[2] [2020 AAAI] Background Suppression Network for Temporal Action Localization
[2020 AAAI] Background Suppression Network for Temporal Action Localization
Before Review 이번에도 Weakly Supervised Temporal Localization 논문을 들고 왔습니다. 2020년도 AAAI에 나온 논문이고 반가운 건 한국인이 저자인 논문이네요. 네이버 클로바와 연세대학교 연구진이 같이 작성
taek-guen.tistory.com
[4] [TPAMI 2021] Background-Click Supervision for Temporal Action Localization
[TPAMI 2021] Background-Click Supervision for Temporal Action Localization
Before Review 이번 논문 리뷰는 Temporal Action Localization으로 준비했습니다. 그중 Supervised 방식이 아니라, Weakly Supervised 방식으로 논문을 선택했습니다. TPAMI 저널에 투고된 논문은 처음 읽어보는..
taek-guen.tistory.com
리뷰 시작하도록 하겠습니다.
Introduction
Weakly Supervised temporal localization은 비디오 레벨의 라벨만을 사용하기 때문에 annotation cost를 완화시킬 수 있다는 장점이 있지만, 난도가 높은 task로 근본적으로 두 가지의 문제점을 가지게 됩니다.
frame 단위의 supervision이 없기 때문에 근본적으로 localization을 불완전하게 수행하게 되며 이를 localization completeness problem이라고 저자는 얘기합니다. 또한 비디오에는 상당한 양의 background frame이 존재하게 되는데, 마찬가지로 frame 단위의 supervision이 없기 때문에 action frame과 background frame을 구별하는 데 어려움을 겪게 됩니다.
본 논문에서는 이러한 문제를 background inference라고 정의를 하고 있네요.
이러한 문제를 해결하기 위해서 이전까지의 방법론들은 여러 가지 시도를 해왔습니다. 특정 구간을 지웠다가 맞추는 1) erasing strategy, 다양한 branch를 통해 비디오의 다양한 부분을 이해하는 2) multi-branch architecture, attention 기반으로 action과 background를 구분할 수 있게 feature를 만드는 3) attention based approach 등이 있습니다.
이렇게 저자는 이전의 연구들을 모두 종합해본 결과 세 가지의 중요한 observation을 얻을 수 있었다고 합니다.
- Sharing Unit : 서로 다른 action이라도 공통적인 action을 특성을 공유할 수 있다.
- Sparsity : Untrimmed video에서 action을 포함하는 부분은 굉장히 적다. 즉, background가 대부분이라는 소리
- Smootheness : 정확한 Localization을 위해서는 CAS(Class Activation Sequence)가 smooth 하게 나와야 한다.
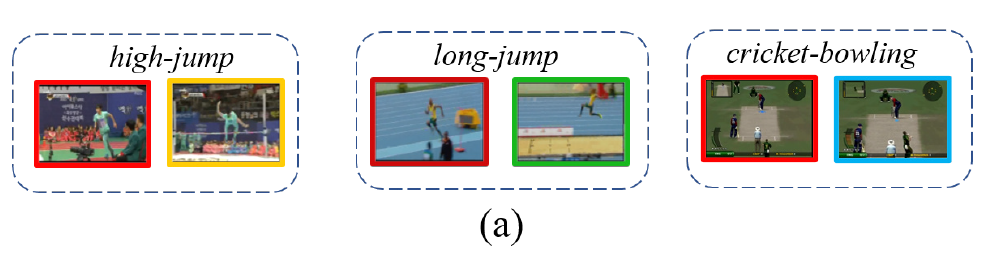
자 여기 high-jump, long-jump, cricket-bowling이라는 서로 다른 action이 있습니다. 하지만 세 가지의 action 모두 달리고 있다는 공통적인 성질을 가지고 있습니다. 그래서 action의 category는 달라도 그들끼리 공통적으로 공유하고 있는 action unit이 있다라고 저자는 얘기하고 있는 것입니다.
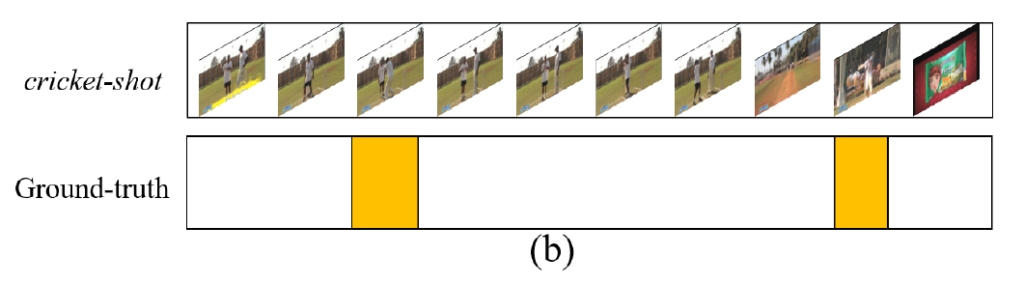
또한 Untrimmed Video에서는 action이 굉장히 드물게 등장합니다. temporal action localization에서 정의하는 action은 정말 그 action 자체를 의미하며, action을 준비하는 과정이나 action을 마친 후 마무리하는 장면은 background에 해당됩니다.
그래서 정말 실제 action 자체를 하고 있는 부분은 많지 않습니다. 이렇기 때문에 저자는 Sparsity라는 특징을 가지고 있다고 얘기하고 있습니다.
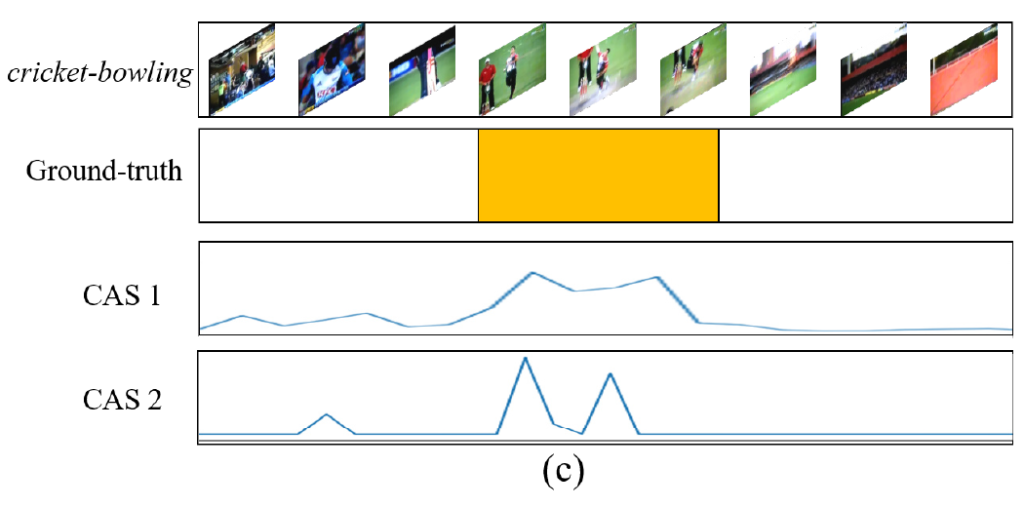
마지막으로 Smootheness입니다. Weakly supervised temporal localization에서는 Class Activation Sequence라는 것을 추출하여 Localization을 수행합니다. CAS가 무엇인지 모르겠다면 이전 리뷰들을 참고해주시길 바랍니다. CAS가 크게 반응했을 때를 action이라고 간주하기 때문에 action 구간 근처에는 CAS가 크게 활성화가 됩니다.
CAS1와 CAS2의 차이는 CAS1이 좀 더 action 구간에서 높고 부드럽게 존재한다는 것입니다. action 구간은 웬만해서 연속적으로 나타납니다. 물론 짧게 짧게 등장하는 동영상들이 몇 개 있지만 그런 영상들은 어려운 영상이기 때문에 논외라 두고 평균적으로는 action 구간 자체는 continous 하게 존재하게 됩니다.
CAS2처럼 activation이 연속적이지 않고 끊어서 나오게 되면 평균적인 Localization 성능이 떨어지게 됩니다.
이 세 가지의 특성이 성공적인 temporal localization을 수행하는 데 있어서 중요하지만 한 번도 다뤄지지 않았다고 저자는 얘기합니다. 그러나 video level의 라벨만을 가지고 이 세 가지의 특성을 한 번에 modeling 하는 것은 꽤나 어려운 작업이겠죠.
그래서 저자의 contribution은 당연히 이러한 세 가지의 특성을 end-to-end 방식으로 한꺼번에 modeling 할 수 있는 구조를 제안했다는 점에 있습니다. 그럼 이제부터 그 제안된 방법론에 대해서 알아보도록 하겠습니다.
Proposed Method
Notations and Preliminaries
- Input Video : $\{ v_{i}\}^{N}_{i=1} $
- Annotation : $y_{i}\in R^{C}$
- Model prediction : ${(c,s,e,q)}$
최종적으로 예측하는 값은 proposal 집합을 예측하게 되며 각 proposal은 (action category, start time, end time, confidence scroe)로 구성이 되어 있습니다. 전형적인 weakly supervised temporal localization과 문제 정의는 동일합니다.
Backbone으로 뽑은 Feature $X_{i}$가 있을 때, 사실 이 backbone feature는 action recognition dataset으로 사전학습이 된 feature이기 때문에 localization에 바로 사용하기에는 적합하지 않을 수 있습니다. 따라서 저자는 task-adaption layer라는 것을 붙여서 새로운 feature로 먼저 embedding을 시키게 됩니다.
- $X^{e}_{i}=ReLU(W^{emb}\ast X_{i}+b^{emb})\in R^{l_{i}\times F}$
여기서 $l_{i}$는 비디오 내부에 존재하는 segment의 개수이고 segment는 중복되지 않는 16개의 frame을 하나의 segment라 정의합니다. 즉, 비디오가 160 프레임으로 구성되어있다면 이 비디오에는 10개의 Segment가 있다는 셈이죠.
이제 아래부터는 전반적인 모델 구조에 대해서 알아보도록 하겠습니다. 전반적인 모델은 크게 세 가지로 분류할 수 있습니다. 1) feature extraction, 2) memory bank construction, 3) memory bank for classification and updating
feature extraction은 방금 알아보았으니 나머지 memory bank와 관련된 부분에 대해서 알아보도록 하겠습니다.
Memory Bank Construction
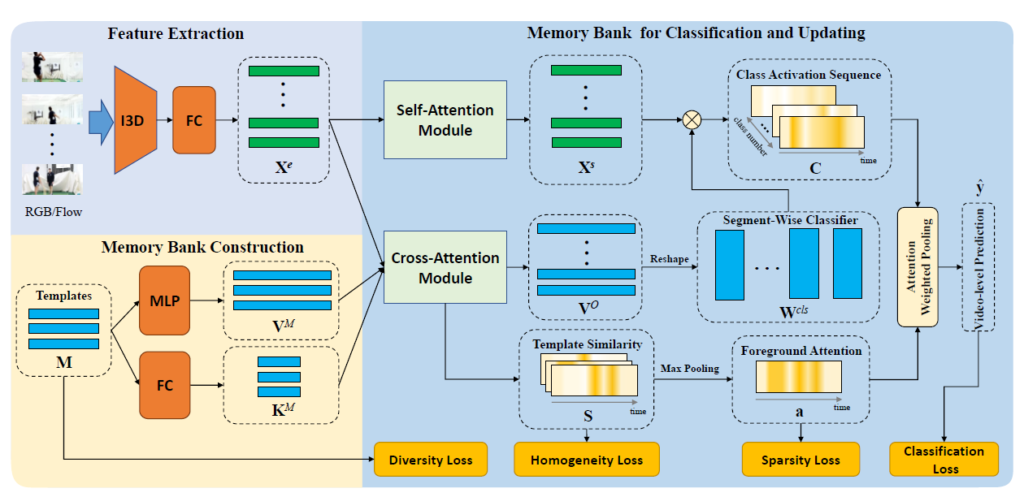
앞서 언급한 3가지의 특성을 jointly 하게 modeling 하기 위해서 저자는 memory bank라는 것을 도입하였습니다. 이 memory bank에는 action unit template이 들어가 있어 action 전반적으로 발현될 수 있는 공통의 action unit을 만들어놓는다 생각하면 됩니다.
아래의 그림을 보면 Memory Bank Construction 부분을 볼 수 있습니다. 초기에 Templates를 랜덤 하게 생성한 뒤 MLP layer와 FC Layer를 사용해 key, value를 생성하게 됩니다.
key역할은 video segment와의 similarity를 계산하기 위한 목적이고 value의 역할은 segment-wise의 classification을 위한 classifier를 만드는 데 사용이 됩니다. Segment마다 동일한 weight를 가지고 classification을 하는 것이 아니라 segment의 motion이나 appearance에 맞추어 adaptive 하게 classification을 한다고 생각하면 됩니다.
- $M\in R^{K\times F}$ : K개의 template를 가지고 있고 template의 차원은 Feature의 차원 $F$와 동일합니다.
- $K^{M}=Enc_{K}(M)\in R^{K\times (F/m)}$ : key를 생성해주고 있고, 연산의 효율성을 위해 m이라는 hyperparameter로 차원을 축소해주고 있습니다.
- $V^{M}=Enc_{V}(M)\in R^{K\times CF}$ : value를 생성해주고 있고, 여기서는 차원을 $CF$로 투영을 시켜주고 있습니다.
다시 한번 정리해보면 key는 template의 정보를 담고 있다고 보면 되고 그 정보들은 appearance나 motion 정보라 보면 됩니다. 이를 통해 특정 video segment와 template matching을 통해 similarity를 계산하는 역할을 담당하며 value는 각 templates에 해당하는 classifier를 저장하고 이를 가지고 segment wise의 classification을 수행하게 됩니다.
Memory Bank for Classification
그렇다면 이 memory bank를 이용한 video level classification은 어떻게 진행이 되는지 알아보도록 하겠습니다. 먼저 embedding feature를 바로 사용하는 것이 아니라 query로 만들어줍니다. 물리적인 의미를 담고 있지는 않기에 그냥 단순히 새로운 공간으로 projection 시켜주면서 memory bank의 key와 차원을 맞춰주기 위해 진행했다고 이해했습니다.
- $Q_{i}\in R^{l_{i}\times F/m}$
그러고 나서 embedding feature와 그에 해당하는 query가 두 가지의 attention module을 거치게 됩니다.
그림에서도 볼 수 있듯, Self-Attention Module과 Cross-Attention Module을 거치는 과정을 확인할 수 있습니다. 먼저 Self-Attention module은 query를 이용하여 video segment끼리의 similarity를 계산하게 됩니다.
이를 적용한 새로운 feature를 만들게 되는 것이죠. segment끼리의 의존성을 학습한다고 보면 되고 이를 통해 global 한 context 정보를 투입할 수 있게 만들어줍니다.
- $X^{s}_{i}=(softmax(\frac{Q_{i}Q^{T}_{i}}{\sqrt{F/m} } )+I)X^{e}_{i}$
identity matrix를 사용하여 original 정보를 보존함과 동시에 similarity기반의 attention이 적용된 새로운 정보를 추가했다고 보면 됩니다.
다음으로 Cross-Attention Module에서는 Segment-wise Classifier를 얻기 위해 설계되었습니다. 이제는 비디오끼리가 아니라 비디오와 template 간의 유사도를 계산하게 됩니다. 이 유사도를 바탕으로 이제는 segment 단위의 classifier를 얻을 수 있는데 이때 사용되는 것이 memory bank의 value입니다.
- $S_{i}=sigmoid(\frac{Q_{i}\left( K^{M}\right)^{T} }{\sqrt{F/m} } )\in R^{l^{}_{i}\times K}$
memory bank의 key와 embedding feature의 query를 가지고 template과 segment 간의 similarity를 계산해주고 있습니다. 그리고 이러한 similarity를 가지고 segment-wise classifier를 memory bank의 value를 활용하여 생성해주게 됩니다.
- $V^{O}_{i}=S_{i}V^{M}\in R^{l_{i}\times CF}$
결국 segment마다 다른 weight를 가지고 CAS(class activation sequence)를 만들어내겠다는 소리입니다. 아까 새롭게 Self attention을 적용한 video feature $X^{s}\in R^{l_{i}\times F}$가 있고 segment마다 다른 weight를 가지는 segment-wise classifier $W^{cls}\in R^{l_{i}\times F\times C}$가 있습니다.
여기서 아까 template와 segment 간 similarity를 구했던 $S_{i}$에 template 차원에 대해서 max-pooling을 취해서 foreground attention weight $a_{i}\in R^{l_{i}}$를 구해줍니다.
무슨 소리냐면 모든 templater 간의 similairty 중 최댓값을 본다는 것은 action의 상관없이 그 segment 자체의 action score를 나타낼 수 있게 됩니다. 어떤 segment가 모든 template과의 similarity가 낮다는 것은 background segment일 확률이 높다는 의미겠죠.
- $a_{i}=MaxPool(S_{i})\in R^{l_{i}}$
그러고 나서 이제야 video-level classification을 할 수 있습니다.
- $\hat{y}_{i} =softmax\left( \frac{1}{l_{i}} \sum^{l_{i}}_{i=1} a_{i}(t)\left( X^{s}_{i}(t)W^{cls}_{i}(t)\right) \right) $
foreground attention과 segment-wise classifier를 가지고 segment level의 score vector를 구할 수 있고 이를 평균 내주어서 video level score를 만들어주고 있는 모습입니다.
video level score를 만들어주었다면 마무리는 cross-entropy loss를 가지고 학습을 시키면 끝이 나겠네요.
- $L_{cls}=-\frac{1}{B} \sum^{B}_{i=1} \sum^{C}_{j=1} y_{i}(j)log\left( \hat{y}_{i} \left( j\right) \right) $
Memory Bank Updating
memory bank를 update 하기 위해서는 classification loss만을 가지고는 충분하지 않습니다. 그렇다면 우선 memory bank가 가져야 할 특성에 대해서 알아보도록 하겠습니다.
- memory bank에 속한 template는 유일해야 합니다. 즉, template끼리는 비슷하지 말아야 하는 것이지요.
- memory bank에 속한 template는 유의미해야 합니다. 즉, 모든 template은 어떠한 action의 성질을 포착할 수 있는 유의미한 정보를 담고 있어야 합니다.
- memory bank에 속한 template는 비디오 내에 sparse 하게 존재하는 action segment와 큰 similiary를 가져야 합니다.
Diversity Loss
자 하나씩 얘기해보겠습니다. template 끼리 유일해야 한다는 의미는 무엇을 의미할까요? template 끼리 similarity를 계산했을 때 같은 template 끼리의 유사도는 1에 가까워야 하고 다른 template 끼리의 유사도는 0에 가까워야 template들이 unique 하다고 얘기할 수 있을 것 같습니다. 여기서 frobenius norm이 등장하는 데 벡터나 행렬의 크기를 일반화시킨 형태라고 보면 됩니다.
- $\parallel A\parallel_{F} =\sqrt{\sum^{m}_{i=1} \sum^{n}_{j=1} \mid a_{ij}\mid^{2} } $ : 행렬의 각 원소를 제곱 후 모두 더한 뒤 제곱근을 취한 형태입니다. 이게 frobenius norm의 정의입니다.
그러고 나서 Diversity Loss는 다음과 같이 정의됩니다.
- $L_{d}=\parallel MM^{T}-I\parallel_{F} $
사실 이거 해석하는 게 조금 어려웠는데 조금만 생각해보면 그렇게 또 어렵지는 않습니다. Frobenius norm의 값이 작아지려면 당연히 행렬의 각 원소들이 0에 가까운 값을 가지고 있으면 됩니다. $MM^{T}$의 대각 성분은 같은 template 끼리의 유사도이고 대각 성분이 아닌 성분들은 서로 다른 template 끼리의 유사도입니다.
이러한 상황에서 항등 행렬(I)을 빼주게 된다면 대각 성분에 1을 빼주는 형태입니다. 우리가 원하는 상황은 같은 template 끼리의 유사도는 1에 가까워야 하고 다른 template 끼리의 유사도는 0에 가까워야 하는 상황이라 위에서 정리했습니다.
즉, 그러한 방향으로 최적화가 되는 것이라면 $MM^{T}-I$의 모든 성분은 0에 가까워지며 frobenius norm으로 정의된 Diversity Loss term은 0으로 수렴을 하게 되겠죠.
Homogeneity Loss
위에서 정의한 Diversity Loss를 통해 각 template들이 unique 해질 수 있다는 성질은 어느 정도 보장할 수 있지만, 모든 template들이 의미가 있다는 것은 아닙니다. template이 의미가 없다는 얘기는 모든 video segment와의 유사도가 낮게 나온다는 의미로 action 에 대한 유의미한 정보를 내포하고 있지 않으므로 이러한 반응이 나온다는 얘기겠죠.
따라서 Video Segment와 template 간의 similarity가 모두 골고루 uniform 하게 발생하면 모든 template이 각자의 역할을 어느 정도 수행하고 있다 볼 수 있을 것 같습니다.
위에서 Video segment와 template 간의 similarity를 담고 있는 행렬 $S_{i}\in R^{l_{i}\times K}$를 정의했습니다. 여기서 시간축에 대해서 sum pooling과 softmax를 통해 1D vector $P_{i}=softmax\left( \sum^{l_{i}}_{i=1} S_{i}(t)\right) $를 만들어줍니다.
이 vector는 template들의 score vector로 score가 클수록 template이 다른 video segment들과 잘 반응을 했다는 의미로 보면 됩니다.
우리의 목적은 template마다 score가 들쭉날쭉한 것이 아니라 골고루 모두 제 역할을 가지도록 만드는 게 목적이기 때문에 L2-regularization을 하면 이러한 목적을 달성할 수 있습니다. L2-regularization이 parameter의 scale과 분포를 비슷하게 만들어주는 역할을 수행하기 때문이죠.
- $L_{h}=\parallel \frac{1}{B} \sum^{B}_{i=1} p^{O}_{i}\parallel_{2} $
이렇게 homogeneity Loss를 정의할 수 있습니다.
Sparsity Loss
위에서 우리가 $a_{i}=MaxPool(S_{i})\in R^{l_{i}}$를 가지고 foreground attention을 수행한다고 알아봤습니다. 여기서 정말로 진짜 action에만 attention을 줄 수 있게 $a_{i}$의 분포를 조금 수정해야 할 필요가 있습니다. 진짜 action인 구간에만 큰 값을 가지고 background에는 작은 값을 가질 수 있게 해야겠죠.
L1-regularization은 특정 값을 줄이고 특정 값을 키우는 정규화를 수행하여 parameter마다의 영향력을 늘이고 줄일 수 있습니다. 딱 우리의 목적과도 동일하네요. action 구간에 해당하는 attention weight를 키우고 background 구간에 해당하는 attention weight를 줄일 수 있다면 L1-regularization을 통해 sparsity 문제를 해결할 수 있습니다.
- $L_{s}=\frac{1}{B} \sum^{B}_{i=1} \parallel a_{i}\parallel_{1} $
이렇게 sparsity loss까지 알아보았습니다.
그래서 우리의 최종 Loss는 $L=L_{cls}+\alpha L_{d}+\beta L_{h}+\gamma L_{s}$ 입니다.
Experiments
실험에 대해서 알아보도록 하겠습니다. 실험 자체는 많지 않아 benchmarking이랑 ablation study 정도로 마무리가 됩니다. 실험 데이터셋은 temporal action localization에서 많이 사용하는 THUMOS'14와 ActivityNet을 사용했다고 합니다.
Comparison with state-of-the-arts methods
THUMOS'14
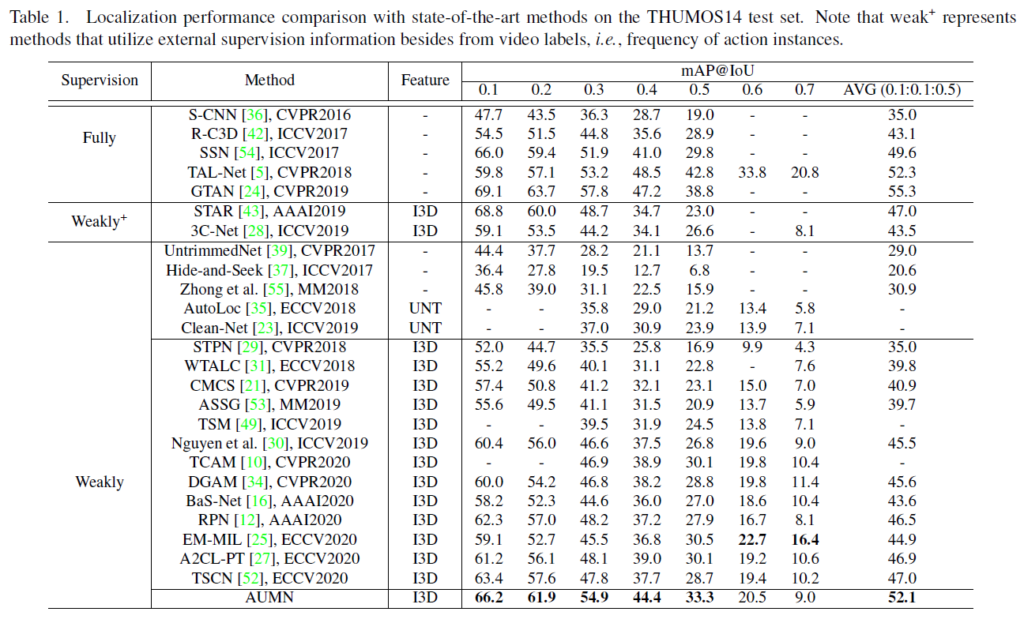
우선 제안된 AUMN 방법론이 Weakly-Supervised에서 꽤나 큰 폭으로 기존의 방법론들을 압살 하는 모습을 보여주고 있습니다.
ActivityNet
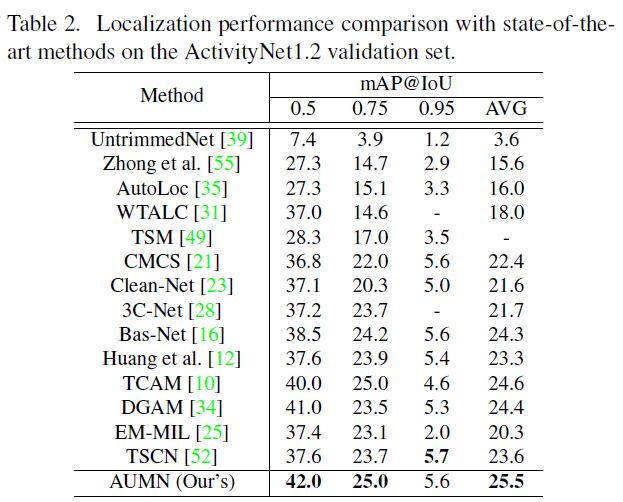
이제 ActivityNet에서의 성능인데 역시나 SOTA를 달성하고 있습니다. Temporal localization에서 두 가지 데이터셋(THUMOS'14와 ActivtyNet)에서 동일한 경향성을 보여주는 것은 다음을 의미합니다.
THUMOS'14는 Background Suppression이 중요한 데이터셋이고, ActivityNet은 Localization Completeness가 중요한 task입니다. 두 가지 데이터셋에서 SOTA라는 것은 둘 다 잘한다는 의미로 받아들이면 되겠죠.
Ablation Studies
Influence of Each Loss Function
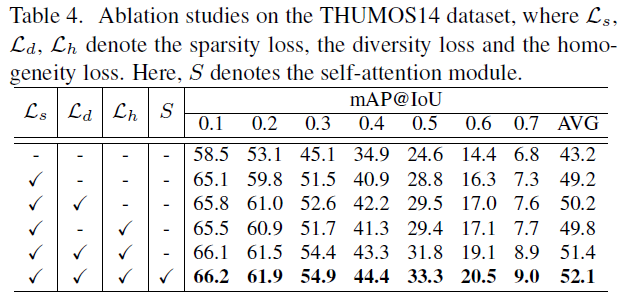
아까 방법론을 살펴볼 때 Memory bank를 업데이트하는 과정에서 classification loss만을 가지고 하는 것이 아니라 diversity, homogeniety, sparsity를 도입하여 memory bank의 다양한 특성들을 만족시킬 수 있게 하였습니다. 우선 $L_{s}$ sparsity Loss를 도입하면 mAP@avg 성능이 6이나 오르는 것을 확인할 수 있습니다. 사실상 sparsity에 대한 modeling이 localization 성능 기여에 일등공신이라 볼 수 있겠네요.
Sparsity Loss를 도입하면 action unit template들이 action과 연관된 segment에 집중을 하게 만드는 효과가 있기에 이러한 결과가 나왔다고 서술하고 있네요.
Diveristy Loss를 도입하지 않으면 template을 학습하는 데 있어 random initialization에 의존할 수밖에 없다고 하네요. 마지막으로 Homogeniety Loss를 도입하면 memory bank가 useless 해지는 것을 막을 수 있어 0.6의 성능 향상을 얻을 수 있었습니다. 모두 조합을 하면 가장 좋은 성능을 보여주고 있습니다.

또한 Self-Attention에 대한 ablation도 존재하는 데 self attention을 진행하는 것이 CAS를 좀 더 부드럽게 만들어주는 효과를 보여주고 있고 이로 인해 Localization 성능 향상을 꾀할 수 있었습니다.
Conclusion
이 논문의 가장 큰 contribution은 memory bank라는 것을 도입하여 Temporal action localization에서 발생하는 세 가지 특성들을 함께 modeling 하는 framework를 제안했다는 점에 있는 것 같습니다.
중간중간 template이라는 용어도 나오고 방법론이 조금 어려웠던 논문이어서 어찌어찌 겨우 읽은 것 같습니다.
LSTM에서 사용되는 개념을 가져다가 사용해 좋은 결과를 만들어낸 것을 봤을 때, 연구를 하기 위해서는 다양한 domain의 지식이 필요할 때도 있는 것 같습니다.
리뷰 읽어주셔서 감사합니다.



